2类变形Sierpinski地毯的Hausdorff维数

单家俊，龙伦海，杨　成，王司晨

(海南大学 信息科学技术学院,海南 海口 570228)



2类变形Sierpinski地毯的Hausdorff维数

单家俊，龙伦海，杨成，王司晨

(海南大学 信息科学技术学院,海南 海口 570228)

摘要：构造了圆心角小于180°的扇环与正方形之间的某种双Lipschitz映射，首先证明了若将经典Sierpinski地毯的初始图形正方形换成此类扇环，则得到的变形Sierpinski地毯与经典的Sierpinski地毯具有相同的Hausdorff维数；其次证明了若将初始图形换成圆心角小于180°的扇形，则其生成的变形Sierpinski地毯的Hausdorff维数也有同样的结果.

关键词：分形； 变形Sierpinski地毯；Hausdorff维数； 双Lipschitz映射

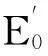
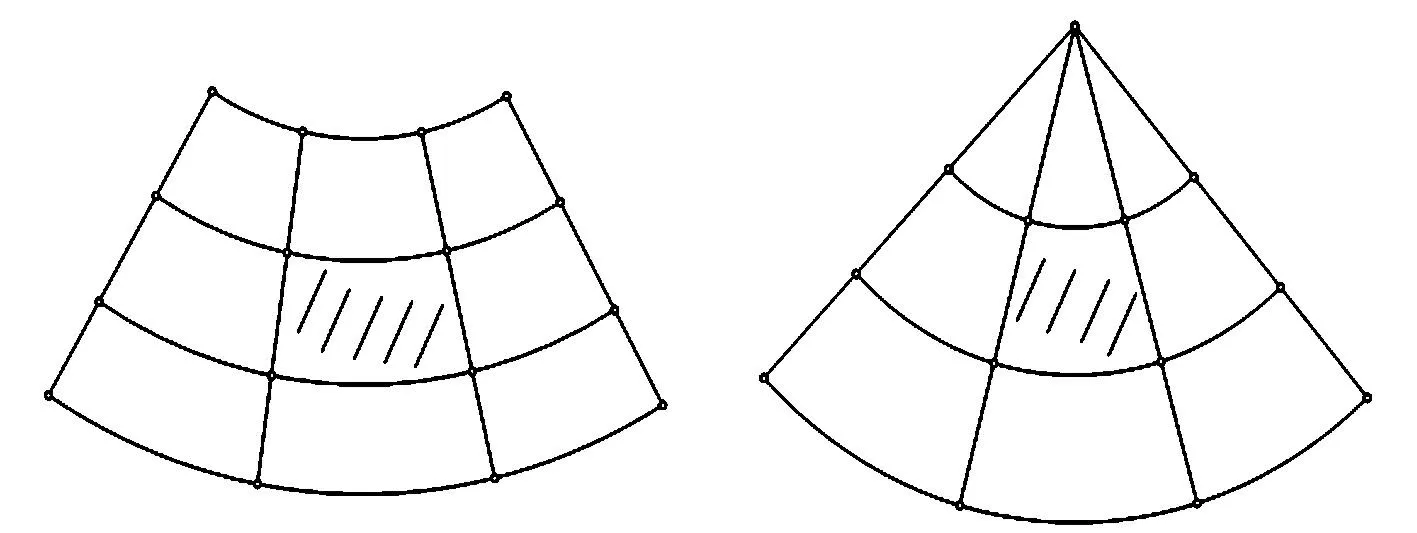
a　　　　　　　　　　　　　　　　　　　b图 1　圆心角小于180°的扇环和扇形

首先将其初始图形换成圆心角小于180°的扇环，利用定比分点构造了此类扇环与正方形之间的双Lipschitz映射，从而证明了此类变形Sierpinski地毯的Hausdorff维数是log8/log3. 在此基础上证明了如果将其初始图形换成圆心角小于180°的扇形，则得到的分形集的维数也为log8/log3. 本文主要结果如下：

定理1设E和E′分别为上述生成的变形Sierpinski地毯，则dimH(E)=dimH(E′)=log8/log3.

1预备知识

定义1设Rn中的任意非空子集E，{Ui}为E的一个有限或可数个直径不超过δ的覆盖，E⊆∪Ui，则称{Ui}为E的一个δ覆盖. 设s≥0，称

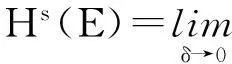
为E的Hausdorff测度，称

dimHE=sup{s:Hs(E)=∞}=inf{s:Hs(E)=0}

为E的Hausdorff维数.

C1·d(x1,x2)≤D(f(x1),f(x2))≤C2·d(x1,x2)

成立，则称f是双Lipschitz映射. 对于双Lipschitz映射，有以下引理成立：

引理1[1]如果f为双Lipschitz映射，则dimHE=dimHf(E).

平面上扇环和扇形中，利用定比分点计算容易得到以下性质.

对于平面上的三角形，有以下性质成立.

为了证明本文的结论，还需要用到以下不等式.

性质40≤λ≤1，0≤θ≤π，不等式1-cos(λθ)-λ2(1-cosθ)≥0成立.

证明令f(θ)=1-cos(λθ)-λ2(1-cosθ)，则

f′(θ)=λsin(λθ)-λ2sinθ，f″(θ)=λ2(cos(λθ)-cosθ).

因为函数y=cosx在[0,π]上是单调递减，0≤λ≤1，所以cos(λθ)-cosθ≥0,故f″(θ)≥0. 从而有f′(θ)在[0,π]上是单调递增，于是得到f′(θ)≥f′(0)=0，所以函数f(θ)在[0,π]上也单调递增，故f(θ)≥f(0)=0，不等式成立.

2定理1的证明

2.1E的Hausdorff维数根据引理1，如果能够构造一个双Lipschitz映射f，将正方形映射成扇环，且将由正方形分割生成的极限集映射为由扇环分割生成的极限集，则二者的Hausdorff维数相等. 下面构造双Lipschitz映射f.

定义映射f：f((λ1，λ2))=[λ1，λ2]. 显然映射f是双射，且对所有的0≤λ1，λ2≤1，f将正方形映射为扇环.

现在需要证明：1)映射f为双Lipschitz映射；2)映射f将由正方形分割生成的极限集映射为由扇环生成的极限集E.

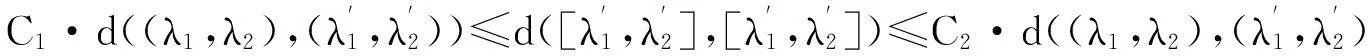
(1)

(2)

(3)

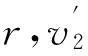
(4)

(5)

(6)

结合式(5)和(6)，故存在常数C1，C2>0，使得不等式

成立，于是f为双Lipschitz映射. 因为经典Sierpinski地毯的Hausdorff维数[1]为log 8/log 3，故由扇环分割得到的分形集E的Hausdorff维数也为log 8/log 3.

现在证明E′的Hausdorff维数也为log 8/log 3.

(7)

diam(Pk)≤2D03-k，diam(Qk)≤2D03-k.

又因为 ∀0<δ<1，存在k0，使得2D03-(k0-1)≤δ≤2D03-k0，根据Hausdorff维数的定义，有

令δ→0，得到Hlog 8/log 3(E′)≤(2D0)log 8/log 3，故dimH(E′)≤log 8/log 3.

另一方面，记Q=Q1∩E′，则由上节的讨论可知dimH(Q)=log 8/log 3，而Q⊂E′，再由Hausdorff维数的单调性，故有log 8/log 3=dimH(Q)≤dimH(E′)成立.

综合上述，dimH(E′)=log 8/log 3，定理1得证.

参考文献：

[1]FalconerKJ.Fractalgeometry-mathematicalfoundationsandapplications[M].[S.l.]:JohnWiley,2014.

[2]FalconerKJ.Fractalgeometry:mathematicalfoundationsandapplications[M].NewYork：JohnWilley&Sons,2003.

[3] 奚李峰. 从平面几何题中引申出的维数计算[C]//2006年分形几何与动力系统研讨会.乌鲁木齐:新疆师范大学,2006.

[4] 朱志勇,文志雄. 一类广义Sierpinski地毯的Huasdorff维数[J].应用数学,2011,24(2):360-365.

[5] 张贤达. 矩阵分析与应用[M].第2版.北京:清华大学出版社,2013:71-74.

[6]LlorenteM,MattilaP.Lipschitzequivalenceofsubsetsofself-conformalsets[J].Nonlinearity,2010,23:875-882.

[7] 朱莉红,陈绍明,龙伦海. 平面上广义McMullen集的Hausdorff维数[J].海南大学学报(自然科学版)，2012，30(4)：320-324.

[8]FengDJ,WenZY,WuJ.SomedimensionalresultsforhomogeneousMoransets[J].ScienceofChina:SeriesA,1997,40(5):475-482.

[9]GuiYX,LiWX.TheHausdorffdimensionofsetsrelatedtothegeneralSierpinskicarpets[J].ActamathematicaSinica,EnglishSeries,2010,26(4):731-742.

[10] 龙伦海,梁丽,朱莉红.由点矩阵的表示生成的分形矩阵的维数[J].数学进展，2015,44(2):229-238.

Hausdorff Dimension of Two Classes of Modified Sierpinski Carpets

Shan Jiajun, Long Lunhai, Yang Cheng，Wang Sichen

(CollegeofInformationScienceandTechnology,HainanUniversity,Haikou570228,China)

Abstravct：Inthereport,abiLipschitzmapbetweensquareandsectorringwhosecentralanglewaslessthan180°wasconstructed.Firstly,itwasprovedthatifwechangetheinitialsetofSierpinskicarpetfromsquaretosectorring,theHausdorffdimensionareequal.Secondly,itwasalsoshowedthattheHausdorffdimensionoftheModifiedSierpinskicarpetremainthesameeventheinitialsetisreplacedintothesectorwhosecentralangleislessthan180°.

Keywords：fractals;McMullenset;Hausdorffdimension;bi-Lipschitzmap

收稿日期：2015-06-29

基金项目：国家自然科学基金(11461016)；海南省自然科学基金 (113003)

作者简介：单家俊(1992—)，男，江西南昌人，海南大学2013级硕士研究生，研究方向：分形几何及其应用，E-mail:15501863129@163.com 通信作者： 龙伦海(1965—)，男，教授，研究方向：分形几何，E-mail：13118900189@163.com

文章编号：1004-1729(2016)01-0007-05

中图分类号：O174.12

文献标志码：ADOl：10.15886/j.cnki.hdxbzkb.2016.0002