CBFM：支持属性删减的布鲁姆过滤器矩阵多维元素查询算法

王勇，云晓春,2，王树鹏，王曦



CBFM：支持属性删减的布鲁姆过滤器矩阵多维元素查询算法

王勇1，云晓春1,2，王树鹏1，王曦1

（1. 中国科学院信息工程研究所北京 100093；2. 国家计算机网络应急技术处理协调中心北京 100029）

为了提升多维元素成员查询的灵活性和准确率，提出了一种新型索引结构CBFM(cutted Bloom filter matrix)。该索引方法通过独立属性布鲁姆过滤器笛卡尔乘积构建位矩阵，支持任意属性组合的多维元素成员查询，同时支持属性组合按需删减和属性加权，极大地提升内存空间利用率，降低查询误判率。理论分析证明相比于BFM(Bloom filter matrix)索引方法，CBFM具有更高的内存利用率。仿真实验表明，在分配内存相同的情况下，CBFM方法相比于其他方法，具有最低的查询误判率，特别在内存受限场景下，CBFM相比于BFM方法，查询误判率最大降低3个数量级，极大地提升了多维元素成员查询的准确率。

查询算法；多维元素成员查询；布鲁姆过滤器；位矩阵

1 引言

随着移动互联网、Web2.0等相关产业的快速发展，数据逐渐呈现出规模巨大化、类型多样化、流量高速化等大数据[1]特征，数据多维特征日趋明显，海量多维数据的存储、计算及实时分析为信息系统带来严峻的挑战。多维元素成员查询，是一种判断特定对象是否存在于目标数据集的重要手段，在数据集上进行全维度或部分维度查询并得到true/false的回答，广泛应用于分布式云存储[2~6]、网络监控及测量[7]等系统中。

在分布式云存储系统中，面对PB级数据量、数万属性的数据管理需求，Google BigTable[2]、HBase[3]等云存储系统，在进行数据操作之前，都需要在分布式节点上进行成员查询以便于定位目标数据；在MapReduce[4]、Hive[5]、Impala[6]等并行计算系统中，通过多维元素成员查询，可以实现本地分区多维数据块的快速存在性检测，极大地降低本地分区数据块的磁盘扫描时间，提升查询效率。在网络监控及测量应用中，由于TCP协议超时重传及路由器可能的故障重复转发等原因，大量重复数据产生，导致在其之上的数据查询及分析不可信，通过多维元素成员查询，可以有效地进行网络流数据重复检测等预处理[7]，以便实现高效的网络传输及在线数据分析。

多维元素成员查询典型解决方案包括表索引[8,9]、树索引[10,11]及布鲁姆过滤器[12]索引结构。其中，表索引[8, 9]将多维元素存在于表中，其最大缺点是内存占用较高；树索引结构[10,11]能够支持元素查询的多维性，但是其面向异构数据集的结构负载均衡难度较大，而且应用集成复杂性较高；布鲁姆过滤器[12]是一种可以高效表示数据集合并进行存在性判断的数据结构，其核心优点是具备较高的空间效率和查询效率，但其不支持任意属性组合查询，MDBF[13]、CMDBF[14]对布鲁姆过滤器进行了多维扩展，但是其针对支持任意属性组合的元素成员查询存在较高的误判率，尤其对于属性相关性较高的数据集表现并不理想；BFM算法[14]是目前较为经典的布鲁姆过滤器多维扩展方法，支持任意属性组合多维元素成员查询，查询误判率也相对较低，但是其内存利用率较低，且无法支持属性权重的差异化处理。综上所述，多维元素成员查询的核心技术在于多维索引的构建，其应该具备查询模式自由(schema-free)能力，即支持任意属性组合的元素成员查询，同时应具备较高的内存空间利用率、较低的查询误判率和属性权重差异化处理能力。

本文提出了一种新型索引结构CBFM（cutted Bloom filter matrix），该索引方法通过独立属性布鲁姆过滤器笛卡尔乘积构建位矩阵，支持任意属性组合的多维元素成员查询，同时支持属性组合按需删减和属性加权，极大地提升内存空间利用率，降低查询误判率。本文的贡献可以归纳为如下内容。

1) 结合多维元素成员查询的相关研究现状，给出此问题的形式化定义，并在此基础上，提出了一种新型索引结构CBFM，CBFM支持任意属性组合的多维元素成员查询，并通过属性组合按需删减和属性加权的方式提升内存空间利用率，降低查询误判率。

2) 理论分析证明了CBFM索引方法的内存空间高效性。相比于BFM索引方法，CBFM在期望误判率一致的前提下，通过维度删减的方式大幅降低内存空间占用。

3) 针对CBFM方法进行了充分的仿真实验，在查询误判率、内存空间占用、维度扩展性等方面与相关研究工作进行充分比较，实验数据表明，在分配内存相同的情况下，CBFM具有最低的查询误判率，特别在内存受限场景下，CBFM相比于BFM，查询误判率最大降低3个数量级。同时CBFM具备较好的维度扩展能力。

2 相关研究工作

多维元素成员查询典型解决方案包括表索引、树索引及布鲁姆过滤器索引结构，其中，布鲁姆过滤器以其较高的空间利用率及查询性能等优势应用较广，下面首先介绍布鲁姆过滤器及其多维扩展。

2.1 布鲁姆过滤器

标准布鲁姆过滤器[12]SBF由一个位向量和一组散列函数构成，如图1所示。假设数据集合总计个元素，所有元素均通过个散列函数映射到长度为的位向量中。当进行元素插入时，对于每一个元素，计算，将置位为1；当进行元素查询时，对于给定元素，检查位向量的个位置，若所有位置均判断为1，则判定可能在集合中，否则一定不在集合中。

综上所述，标准布鲁姆过滤器存在一定的假阳性概率(false positive rate)，即不属于集合中的元素可能被判定为属于此集合。

2.2 布鲁姆过滤器多维扩展

标准布鲁姆过滤器SBF不支持多维元素成员查询，Guo等[13]提出了一种多维布鲁姆过滤器算法MDBF，算法核心思想是针对多维数据集的每一个属性，构建独立的布鲁姆过滤器，当查询元素时，通过判断多维元素的各个属性值是否都存在于相应的布鲁姆过滤器，来判断元素是否属于集合。CMDBF[14]在MDBF基础上新增一个用于表示元素整体的联合布鲁姆过滤器CBF，并将元素表示和查找分2步进行，将MDBF各属性的表示和查询作为第1步，第2步联合元素所有属性域，利用CBF完成元素整体的表示和查询确认。在配置参数为{,,,}情况下，CMDBF查询误判率为，略低于MDBF查询误判率。

MDBF、CMDBF均未能有效解决多维元素成员查询场景下的任意属性组合查询问题，文献[14]提出了一种布鲁姆过滤器矩阵算法(BFM)，该算法在每个维度上保存一个位向量以构建布鲁姆过滤器，并基于独立属性笛卡尔乘积构建位矩阵，用于全属性组合查询，从根本上消除了组合误差率；同时，BFM在独立属性位向量上添加1个标记位，以支持任意属性组合查询。实验证明BFM索引方法在高相关性数据集场景下，具备相对较低的查询误判率，是目前应用较广的多维元素成员查询算法。然而，随着数据集维度数的增加，算法内存空间占用呈指数级增长，且查询误判率会随所查询属性数目减少而大幅提升。

与文献[15]不同，文献[16]提出了布鲁姆过滤器笛卡尔联接索引算法(CBF)，该索引方法仅存储全属性位矩阵信息，不维护特殊标记位，在非完整属性集上采用遍历的方法，因此其内存空间利用率稍好于BFM方法，但是在任意属性组合查询及查询效率方面略显不足。

2.3 其他相关研究工作

除布鲁姆过滤器及其多维扩展外，多维元素成员查询典型解决方案包括表索引[8,9]、树索引[10,11]及混合索引[18,19]结构等。

文献[8]提出一种应用于ZFS分布式文件系统的表索引方案，将多维元素存储于表中以实现成员查询，其最大的不足是内存占用偏高，而且查询复杂度较高（或）；紧凑型散列表[9]可以在一定程度上提升查询效率，并降低内存占用，但同时固化了查询模式。

在树索引研究方面，Zhou等[10]提出了一种双层索引算法EDMI，算法核心思想如下：全局索引层采用KD树进行子空间划分，局部索引层针对每个子空间，采用ZPR树进行数据索引。MD-HBase[11]提出了一种基于空间目标排序的多维索引算法，其核心思想是采用Z排序技术对多维空间目标进行排序，以Z-Value作为每条记录的键值，并在此基础上利用KD树或四叉树对多维数据空间进行划分，并计算各子空间最长公共前缀作为索引项，以支持数据内容查询。树结构索引算法较好地解决了元素查询的多维性，但是其空间复杂度较高，而且结构负载不均对整体查询性能存在较大影响。

目前广泛应用的混合索引结构是将布鲁姆过滤器与树索引进行融合。Adina等[18]在2015年提出了一种混合索引结构Bloofi，将B+树和布鲁姆过滤器进行层次化融合，并在此基础上实现位级别的并行化算法Flat-Bloofi，有效解决了多维数据集的元素查询问题。为了解决云存储环境下的非KEY字段查询问题，BF-Matrix[19]提出了一种层次化索引结构，结合了布鲁姆过滤器和B+树，极大缩减了元素查询路径，并采用基于规则的索引更新机制，有效降低布鲁姆过滤器的假阴性概率。

3 CBFM设计

3.1 形式化定义

本文在上述研究工作的基础上给出了多维元素成员查询的形式化定义。假设数据集合总计个元素，其中，任一数据项均为多维对象,由个不同属性构成,即。

基于应用场景差异，多维元素成员查询支持2种查询模式。针对全属性查询模式，查询元素内容；任意属性组合查询模式，查询元素内容。多维元素成员查询返回true/ false的结果，返回true；返回false。

3.2 CBFM算法

CBFM索引方法，通过独立属性布鲁姆过滤器笛卡尔乘积构建位矩阵，支持任意属性组合的多维元素成员查询，同时支持属性组合按需删减和属性加权，极大的提升内存空间利用率，降低查询误判率。其相关运行参数如表1所示。

表1 CBFM运行参数

为了保证多维元素成员查询场景下属性值的完整性，CBFM在每个属性上均采用一个独立的位向量，并采用位矩阵存储所有属性关联信息，极大地降低了组合误差率；同时支持删减不需要的属性组合，提升内存空间利用率。索引结构如图2所示。

由图2(a)所示，CBFM在不删减属性组合情况下，与BFM索引方法一致，保存一个全属性矩阵；图2(b)显示了删减属性组合的结构，二维矩阵和三维矩阵的存储空间被极大地释放，同时不影响所有单属性及其他属性组合的成员查询。图3给出了CBFM插入一个二维元素(A, A)的示意。

CBFM索引结构在默认情况下，所有属性权重相等，位向量大小保持一致。为了更好地支持多维元素成员查询场景下属性权重的差异性，CBFM可以扩展为加权模型（WCBFM-Weighted CBFM），即可以针对重要属性或属性组合，分配相对较大的内存空间，进一步降低查询误判率。

CBFM多维元素插入算法流程如图4所示。新元素插入时，首先拆分多维元素的各属性值，采用散列函数进行置位计算；其次，针对每个散列函数，联合各属性值的散列置位结果值，计算位矩阵逻辑下标；然后，基于已删减属性组合信息，将逻辑下标转换为实际位矩阵下标；最后在CBFM中进行置位，完成数据插入。

算法1 elementInsert(Object Element)输入:待插入的多维元素A=(a1,a2,…,ad)输出:VOIDbeginassign 0 to ResultArray;for each attribute ax in A { for each hashFunction hashx in HashSet { record hashx(ax) to hashPerField[][];} //针对每个属性计算k次散列} //end forfor each DC of (2d−1) combinations { for each hash value hashV in hashPerField { //调用calculateIndex计算实际索引下标 invoke calculateIndex(DC, hashV, ResultArray);}} //end for//采用实际索引下标对位数组进行置1处理for each idx of ResultArray { set bit of ResultArray [idx] to 1} //end forend elementInsert

CBFM多维元素成员查询算法流程如图5所示。对于待查询多维属性组合，如果其中包含已删减属性组合，需要进行拆分查询。本算法采用迭代的方式进行属性拆分。

算法2 elementSearch(Object Element)输入:待查询的多维元素A=(a1,a2,…,ad), 其对应维度组合SDC，非必选字段值为null输出:元素是否存在beginassign 0 to ResultArray;for each field ax in A { for each hashFunction hashx in HashSet { record hashx(ax) to hashPerField[][];} //针对每个属性计算k次散列} //end forfor each EDC(does not match any dimension combinations to cut off) of SDC { for each hash value hashV in hashPerField { //调用calculateIndex计算实际索引下标 invoke calculateIndex(EDC, hashV, ResultArray);}} //end forfor each idx of ResultArray { if bit of ResultArray [idx] equals to 0 { return FALSE;}} //end forreturn TRUE;end elementSearch

3.3 模型复杂度分析

根据布鲁姆过滤器基本原理得知，假设散列取值服从均匀分布，当集合中所有元素都映射完毕后，查询误判率为[17]

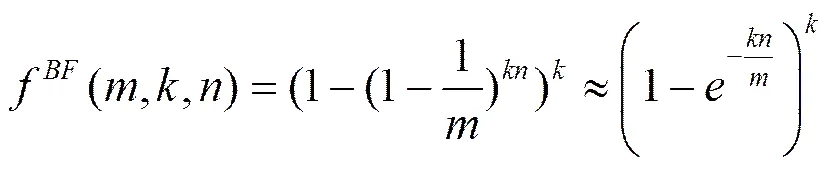
假设期望误判率和期望元素数已经固定，在此基础上计算散列函数个数和位向量的最优解为

(2)

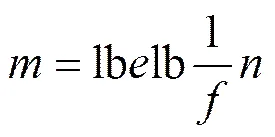
因此，CBFM实际位向量大小如式(4)所示，相比于BFM索引方法的内存空间占用m，具备相对较低的内存占用。

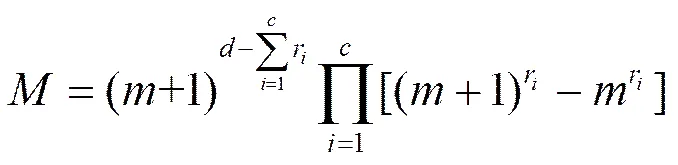
当进行多维元素成员查询时，针对待查询维元素，CBFM算法首先应用个散列函数对非空字段进行散列计算，次数上限为；其次，算法根据个已删减维度组合将待查询维度进行拆分，最多得到个非重复维度组合，针对每个查询维度组合信息，算法由高到低遍历其中每一个维度，通过枚举相对删减维度组合，计算当前维度中特殊标记位与非特殊标记位中的实际位个数（如图6所示），运算次数上限为，综上所述，CBFM元素查询时间复杂度上限为。在实际应用中，维度数和散列函数个数都是确定的，算法的查询时间复杂度为常数，而且与数据集大小之间并无相关性。

算法3 calculateIndex(Object DC, Object hashV, Object ResultArray)输入:插入元素A=(a1,a2,…,ad)的一种维度组合; 使用某散列函数计算出每个字段的散列值数组; 需要置位的位索引数组输出:VOIDbeginif DC match some dimension combinations to cut off { end calculateIndex; //维度组合与删减组合一致}assign 0 to currentBitIndex;//由高位至低位遍历DC中的每个维度信息for each dimension ax in DC(from high to low) { //将ax按照特殊位和非特殊位独立处理 split ax to special bit array and normal bits array; calculate non-bulk offset in special bit array, and add it to currentBitIndex;calculate non-bulk offset in normal bits array, and add offset*(hashV[ax]−1) to currentBitIndex;} //end foradd currentBitIndex to ResultArray;end calculateIndex

3.4 数值示例

表2和表3给出二组数值示例，它们分别对比了BFM和CBFM算法，随着期望误判率的变化，期望元素数和期望内存空间占用的变化趋势。在表2中，预设总可用内存大小为1 MB，期望误判率从10−1变化到10−5，在三维数据集场景下，CBFM删减2个两属性组合(0x5代表删减维度1、3；0x3代表删减维度1、2)，CBFM期望元素个数始终是BFM的14倍以上，这也预示着CBFM在查询误判率上的优势。在表3中，期望插入元素数=1 000，CBFM内存占用比BFM低3个数量级以上，间接反映了CBFM索引方法具备相对较高的内存空间利用率。

表2 期望元素数量对比(M=1 MB)

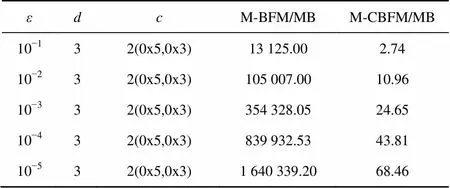
表3 期望内存空间占用对比(n=1 000)

4 仿真实验

本节通过仿真实验测试CBFM索引结构在不同属性组合场景下的查询误判率、查询效率、内存空间占用等核心指标，并与SBF、MDBF、CMDBF、BFM、CBF等索引算法进行比较。

4.1 查询误判率

本文分别在全属性查询、两属性查询场景下，对比了SBF[12]、MDBF[13]、CMDBF[14]、CBF[15]、BFM[16]、CBFM这6种索引结构，其中，CBFM索引结构删减了一个两属性组合。

实验1 构造数据集验证查询误判率

在实验中，采用三维布鲁姆过滤器阵列，当数据插入时，每一属性值均采用独立的数据集合，其值为计算机随机构造出的32位无符号整数，取值范围为{0,232−1}。在进行多维元素成员查询时，首先确保所有待查询多维数据与已存储数据集不重复；同时，为了体现所查询数据与插入数据的相关性，本文定义了一个相关性系数，用来表示查询数据集中重复元素的占比，因此意味着查询数据集任一字段与插入数据集均无重叠，意味着查询数据集所有字段均来自插入数据集。

为了公平对比，本文在上述6种索引结构中设置了相同的散列函数个数(=6)及内存空间大小(=16 MB)。由图7(a)可以看出，在全属性查询模式下，SBF、BFM、CBFM、CBF索引方法具有较低的查询误判率，CMDBF、MDBF在相关系数逐渐增大的过程中，误判率持续增大。尤其在相关性系数=1情况下，SBF、BFM、CBFM、CBF等索引算法的误判率相比与CMDBF、MDBF等方法的误判率低了3个数量级，这是因为SBF、BFM、CBFM、CBF更好地解决了组合误差率问题。MDBF方法由于不能解决组合误差率问题，因此随着相关系数增大，误判率渐趋近于1。

由于SBF、CMDBF不支持两属性查询，针对MDBF、BFM、CBFM、CBF进行了误判率实验。由图7(b)可以看出，BFM、CBF误判率为最高100%，CBFM误判率最低(约为0.21%)，相比于BFM方法低了3个数量级。这是因为CBFM删减了2个属性组合，相比于BFM具有更大的内存空间存储待查询属性组合信息，CBFM在内存受限场景下的适应性更强，空间利用率相对更高。

实验2 根据实际数据集验证查询误判率

为了进一步验证CBFM算法的有效性，本节采用实际数据进行测试，数据源来自运营商DNS协议通信流量，核心测试属性为{源IP地址，目的IP地址，域名}三元组信息。在数据插入和查询环节，分别采用真实数据集不同时间区间的流量数据。

图8(a)展示了随着可用内存空间变化，全属性查询误判率的变化趋势。与合成数据集测试结果类似，全属性查询模式下，SBF、CBFM仍然保持相对较低的误判率，BFM算法由于存在较高的空间需求导致其位冲突率较高进而增大了误判率。在两属性查询模式下，本文采用{源IP地址，域名}属性组合，由图8(b)可以看出，CBFM查询误判率最低，相比于其他算法，其具备更高的内存空间利用率。

实验3 属性加权查询误判率测试

为了验证属性加权对于查询误判率的影响，本文针对三维度数据集下，在实验1基础上提升2个属性存储权重，降低第3个属性存储权重，总存储空间不变，得到的测试结果如图9所示。

由图9可以看出，WCBFM（加权CBFM）在全属性查询、两属性查询场景下，查询误判率均相对较低，全属性查询模式下误判率降低约1.69倍，两属性组合查询模式下误判率降低2个数量级。加权CBFM索引方法为特定系统应用优化提供了更大的便利，可以按照应用需求进行属性权重指定。

4.2 查询效率

在进行查询误判率实验的同时，本文记录了查询过程中的耗时情况，具体实验结果如图10所示。

由图10可以看出，CBFM索引方法的查询耗时是BFM、MDBF、CBF等索引方法的2~3倍，这是由于在CBFM查询过程中，需要针对删减属性进行查询优化，将原有查询拆分为多次查询，此性能损失可以通过算法并行化进行优化解决，也是本文的下一步工作方向之一。

4.3 内存空间占用

为了验证CBFM索引方法的内存高效性，本文在维度数={1,2,3,4}，单维期望元素数=100，期望误判率=0.1场景下进行算法内存空间占用对比实验。

图11给出了CBFM理论内存占用、CBFM实际内存占用（CBFM在维度数等于3、4情况下删减一个两属性组合）、BFM实际内存空间占用的对比测试结果。可以看出，CBFM内存空间占用理论值和实际值基本一致，这也验证了理论分析的正确性。当维度数为1情况下，理论值与实际值的差距主要是由于程序内部变量所占内存空间导致。在实际内存空间占用对比方面，随着维度数增大，BFM、CBFM方法占用内存均持续增加，但BFM内存空间增加趋势更加明显，特别是在维度数为4的场景下，BFM内存空间占用比CBFM方法高了2个数量级左右。

4.4 维度扩展性

图12给出了在任意属性组合查询场景下，维度数与查询效率之间的关系。实验采用三维度数据集，单维度数组大小为16位，测试了维度数从2增长到8的过程。

CBFM算法查询效率并没有随着维度数增加而线性增长，这更加有利于CBFM在高维数据集上的应用。同时，随着插入数据集逐渐增大，特定维度查询效率基本保持稳定，这也验证了CBFM算法查询复杂度与插入数据集并无相关性。

5 结束语

多维元素成员查询在分布式云存储、网络流量分析等系统中具有重要的应用意义，其核心挑战在于多维索引结构的设计，支持全属性及任意属性组合成员查询，同时具备较低的查询误判率和内存空间占用。为了提升多维元素成员查询的灵活性和准确率，本文详细分析了SBF[12]、MDBF[13]、CMDBF[14]、CBF[15]、BFM[16]等5种多维索引方法，并在此基础上提出了一种新型索引结构CBFM(Cutted Bloom Filter Matrix)，该索引方法通过独立属性布鲁姆过滤器笛卡尔乘积构建位矩阵，支持任意属性组合的多维元素成员查询，同时支持属性组合按需删减和属性加权，提升内存空间利用率，降低查询误判率。本文详细分析了CBFM索引结构的模型复杂度，并给出算法进行多维元素插入和成员查询的工作流程。与此同时，本文从查询误判率、查询效率、维度扩展性等多个角度进行了索引结构的验证工作，实验证明，相比于现有方法，CBFM具备相对更低的查询误判率，并具备较好的维度扩展性。

本文的下一步工作方向可以归纳为两点。首先，目前主流的多维索引结构均假设所有属性权重一致，本文虽然在多维元素成员查询的属性加权方面进行了初探，但是如何基于属性差异化权重，实现属性相应布鲁姆过滤器的参数化调整策略仍是未来主要的工作方向；其次，如何分析多维查询和数据集的相关性，并在已知数据集特征场景下进行算法适应性优化也是本文一项重要的工作内容。

[1] LYNCH C. Big data: how do your data grow[J]. Nature, 2008, 455(7209): 28-29.

[2] CHANG F, DEAN J, GHEMAWAT S, et al. Bigtable: a distributed storage system for structured data[J]. ACM Transactions on Computer Systems (TOCS), 2008, 26(2): 4.

[3] VORA M N. Hadoop-HBase for large-scale data[J]. IEEE Computer Science and Network Technology, 2011, (1): 601-605.

[4] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113.

[5] THUSOO A, SARMA J S, JAIN N, et al. Hive: a warehousing solution over a map-reduce framework[J]. Proceedings of the VLDB Endowment, 2009, 2(2): 1626-1629.

[6] KORNACKER M, BEHM A, BITTORF V, et al. Impala: a modern, open-source SQL engine for Hadoop[C]. Conference on Innovative Data Systems Research (CIDR'15). c2015.

[7] TARKOMA S, ROTHENBERG C E, LAGERSPETZ E. Theory and practice of bloom filters for distributed systems[J]. Communications Surveys & Tutorials, IEEE, 2012, 14(1): 131-155.

[8] RODEH O, TEPERMAN A. zFS-a scalable distributed file system using object disks[C]//Mass Storage Systems and Technologies (MSST), c2003: 207-218.

[9] DEBNATH B, SENGUPTA S, LI J. FlashStore: high throughput persistent key-value store[J]. Proceedings of the VLDB Endowment, 2010, 3(1-2): 1414-1425.

[10] ZHOU X, ZHANG X, WANG Y, et al. Efficient distributed multi-dimensional index for big data management[M]. Springer Berlin Heidelberg, 2013. 130-141.

[11] NISHIMURA S, DAS S, AGRAWAL D, et al. MD-HBase: a scalable multi-dimensional data infrastructure for location aware services[J]. IEEE Mobile Data Management (MDM), 2011, 1: 7-16.

[12] BLOOM B H. Space/time trade-offs in hash coding with allowable errors[J]. Communications of the ACM, 1970, 13(7): 422-426.

[13] GUO D, WU J, CHEN H, et al. Theory and network applications of dynamic bloom filters[C]//INFOCOM. c2006: 1-12.

[14] 谢鲲, 秦拯, 文吉刚, 等. 联合多维布鲁姆过滤器查询算法[J]. 通信学报, 2008, 29(1): 56-64.

XIE K, QIN Z, WEN J G, et al.Combine multi-dimension Bloom filter for membership queries[J]. Journal on Communications，2008，29( 1) : 56-64.

[15] WANG Z, LUO T, XU G, et al. A new indexing technique for supporting by-attribute membership query of multidimensional data[M]. Springer Berlin Heidelberg, 2013. 266-277.

[16] WANG Z, LUO T, XU G, et al. The application of cartesian-join of bloom filters to supporting membership query of multidimensional data[C]//IEEE Big Data. c2014: 288-295.

[17] BRODER A, MITZENMACHER M. Network applications of bloom filters: a survey[J]. Internet Mathematics, 2004, 1(4): 485-509.

[18] CHENG X, LI H, WANG Y, et al. BF-matrix: a secondary index for the cloud storage[M]. Springer International Publishing, 2014. 384-396.

[19] CRAINICEANU A, LEMIRE D. Bloofi: multidimensional Bloom filters[J]. Information Systems, 2015, 54: 311-324.

CBFM：cutted Bloom filter matrix for multi-dimensional membership query

WANG Yong1, YUN Xiao-chun1,2, WANG Shu-peng1, WANG Xi1

(1.Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China; 2. National Computer Network Emergency Response Technical Team/Coordination Center of China, Beijing 100029, China)

In order to improve the flexibility and accuracy of multi-dimensional membership query, a new indexing structure called CBFM(cutted Bloom filter matrix) was proposed. CBFM built the bit matrix by the Cartesian product of different bloom filters, each representing one attribute of primary data. In this way, the proposed matrix supported by-attribute membership query. Besides, the attribute combinations in the bit matrix could be reduced and weighted on demand to further enhance memory utilization rate. Theoretical analysis proves that CBFM utilizes memory more efficiently than BFM, the current state of art. Experiments also show that, on the scenario of memory size fixed, the false positive rate of CBFM is lower than that of all other indexing methods. Especially on the scenario of memory constrained, the false positive rate of CBFM can be 3 orders of magnitude lower than that of BFM(Bloom filter matrix) indexing method. CBFM is an accurate data structure for multi-dimensional membership query.

query algorithm, multi-dimensional membership query, Bloom filter, bit matrix

TP393

A

10.11959/j.issn.1000-436x.2016061

2015-08-16；

2015-12-04

国家自然科学基金资助项目（No.61271275, No.61501457, No.61202067, No.61303261）；国家高技术研究发展计划(“863”计划)基金资助项目（No.2012AA013001, No.2013AA013205, No.2013AA01A213）

The National Natural Science Foundation of China (No.61271275, No.61501457, No.61202067, No.61303261), The National High Technology Research and Development Program of China (863 Program) (No.2012AA013001, No.2013AA013205, No.2013AA01A213)

王勇（1985-），男，黑龙江双鸭山人，中国科学院信息工程研究所博士生，主要研究方向为海量数据存储、网络安全。

云晓春（1971-），男，黑龙江哈尔滨人，博士，中国科学院信息工程研究所研究员、博士生导师，主要研究方向为网络信息安全。

王树鹏（1980-），男，山东济南人，博士，中国科学院信息工程研究所副研究员，主要研究方向为海量数据存储、网络安全。

王曦（1985-），女，黑龙江哈尔滨人，中国科学院信息工程研究所助理研究员，主要研究方向为网络安全。