基于DInSAR技术与断层自动剖分方法反演断层滑动参数

陈丹蕾， 刘国祥， 王晓文， 王蕾， 蒲慧龙

(1.四川省第三测绘工程院，成都　610500； 2.西南交通大学地球科学与环境工程学院，成都　610031)



基于DInSAR技术与断层自动剖分方法反演断层滑动参数

陈丹蕾1， 刘国祥2， 王晓文2， 王蕾1， 蒲慧龙1

(1.四川省第三测绘工程院，成都610500； 2.西南交通大学地球科学与环境工程学院，成都610031)

摘要：以合成孔径雷达差分干涉测量(DInSAR)技术获得的同震形变数据为约束，基于弹性位错模型反演获得发震断层的几何、运动参数(也称滑动参数)，对于了解震区断层活动特征和评估潜在灾害风险具有重要意义。现有的断层滑动参数反演多是基于矩形位错元的均匀剖分或人为设定剖分，所得结果易出现“伪滑动”和滑动分布过于平滑的问题，不足以精确地反映断层面上的滑动细节。为此，引入断层自动剖分方法。该方法兼顾了模型残差最小化与平滑最优原则，在形变数据的有效约束下获得可靠解。以巴姆地震为例反演获得断层的几何参数与滑动参数。实验结果表明，对于单断层的滑动参数反演，应用断层自动剖分方法可获得较可靠的结果。

关键词：断层自动剖分；DInSAR； 滑动参数反演； 混合采样

0引言

利用合成孔径雷达干涉测量技术(interferometricsyntheticapertureRadar,InSAR)可以快速获取震区地表连续覆盖的同震形变信息[1-4]，通过在InSAR形变数据与地下断层参数之间建立模型并进行解算，可获得发震断层的几何参数和滑动参数，这对于研究地震的发震机理和了解震区的断层活动特征具有重要意义。断层的滑动参数反映了断层的运动情况，为了构建精细的断层滑动模型，可将断层剖分为许多个小位错元，并细化至求解每个位错元上的滑动值。常规的滑动参数反演大都基于矩形面源模型[2-4]，采用均匀剖分[5]和人为设定剖分[6]。然而，矩形位错元在模拟复杂几何模型时易在断层连接处出现间隙和重叠现象，并且很难实现连续光滑曲面断层的模拟。若使用三角形位错元则可避免上述问题，实现任意形状曲面的模拟，适用于复杂断层[7-8]。在对断层面进行离散剖分时，若采用均匀剖分或人为设定剖分反演得到的滑动分布常会出现滑动分布过于平滑，无法表现真实的精细分布特征； 或者在某些位置上的滑动分布太过细化，呈现出一些基于数据本身无法完全确定的滑动(伪滑动)特征[7]。

针对以上问题，引入断层自动剖分方法[9]，基于尺寸可变的三角形位错单元，以反演模型分辨率最优为原则迭代得到最佳断层位错元尺寸，将滑动合理地分布到所有位错元上，并以巴姆地震为例，应用断层自动剖分方法获得断层的滑动分布解。

1断层自动剖分原理

1.1模型参数求解

依据地表形变数据与断层参数之间的关系，断层参数的反演可分为几何参数的非线性反演和滑动参数的线性反演，统一用式(1)表示，即

G(m)=d ,

(1)

式中：G为格林函数矩阵，由均匀弹性半空间位错模型[10]获得； m为断层参数； d为地表形变观测值。

在反演求解参数的过程中常采用正则化算法，即通过引入附加信息来解决方程病态问题或避免过度拟合现象的产生[11]，这些附加信息通常是平滑约束信息或解空间的边界约束条件。本文采用高阶Tikhonov正则化算法求解m，权衡考虑了误差最小化和解的平滑性，通过附加正则化条件的残差二范式，即

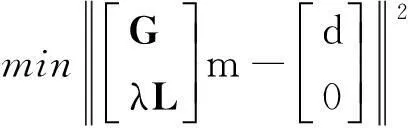
(2)

来获得残差最小时对应的模型解m。式中：L为拉普拉斯平滑矩阵，用以克服邻近位错元上的剧烈滑动梯度变化，避免解振荡的产生； λ是正则化权参数，若其值过大，会滤掉很多有用的观测值，造成模型的过度平滑; 其值过小，则会混入过多噪声，致使拟合模型中混入不可靠信息，偏离真实情况。一个合适的正则化权参数既能平滑噪声，又能避免模型的过度拟合。本文采用jRi的方法[9]获得正则化权参数，jRi的值反映了反演质量的优劣,其值越小，代表当下断层剖分越合理，取jRi最小值赋给λ。jRi的表达式为

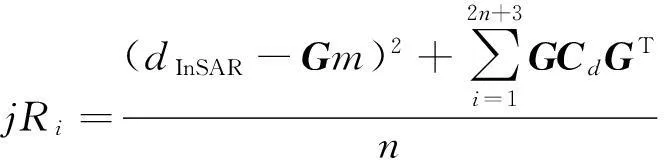
(3)

式中： Cd为观测值的方差—协方差矩阵；n为观测数。求得λ值后便可计算广义逆矩阵G-g，即

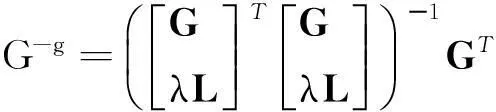
(4)

在已知G，λ和L的前提下，可利用正则化方法以最小二乘为约束，求得m的初始分布模型。

1.2自动剖分

断层自动剖分方法是利用模型分辨率矩阵拟合产生所有位错元的最佳尺寸，从而对初始位错元的大小进行调节，使滑动在位错元上合理分布的过程。自动剖分流程如图1所示。

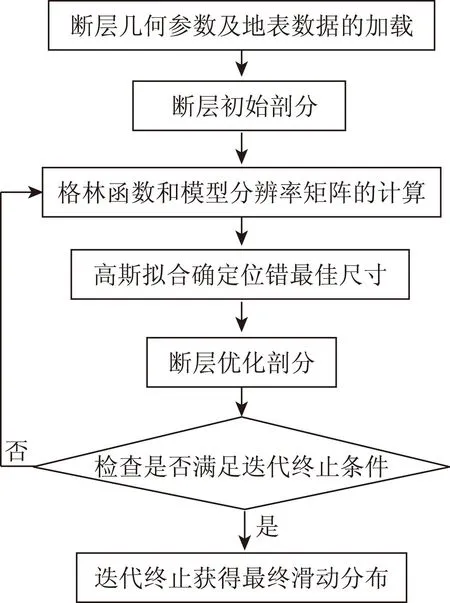
图1　断层自动剖分流程

断层自动剖分的具体步骤包括数据的加载、断层的初始剖分、正则化格林函数和模型分辨率矩阵的计算、最佳位错尺寸的确定、断层优化剖分和迭代收敛检验。

1.2.1模型分辨率矩阵的计算

模型分辨率矩阵R是与位错中心位置和地表形变观测数据质量有关的一个参数矩阵，它的行元素代表净滑动值在相关断层片中的平滑程度[12]，可以由

R=G-gG

(5)

予以确定。根据矩阵R可以判断位错元上的滑动是伪滑动，还是不足以表现细节的粗略滑动分布，继而通过产生新的位错剖分来更好地反映数据的解析能力。

1.2.2最佳位错尺寸的确定

初始滑动分布确定后，需要基于数据的解析能力，对位错尺寸进行可变剖分。为了使断层模型中每个位错元上的滑动都是基于数据的有力约束，需要在位错尺寸与滑动分布的平滑尺度之间建立函数对应关系，通过高斯曲线拟合，建立模型分辨率矩阵R的第i行元素(表示第i个位错元上的滑动在所有位错元上的平滑程度)与位错尺寸之间的高斯函数关系，如图2所示。

图2　高斯拟合获得最佳位错尺寸

拟合得到的高斯函数的宽度设定为平滑尺度，将其大小作为位错的尺寸，此时滑动在各个位错元上的分布接近狄克拉函数，对应的断层剖分是最佳剖分。比较平滑尺度与位错尺寸，如果平滑尺度接近当前位错元的大小，该位错元的剖分就比较适宜； 如果平滑尺度大于或小于位错尺寸，那么位错元的剖分就不正确，需要对位错尺寸进行调节。

1.2.3迭代终止条件

以相邻2次迭代所得位错元总数的差异百分数作为标准，即如果在某次迭代后，新增加或减少的位错元数目的百分比在容许范围内，则终止迭代，否则将继续进行迭代计算，直至满足迭代条件为止。

2同震形变场获取与数据降采样

2.1同震形变场的获取

利用SAR影像对的干涉处理结果可获取巴姆地震的同震形变信息。本实验选用2幅覆盖同一震区范围的降轨影像组成干涉对，其参数如表1所示。

表1　干涉对参数及基线估计

由主、从影像对干涉处理及差分干涉处理得到震区干涉相位图及同震形变图(图3和图4)。

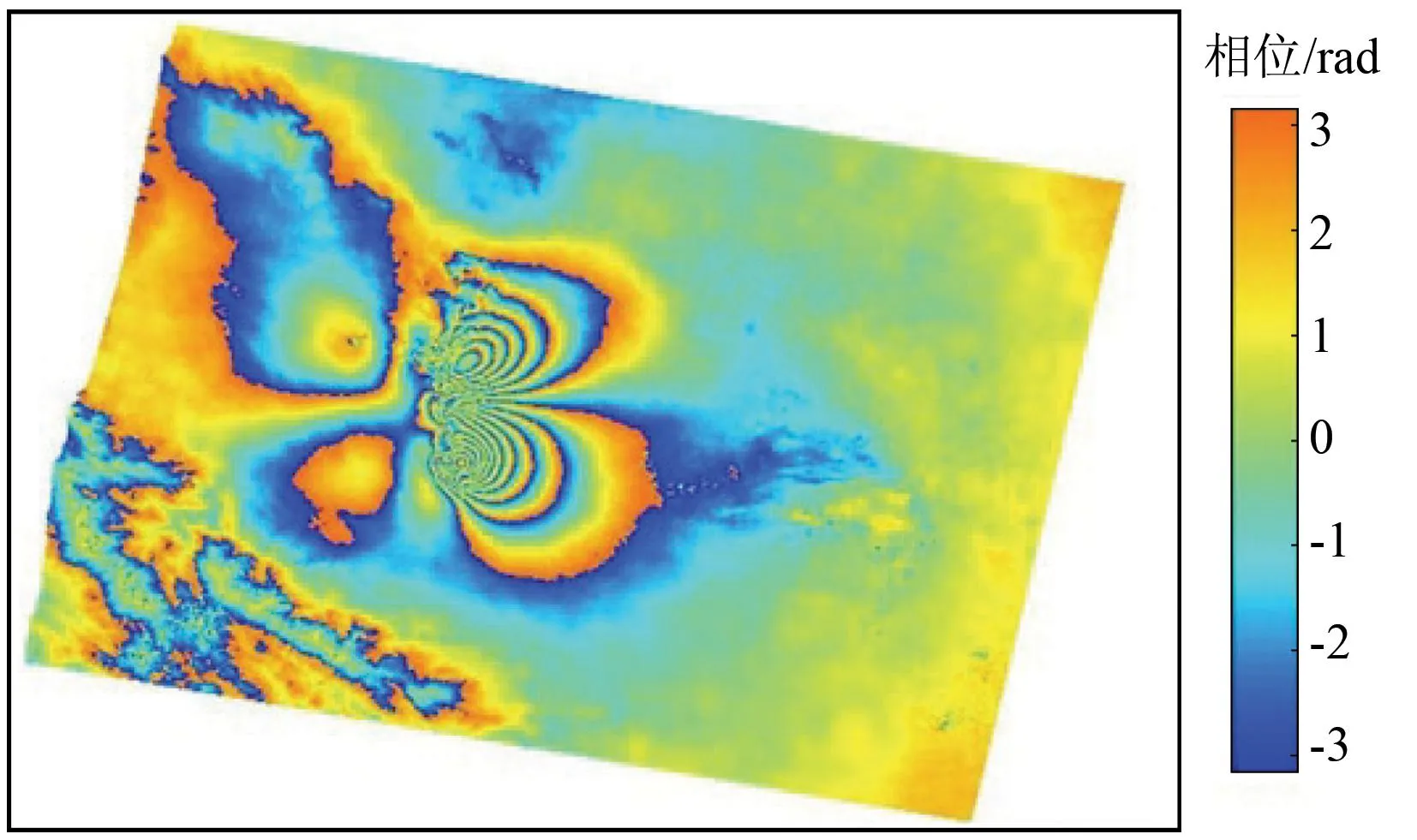
图3　巴姆地震干涉相位图

图4　巴姆地震同震形变图

图4的雷达视线向形变图中一个颜色周期代表了2π的相位变化，对应的地表形变值为2.8 cm，整个震区的形变范围在-16.82～30.33 cm之间。地表形变集中分布在巴姆城市的东北侧和东南侧，东北侧以地表沉降为主，东南侧以地面抬升为主。西北侧有2～4 cm的下降，西南侧有少量抬升，其值在2 cm左右。

2.2数据降采样

为保证反演迭代收敛和提高解算速率，需要对数量庞大的形变数据进行降采样。鉴于四叉树降采样法可以较好地保留原始数据的分布特征[3-4]，本文首先利用四叉树采样方法对原始形变数据进行降采样，其结果如图5所示。

(a) 四叉树采样后的形变场 (b) 采样点分布 (c) 残差分布

图5四叉树采样结果

Fig.5Results of quadtree resampling

由图5可以看出，四叉树采样方法虽然可以较好地保持原始数据的分布特征，但在影像西南侧受山体叠掩引起的失相干部分也提取到了相当数量的采样点，若让这些数据参与后续的断层参数反演将会影响反演精度。基于以上考虑，本文采取混合采样方法，对西南侧受山体叠掩影响的远场区采用均匀采样，而对形变比较剧烈的近场区采用四叉树降采样。远场区和近场区是以整体形变量绝对值的平均作为阈值进行划分的。这样的采样方式既可以满足保留原始数据特征的要求，又可以避免远场区精度较差数据的干扰。

采用混合采样方法，将形变数据由6 236 235个降采样至1 736个，这些样点密集地分布在原始形变图中形变较大的区域，而其他区域的数据分布均匀且相对稀少，采样点分布情况如图6(b)所示。降采样前后，残差较大的地方出现在图像的顶部位置，误差约为4～5 cm，由于其范围较小不会对反演结果产生太大影响，故可予以忽略； 其他地方数据的误差都在0值附近，经计算残差的均方根误差为1.06 cm，残差分布如图6(c)所示。

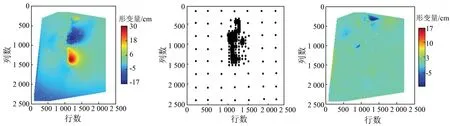
(a) 混合采样后的形变场(b) 采样点分布 (c) 残差分布

图6混合采样结果

Fig.6Results of mixed resampling

3反演实验

3.1断层几何参数的非线性反演

几何参数的反演是滑动参数反演的基础。本文对巴姆地震断层的几何参数反演是基于Okada[13]弹性半空间位错理论，利用Levenberg-Marquardt(LM)最小二乘优化算法迭代产生最优解。Okada弹性半空间位错理论为模型提供了联系待求参数与InSAR形变数据之间的格林函数，而LM优化算法是在最小二乘算法基础上附加阻尼因子，从而在解空间中搜索得到残差最小时的几何参数最优解，即寻求真实形变量与模型解算的模拟形变量之间的残差最小时对应的模型参数解。得到的几何参数作为滑动分布反演部分的输入参数，结果如表2所示。

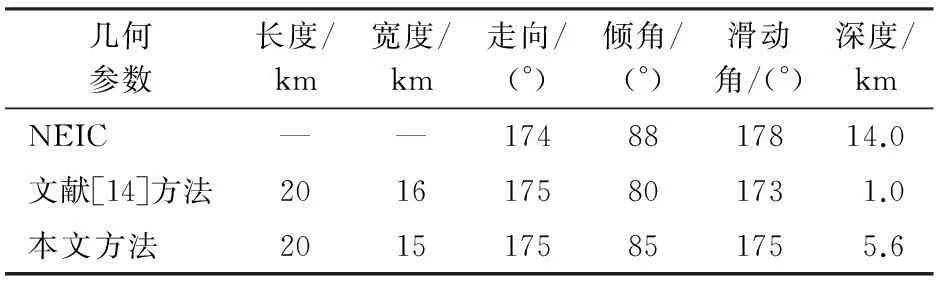
表2　断层几何参数反演结果

根据所得断层几何参数反演结果，并结合已有资料，初步确定巴姆地震是由隐伏单断层的右旋走滑运动(滑动角接近180°)为主引起的。为进一步求得断层面上的精细滑动分布情况，需要将断层面离散剖分为三角形位错元，并求得每个位错元上的滑动分布情况，本文采用断层自动剖分方法实现。

3.2断层滑动参数的反演

基于断层自动剖分的反演过程分为2部分： 一是基于均匀弹性半空间三角位错模型获得格林函数表达式，并通过正则化优化算法求得滑动解； 另一部分是断层自动剖分过程，通过高斯拟合计算获得所有位错元的最佳尺寸以及滑动在所有位错元的平滑程度情况，从而对当前的位错元尺寸和平滑尺度进行调节，迭代直至满足终止条件为止，产生的滑动分布如图7和图8所示。

图7　断层滑动平面分布

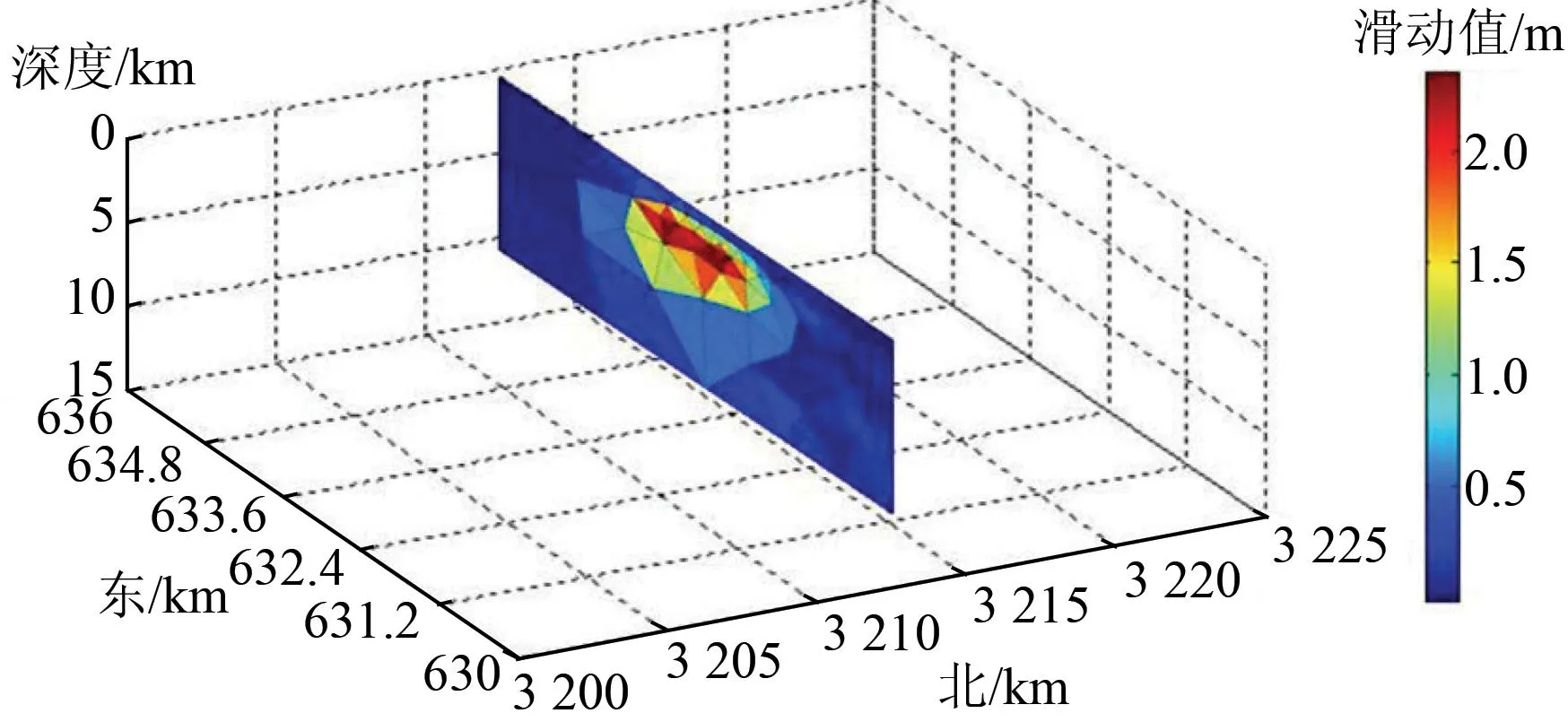
图8　断层滑动的地下空间分布

利用断层自动剖分方法将引发巴姆地震的右旋走滑断层剖分为151个大小不一的三角形位错元，每个位错元上对应不同的滑动值。总体滑动值分布在0.2～2.35 m之间，集中分布于地下0.5～11 km范围内，最大滑动值为2.35 m，出现在地下4.8 km处，平均滑动值为1.8 m。尺寸较小的三角形位错元分布在距离地表较近的地方，该区域滑动变化梯度较大，较小尺寸的位错元能够精细地反映滑动的变化情况； 而尺寸较大的三角形位错元分布在离地表较远的断层深处，滑动变化比较平缓，这反映了三角形可变剖分模型的平滑特征。

3.3结果分析与评价

为了评价反演所得发震断层参数的精度，需要通过正演解算获得模拟形变图，即由断层参数和格林函数求得模拟形变数据，并计算模拟形变量与真实形变之间的残差情况，以此为依据分析反演效果。模型残差可由式(6)获得，即

ε=G(m)-d，

(6)

式中ε表示残差。将断层参数作为已知数据，正演获得巴姆震区的模拟形变如图9所示。

图9　LOS向模拟形变

模拟形变与原形变干涉分布特征相似，形变集中区域可分为4个象限，形变分布情况与真实形变较吻合，但东南侧形变在25～30 cm之间的区域比真实形变范围略大，分析是由模拟数据内插至原始InSAR数据量级的过程中产生的误差所致。总体模拟形变范围为-16.45～34.16 cm之间，与真实形变范围接近，残差的均方根误差值为0.97 cm。如图10所示，由断层自动剖分方法反演所得的模型残差分布于-3.2～6.4 cm之间，整体残差以0为中心呈正态分布。

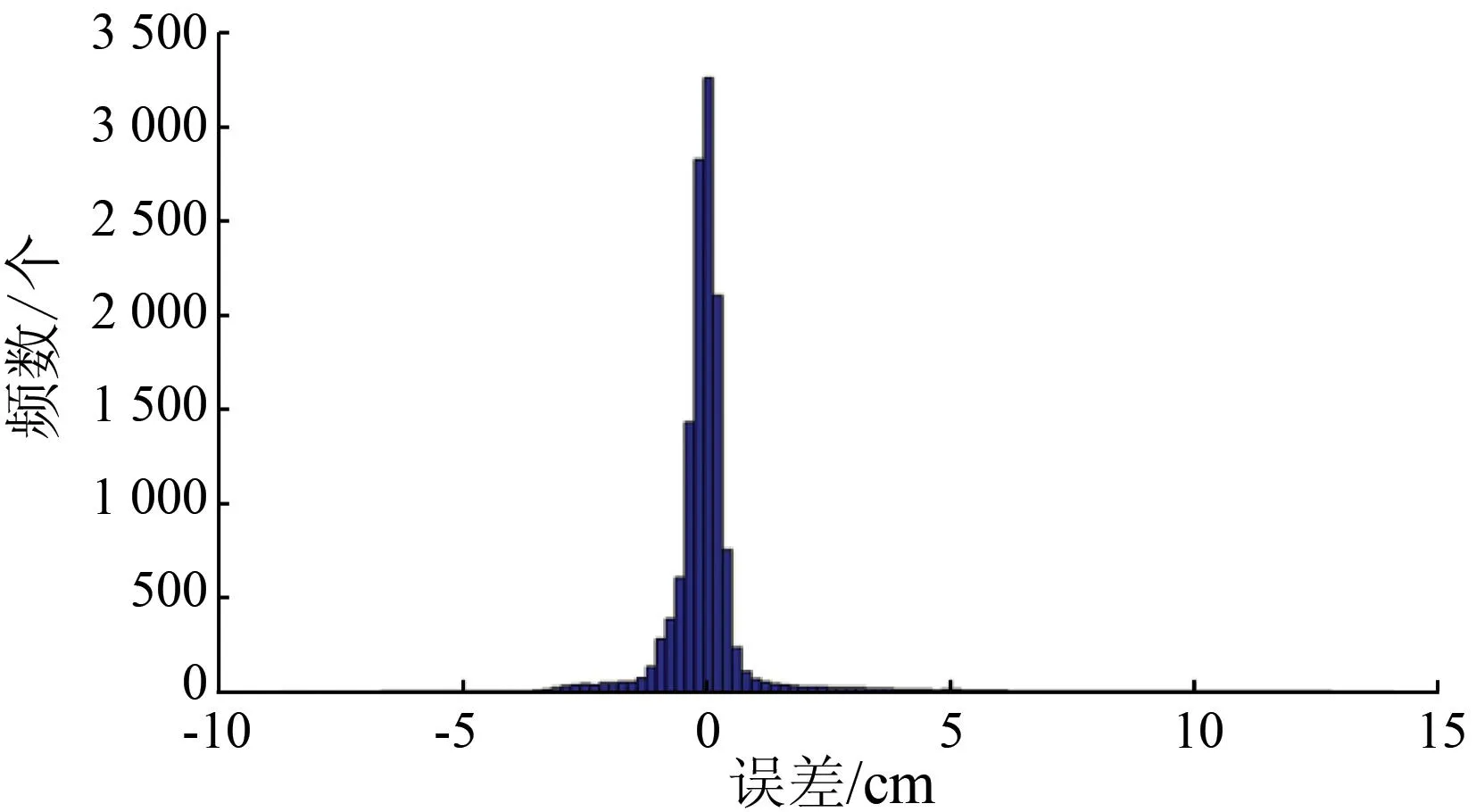
图10　反演结果的误差分布直方图

4结论

1)本文引入断层自动剖分方法，以巴姆地震为例，对发震断层的滑动参数进行反演，并通过正演比较模拟形变量与InSAR真实形变之间的残差，表明利用断层自动剖分方法对浅源单断层进行反演可获得较可靠滑动参数解。

2)利用断层自动剖分方法可以兼顾残差最小化和模型平滑性原则，避免了均匀剖分或人为设定剖分引起的“伪滑动”或滑动过于平滑的现象，提高解的可靠性。

3)本文仍存在一些不足之处。对于浅源单断层引起的地震，断层自动剖分方法可以反演获得较可靠的滑动参数解，但对于震级较高且发震断层构造较复杂的地震，该方法是否适用还有待于进一步研究论证； 地震反演结果的精度评价一直是该领域长期存在的普遍性问题，仅通过正演模拟进行残差比较具有一定的局限性，也有待于开展进一步研究。

参考文献(References)：

[1]洪顺英,申旭辉,单新建,等.基于升降轨ASAR的于田Ms 7.3级地震同震形变场信息提取与分析[J].国土资源遥感,2010,22(4):98-102.doi:10.6046/gtzyyg.2010.04.20.

Hong S Y,Shen X H,Shan X J,et al.The calculation and analysis of the co-seismic deformation field of Yutian Ms 7.3 earthquake basing on the ascending and descending orbit ASAR data[J].Remote Sensing for Land and Resource,2010,22(4):98-102.doi:10.6046/gtzyyg.2010.04.20.

[2]罗旭巍,孙建宝,沈正康,等.基于InSAR同震形变观测反演2010年新西兰南岛Mw7.1 Darfield地震同震破裂分布[J].地球物理学报,2013,56(8):2613-2624.

Luo X W,Sun J B,Shen Z K,et al.Co-seismic slip distribution of 2010 Darfield, New Zealand Mw7.1 earthquake inverted using InSAR measurements[J].Chinese Journal of Geophysics,2013,56(8):2613-2624.

[3]薛莲,孙建宝,沈正康.2010年1月12日海地Mw7.0级地震InSAR同震形变观测及同震滑动分布反演[J].地震地质,2011,33(1):157-174.

Xue L,Sun J B,Shen Z K.InSAR coseismic deformation observation of the Jan 12th, 2010 HaiTi earthquake and its coseismic slip distribution inversion[J].Seismology and Geology,2011,33(1):157-174.

[4]周辉,冯光财,李志伟,等.利用InSAR资料反演缅甸Mw6.8地震断层滑动分布[J].地球物理学报,2013,56(9):3011-3021.

Zhou H,Feng G C,Li Z W,et al.The fault slip distribution of the Myanmar Mw6.8 earthquake inferred from InSAR measurements[J].Chinese Journal of Geophysics,2013,56(9):3011-3021.

[5]温扬茂,何平,许才军,等.联合Envisat和ALOS卫星影像确定L’Aquila地震震源机制[J].地球物理学报,2012,55(1):53-65.

Wen Y M,He P,Xu C J,et al.Source parameters of the 2009 L’Aquila earthquake, Italy from Envisat and ALOS satellite SAR images[J].Chinese Journal of Geophysics,2012,55(1):53-65.

[6]Resor P G,Pollard D D,Wright T J,et al.Integrating high-precision aftershock locations and geodetic observations to model coseismic deformation associated with the 1995 Kozani-Grevena earthquake,Greece[J].Journal of Geophysical Research:Solid earth,2005,110(B9):B09402.

[7]Walters R J,Elliott J R,D’Agostino N,et al.The 2009 L’Aquila earthquake(central Italy):A source mechanism and implications for seismic hazard[J].Geophysical Research Letters,2009,36(17):L17312.

[8]张国宏,屈春燕,汪驰升,等.基于GPS和InSAR反演汶川Mw7.9地震断层滑动分布[J].大地测量与地球动力学,2010,30(4):19-24.

Zhang G H,Qu C Y,Wang C S,et al.Inversion of slip distribution of 2008 Wenchuan Mw7.9 earthquake constrained jointly by InSAR and GPS measurements[J].Journal of Geodesy and Geodynamics,2010,30(4):19-24.

[9]Barnhart W D,Lohman R B.Automated fault model discretization for inversions for coseismic slip distributions[J].Journal of Geophysical Research,2010,115(B10):B10419.

[10]Meade B J.Algorithms for the calculation of exact displacements,strains, and stresses for triangular dislocation elements in a uniform elastic half space[J].Computer and Geosciences,2007,33(8):1064-1075.

[11]Golub G H,Hansen P C,O’Leary D P.Tikhonov regularization and total least squares[J].SIAM Journal on Matrix Analysis and Applications,1999,21(1):185-194.

[12]Du Y J,Aydin A,Segall P.Comparison of various inversion techniques as applied to the determination of a geophysical deformation model for the 1983 Borah Peak earthquake[J].Bulletin of the Seismological Society of America,1992,82(4):1840-1866.

[13]Okada Y.Surface deformation due to shear and tensile faults in a half-space[J].Bulletin of the Seismological Society of America,1985,75(4):1135-1154.

[14]凌勇,曾祺明,罗扬,等.巴姆地震变形场和应力场:I.用差分干涉雷达和Okada方法求解[J].岩石学报,2006,22(9):2367-2374.

Ling Y,Zeng Q M,Luo Y,et al.Deformation and stress field of Bam earthquake:Ⅰ.InSAR and Okada calculation[J].Acta Petrologica Sinica,2006,22(9):2367-2374.

(责任编辑： 陈理)

Inversion of fault slip parameters based on DInSAR and automated fault model discretization method

CHEN Danlei1, LIU Guoxiang2, WANG Xiaowen2, WANG Lei1, PU Huilong1

(1. The Third Engineering Institution of Surveying and Mapping of Sichuan, Chengdu 610500, China; 2. Faculty of GeosciencesandEnvironmentalEngineering,SourthwestJiaotongUniversity,Chengdu610031,China)

Abstract:The inversion of geometry and motion parameters of the seismogenic fault based on elastic dislocation model and constrained by coseismic deformation data obtained by DInSAR has great significance for understanding the activity characteristics of the fault and assessing the risk of potential disasters. The existing inversion methods of fault slip parameters are mostly based on the uniform discretization with rectangular dislocation units or artificially setting discretizaiton, which will lead to “pseudo-slip” or the phenomenon that the slip distribution is too smooth to reflect the slip details on the fault plane. Therefore, the automated fault model discetization method is introduced in this paper, which takes into account the principle of the minimized residuals and the optimal smoothing scales of the model, so the reliable solution can be obtained under the effective constraints. The inversion of geometry and slip parameters of fault in Bam earthquake is taken as an example. The experimental results show that using the automated fault model discretization method to invert the motion parameters of the single fault can generate reliable results.

Keywords:automated fault model discretization； DInSAR； inversion of slip parameters； mixed resampling

doi:10.6046/gtzyyg.2016.03.05

收稿日期：2015-02-02；

修订日期：2015-03-20

基金项目：四川省测绘地理信息局科技计划项目 “基于Web的四川省地理国情监测数据成果展示方法与实现”(编号：J2014ZC16)资助。

中图法分类号：TP79

文献标志码：A

文章编号：1001-070X(2016)03-0025-06

第一作者简介：陈丹蕾(1987-)，女，硕士研究生，助理工程师，主要从事InSAR技术应用与遥感应用等方面的科研工作。Email: 281560206@qq.com。

引用格式： 陈丹蕾，刘国祥，王晓文,等.基于DInSAR技术与断层自动剖分方法反演断层滑动参数[J].国土资源遥感,2016,28(3):25-30.(ChenDL,LiuGX,WangXW,etal.InversionoffaultslipparametersbasedonDInSARandautomatedfaultmodeldiscretizationmethod[J].RemoteSensingforLandandResources,2016,28(3):25-30.)