基于同轨约束RFM的高分卫星影像区域网平差

潘红播， 邹峥嵘， 张过， 张云生， 汪韬阳

(1.中南大学地球科学与信息物理学院,长沙　410083； 2.武汉大学测绘遥感信息工程国家重点实验室,武汉　430079； 3.武汉大学遥感信息工程学院,武汉　430079)



基于同轨约束RFM的高分卫星影像区域网平差

潘红播1， 邹峥嵘1， 张过2， 张云生1， 汪韬阳3

(1.中南大学地球科学与信息物理学院,长沙410083； 2.武汉大学测绘遥感信息工程国家重点实验室,武汉430079； 3.武汉大学遥感信息工程学院,武汉430079)

摘要：高分辨率光学(简称“高分”)卫星影像普遍以标准景的形式提供给用户，并附带有理多项式模型(rational function model,RFM)。尽管同一轨道高分影像的姿态和轨道误差较为稳定，然而由于RFM的参数没有清晰的物理意义，因此难以建立同一轨道影像间的几何约束关系。从条带影像与标准景影像的差异出发，考虑标准景影像的分景效应以及积分时间差异的影响，提出了基于像方多项式模型的同轨约束方法，可对同轨道、不连续的标准景影像进行约束，实现基于同轨约束的高分卫星影像区域网平差。通过用我国资源三号(ZY-3)测绘卫星同轨7景三线阵立体影像和印度IRS-P5卫星两轨4景两线阵立体影像进行实验，证明所提出的同轨约束区域网平差模型能减少对控制点的需求，提高平差精度。

关键词：高分卫星影像； 同轨约束； 区域网平差； 有理多项式模型(RFM)

0引言

高分辨率光学(简称“高分”)卫星影像是基础地理信息的重要数据源，被广泛应用于测图和地理国情普查等方面。然而，在卫星影像获取过程中，卫星的姿态、轨道参数不可避免地带有测量误差，需要利用控制点提高影像的定位精度。由于控制点的获取比较困难、周期长、成本高，成为制约生产效率的关键因素； 因此对于大区域的应用，减少区域网平差对控制点数目的需求显得尤为迫切[1]。在传统航空摄影测量中，因影像视场角较大，相邻景影像间可以构成空中三角锁，故在航线首末处使用4个控制点即可实现航带影像的绝对定向[2]。然而，对于高分卫星影像来说，由于其视场角较小，所以无法构建类似的空间三角锁航线。王任享[2]针对这一问题，在假设每个取样时刻外方位元素独立的前提下，提出了用等效片法求解三线阵影像等效片时刻的外方位元素，并通过外方位元素连续平滑的约束条件实现高分影像的区域网平差； 但该方法还需获取影像的严格成像几何参数。另一种解决条带影像区域网平差的方法是： 假设高分影像外方位元素误差较为稳定，采用低阶多项式模型的方法，通过少量控制点实现对误差模型的求解[3-6]。

有理多项式模型(rational function model,RFM)是一种通用传感器模型，其参数缺乏物理意义，往往采用像方或物方的多项式模型进行区域网平差[7-9]； 但这种平差模型无法建立参数与姿态和轨道误差的几何关系，因而无法建立相邻景影像间的几何约束。当对同一轨道的标准景影像进行区域网平差时，因其求解参数较多、参数相关等因素，故导致少量控制点难以实现高精度区域网平差[10]。张力等[1]在我国西部测图工程中，通过计算整轨影像的RFM，实现了稀少控制点的区域网平差。张过等[11]通过对同一轨道影像构建新的条带影像，重新计算了条带影像的成像几何模型。但上述2种方法均无法解决中间景缺失时的条带重建问题，且补偿格网模型的形式较为复杂。

本文从高分卫星影像基础产品的制作原理出发，分析标准景影像与条带影像产品之间的几何约束关系，建立同一轨道影像间的几何约束，实现基于同轨约束的高分卫星影像区域网平差。通过用我国资源三号(ZY-3)测绘卫星同轨7景三线阵立体影像和印度IRS-P5卫星两轨4景立体影像进行验证的结果表明，本文提出的方法能减少对控制点的需求，实现高精度区域网平差。

1基于RFM的区域网平差

RFM作为一种通用的、与传感器无关的遥感影像几何模型，已被广泛应用于摄影测量处理系统中。当前高分卫星影像普遍提供RFM作为成像几何模型(如WorldView3，GF-1等)。RFM的形式为

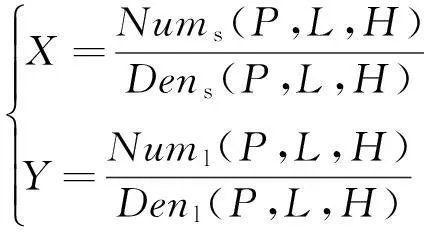
(1)

式中：Nums(P,L,H)，Dens(P,L,H)，Numl(P,L,H)和Denl(P,L,H)分别为归一化物方坐标(P,L,H)的三次多项式模型；X,Y为归一化像方坐标。归一化方程为

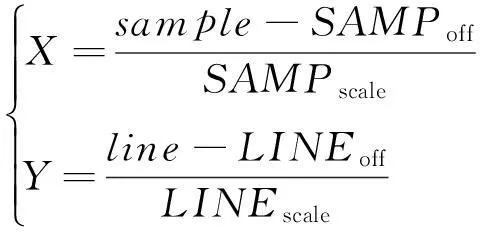
(2)

式中：LINEscale，LINEoff，SAMPscale和SAMPoff分别为像方坐标的归一化参数；line和sample分别为图像量测的行坐标与列坐标。

由于RFM的参数不再含有物理意义，因此无法建立姿态误差(包括平台姿态误差和安装角误差)、轨道误差与RFM参数之间的几何关系。Grodecki等[7]考虑到高分辨率线推扫式影像的姿态误差和轨道误差之间高度相关，且其误差可通过像方多项式模型吸收，故建立补偿模型，即

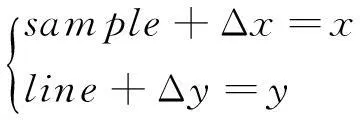
(3)

式中： (x,y)为RFM计算得到的像方坐标； (Δx, Δy)为像方多项式补偿模型，其形式为

(4)

式中a0,a1,a2,…和b0,b1,b2,…为模型精化参数。当参数仅为前3项时，该补偿模型为常用的像方仿射变换模型。利用1个控制点可以求解偏移参数(a0和b0)，这样几乎可以吸收大部分误差； 利用2个控制点则可同时求解平移和漂移量(a0,a1,b0和b1)[9]。

对于条带影像来说，由于其平台较为稳定，姿态误差和轨道误差可用时间的低阶多项式模型表示； 因此，基于RFM的长条带影像区域网平差即使在少量控制点的情况下，也可以达到亚像元级的定位精度[7, 10, 12]。

2基于同轨约束的平差模型

当前，高分卫星影像产品普遍以标准景的形式提供给用户。在现有区域网平差方法中，标准景影像之间并没有建立起有效的几何约束关系。本文将构建标准景影像与条带影像间的几何约束关系，以条带为平差单元，建立同轨约束的RFM高分卫星影像区域网平差模型。

对于摄影测量的几何处理来说，用户倾向于使用传感器校正产品[13]，因为该产品较好地保留了成像时的几何关系。为向用户提供易于使用的基础影像产品，传感器校正产品采用虚拟重成像技术，消除了影像中的内外畸变，且附带高替代精度的RFM。内畸变消除是通过虚拟电荷耦合器件(charge-coupled device,CCD)重成像实现的，具有以下特点： ①不考虑镜头畸变，为理想小孔成像； ②位于焦平面上的单组CCD； ③像元大小相同，等间隔分布； ④虚拟CCD覆盖各片CCD的成像范围。虚拟CCD通过检校的内方位元素计算得到，对于同轨影像来说，其内方位元素将保持不变； 而外畸变消除的过程包括积分时间规划、姿态滤波和轨道滤波3部分。

为了保证时间延迟积分(time delay and integration,TDI)CCD的积分速度与像移速度一致，TDI CCD的积分时间随地面纬度变化[14]。由于高分卫星的轨道采用近圆形轨道，可认为其线速度近似相等，故积分时间变化将造成影像沿轨向的分辨率发生变化。积分时间规划是消除影像内因积分时间不一致造成的影像内部的几何畸变； 姿态滤波是为了消除姿态抖动引起RFM替代精度降低； 轨道滤波则是为了消除轨道噪声的影响。姿态滤波和轨道滤波过程引起的光线方向变化将引入高程误差，这种误差在传感器校正产品制作过程中得到了控制，因此可以认为相邻景重叠区域的成像光线仍然保持平行。在考虑到相邻景影像积分时间可能存在差异时，相邻景影像像点坐标应满足如下约束关系，即

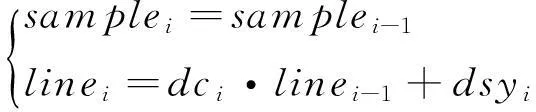
(5)

式中：dci为第i景影像相对于第(i-1)景影像的沿归向缩放系数；dsyi是第i景影像相对于第(i-1)景影像的平移系数。当以第1景影像为基准，恢复整轨的条带影像时，则可以得到如下关系式，即

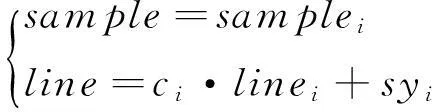
(6)

式中：ci为第i景影像与条带影像间的缩放参数；syi为第i景影像与条带影像之间的平移参数。其中

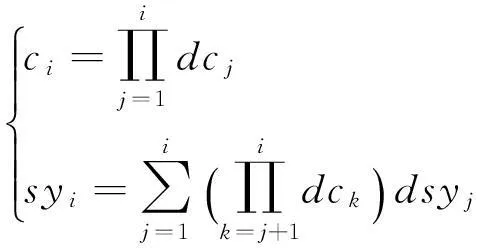
(7)

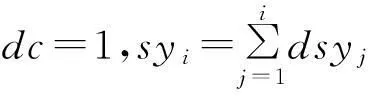
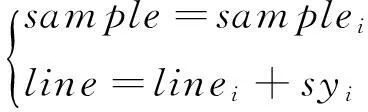
(8)

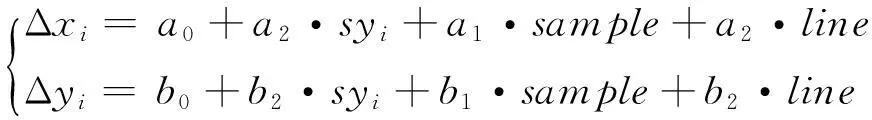
(9)

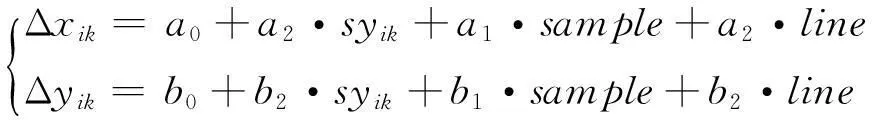
(10)

式中：syik为第k段的平移参数；sy1k为第k段第1景影像的平移系数。针对式(10)建立误差方程，即

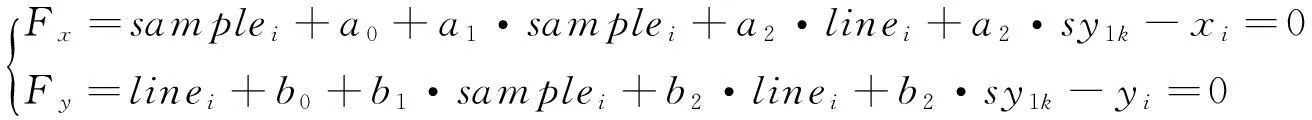
(11)

对于第k段条带影像上的控制点来说，未知数为平差参数(a0,a1,a2,b0,b1,b2,sy1k)； 而对于连接点来说，未知数包括平差参数和相应的物方坐标(lat,lon,h)。因此，对于1轨n段影像来说，所需求解模型精化参数个数为(n+5)个，而控制点数目不应少于(n+2)个。

对式(11)进行一阶泰勒级数展开，可得到线性化的误差方程，即

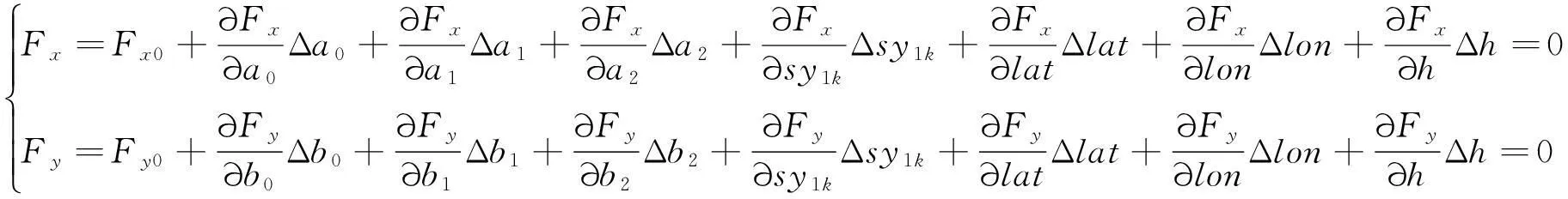
(12)

将式(1)(2)(11)带入式(12)，可得到间接平差模型，即

V=AX+BY-L，P ，

(13)

式中： X=[Δa0Δa1Δa2Δb0Δb1Δb2sy1k],

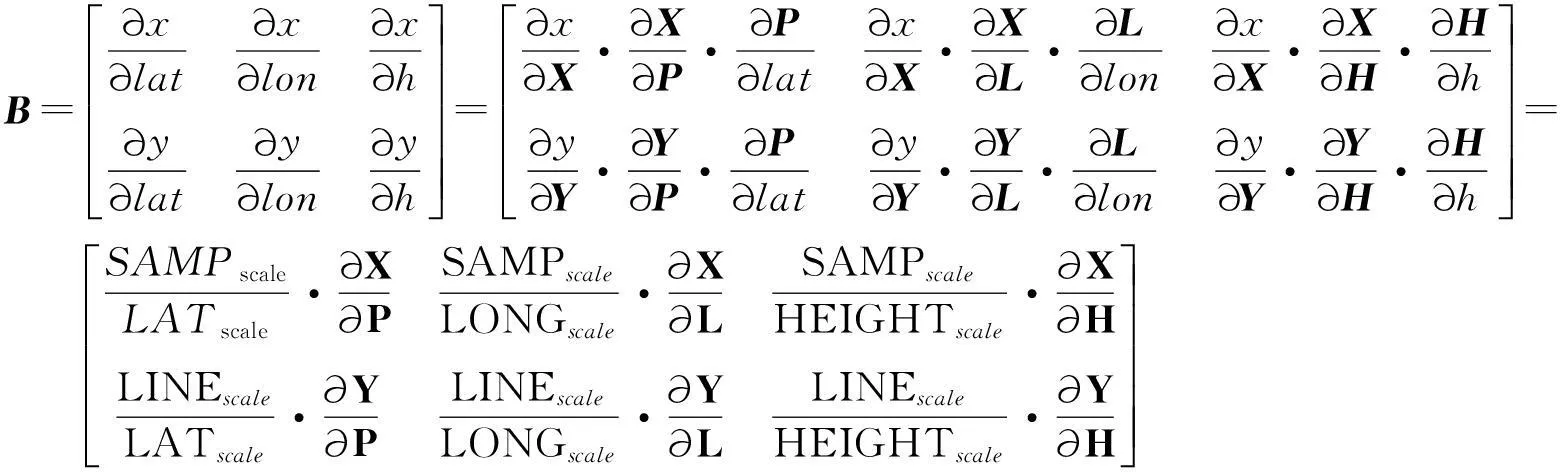
(14)

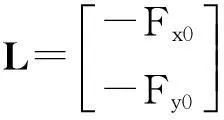
对于控制点来说，B=0。当同时存在控制点和连接点时，即可建立如下误差方程，即

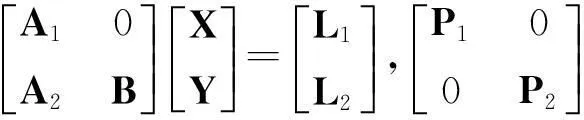
(15)

对于2类未知数的误差方程，可以消除第2类未知数Y，得到相应的改化法方程，即

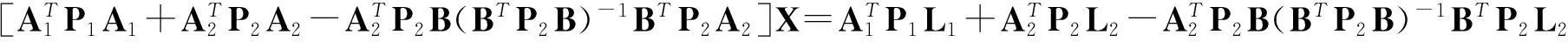
(16)

当连接点的交会角满足一定条件时，矩阵BTP2B的逆存在； 当缺少足够的控制点时，式(16)的系数矩阵秩亏。可以通过岭估计或者截断奇异值分解等方法进行正则化求解。

3实验结果与分析

3.1实验数据

本文采用覆盖张家口地区的ZY-3测绘卫星同轨7景标准景的三线阵影像和覆盖北京怀柔地区的IRS-P5卫星两轨4景影像作为实验数据。ZY-3影像的时相为2012年1月29日，影像的起始部分有少量雪覆盖，最后1景影像中有少许云覆盖。在实验区范围内均匀布设大量地面控制点，均匀分布在影像范围内，间隔约10km。选取的控制点大部分为道路交叉口，少量为地物拐角处； 在控制点选取比较困难的山区，部分道路的锐角相交处被选作了控制点。因测区范围较大，控制点均利用TOPCONNET-G3A单点静态观测，经地面数据处理后，定位精度在10cm之内。经过剔除部分无法识别的点位以及小角度道路交汇处之后，余下的193个控制点在平面和高程上均匀分布(图1)。

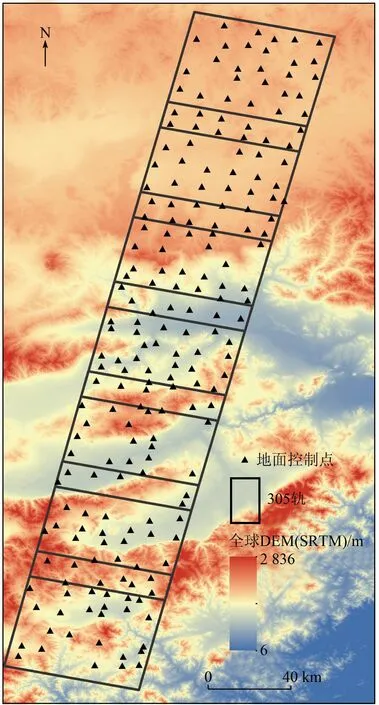
图1　ZY-3后视影像及控制点分布示意图

IRS-P5为两线阵卫星，由前后视相机获取立体影像； 其中，前视相机下视角为26°，后视相机下视角为5°。IRS-P5卫星影像数据由2个相邻轨道组成，每个轨道的影像包含2个标准景，分别覆盖北京怀柔和密云地区。该地区共有33个控制点，控制点在影像中均匀分布(图2)。控制点通过差分GPS测得，测量精度为10cm。

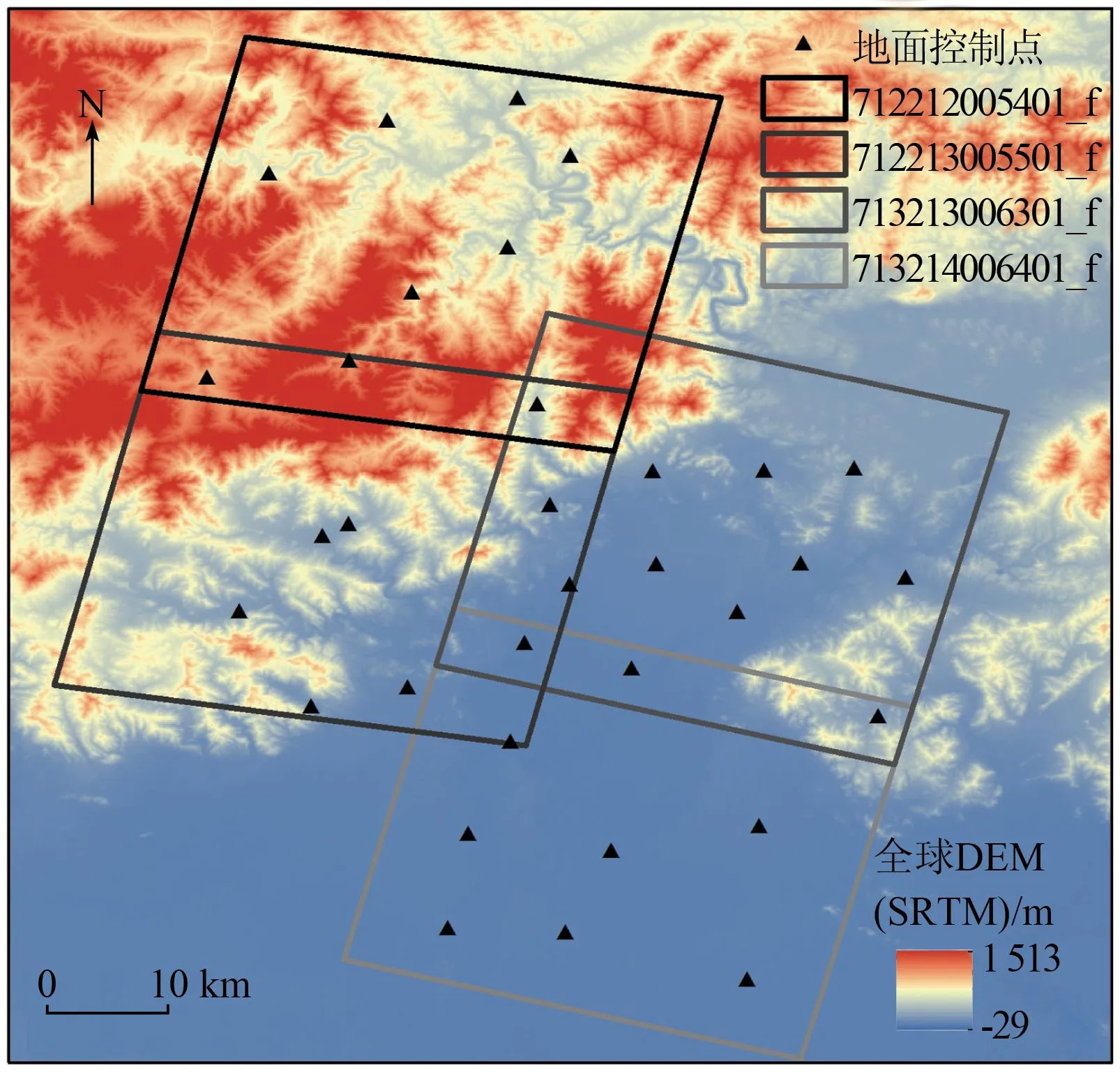
图2　IRS-P5 前视影像及控制点分布示意图

3.2ZY-3测绘卫星影像平差实验

针对ZY-3测绘卫星数据，本文采用了3种不同平差策略进行验证： ①基于条带影像产品的区域网平差； ②基于同轨约束的标准景影像区域网平差； ③基于标准景影像的区域网平差。而控制点分别采用无控制点、4角点布设控制点和条带均匀布设16个控制点3种不同的控制点布设方案，其平差精度见表1。

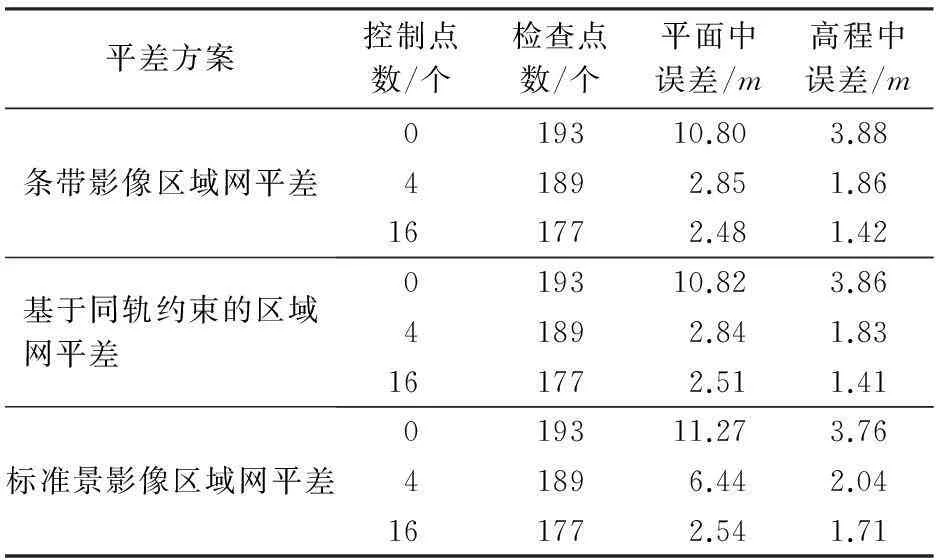
表1　ZY-3影像各平差结果对比

从表1可以看出，3种不同实验方案的无控制点立体平差精度差异较小，平面中误差约为11m，高程中误差约为4m。

当采用4角点布设控制点时，条带影像的区域网平差精度平面中误差为2.85m，高程中误差为1.86m； 基于同轨约束的标准景影像平差的平面中误差为2.84m，高程中误差为1.83m； 而标准景影像区域网平差由于缺少足够的控制点，其系数矩阵严重病态，平面中误差达6.44m，高程中误差达2.04m。条带影像产品与基于同轨约束的标准景影像的误差几乎相同。

当控制点数目增加到16个时，使得标准景影像上均有4个控制点覆盖，条带影像的平面中误差为2.48m，高程中误差为1.42m，精度进一步得到提升； 而基于同轨约束的标准景影像的平面中误差为2.51m，高程中误差为1.41m，两者几乎没有差异； 标准景影像平面中误差为2.54m，高程中误差为1.71m，比同轨约束和条带影像产品的高程精度略差，与标准景所能达到的精度相近[15]。

通过比较基于同轨约束的区域网平差的残差图(图3(a))与无约束的区域网平差的残差图(图3(b))可以看出，其残差的方向相同； 而基于同轨约束的区域网平差的高程残差要小于未加入同轨约束的高程残差。由于为每景影像单独求解相应的平差参数，因此受单个控制点的影响较大。当1景影像内出现质量较差的控制点时，整景影像的残差将会变大(如第3景影像中的高程方向)。

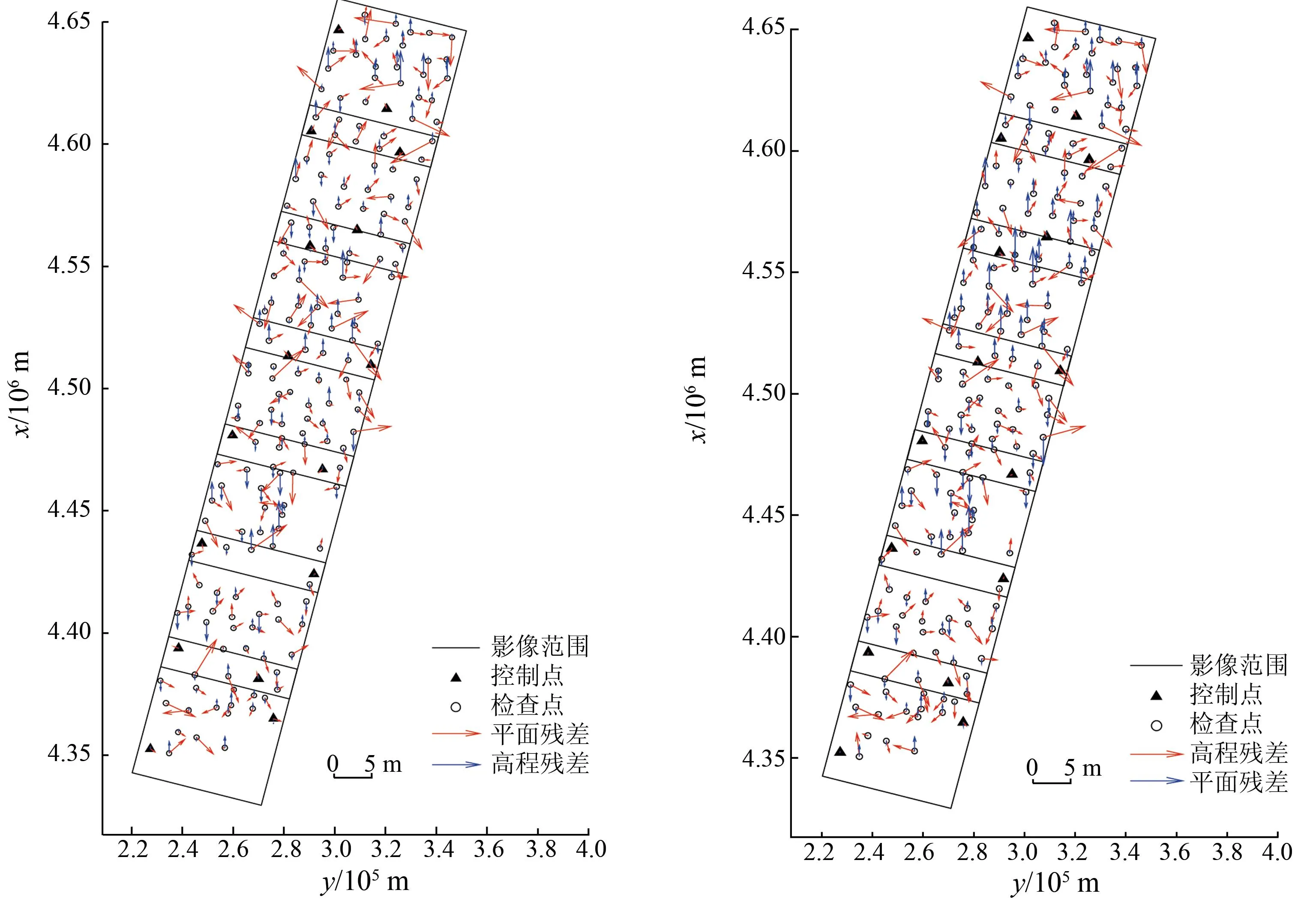
(a) 基于同轨约束的区域网平差 (b) 无约束的区域网平差

图3305轨道标准景影像16个控制点平差误差分布

Fig.3Residualerrorsoforbit305standardscenesbyusingbundleadjustmentof16GCPs

3.3IRS-P5影像平差实验

因无法获取IRS-P5卫星的条带影像产品，故只能对其标准景影像平差和基于同轨约束的区域网平差进行对比分析。对于上述2种平差实验，采用4种控制点布设方案： ①无控区域网平差； ②5个控制点的区域网平差，保证每个轨道中有3个控制点； ③8个控制点的区域网平差，保证每景影像中有3个控制点； ④10个控制点的区域网平差，保证每景影像中有4个控制点。实验结果见表2。

当所有的控制点作为检查点参与区域网平差时，标准景影像区域网平差和基于同轨约束的区域网平差的精度相近，平面中误差均为290m左右，高程中误差为110m左右。而当仅只有5个控制点时，基于同轨约束的区域网平差的平面中误差为3.26m，高程中误差为2.38m； 对于标准景区域网平差，其未知数的个数多于观测值个数，因此其平差精度要远低于基于同轨约束的区域网平差，此时平面中误差为28.08m，高程中误差为14.89m。当控制点数目为8个时，基于标准景的区域网平差有足够的观测值，因此其平面中误差为3.09m，高程中误差为2.52m； 基于同轨约束的区域网平差的平面中误差为2.67m，高程中误差为2.13m。当控制点数目进一步增加到10个时，基于同轨约束的区域网平差平面中误差为2.55m，高程中误差为1.98m； 而标准景影像区域网平差的平面中误差为2.89m，高程中误差为2.15m。

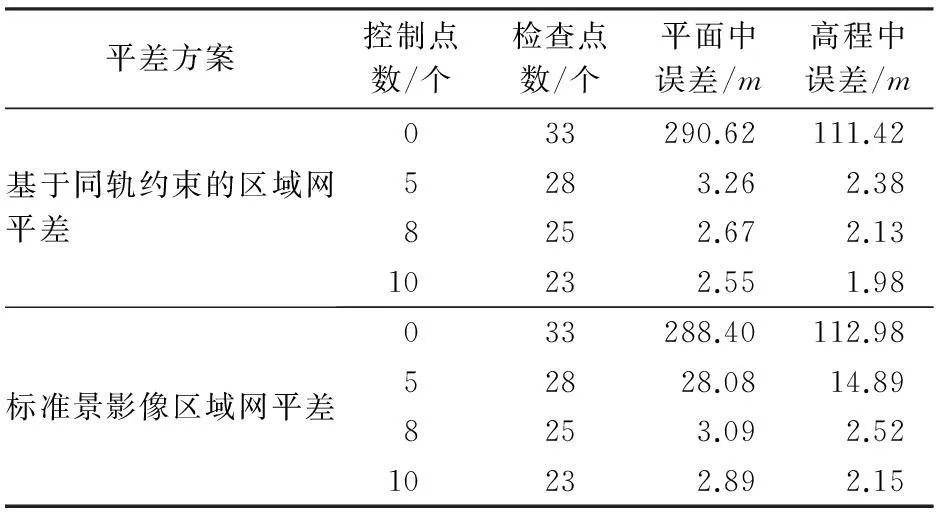
表2　IRS-P5影像各平差结果对比

实验结果表明，基于同轨约束的区域网平差仅需要较少的控制点即可实现对整个条带影像的定向； 而在控制点数目相同时，基于同轨约束的区域网平差由于其包含更多的多余观测，因此其平差结果较标准景影像的区域网平差更为稳定，受控制点误差影响更小，平差精度更高。

4结论

本文通过将标准景影像生产过程与条带影像产品生产过程对比，建立了同轨相邻景标准景影像之间的几何关系。将上述几何关系应用于基于RFM的区域网平差中，得到了基于同轨约束的区域网平差方案。得出如下结论：

1)由于同轨影像之间的几何约束，大幅度减少了对控制点数目的要求，使得利用少量控制点即可达到大量控制点的精度水平。

2)通过用我国ZY-3测绘卫星和印度IRS-P5卫星影像进行区域网平差的实验表明： ①基于同轨约束的区域网平差需要的控制点更少； ②在相同数目控制点的情况下，基于同轨约束的区域网平差精度较标准景区域网平差精度高； ③基于同轨约束的区域网平差能达到与长条带影像产品相当的精度。

3)受数据条件限制，本文仅对ZY-3和IRS-P5的高分影像数据开展了有限的实验，在今后的工作中将进一步探讨轨道长度与平差模型的关系，并将本文的方法进一步应用于其他的高分卫星(如WorldView,Pleiades等)。

参考文献(References)：

[1]张力,张继贤,陈向阳,等.基于有理多项式模型RFM的稀少控制SPOT-5卫星影像区域网平差[J].测绘学报,2009,38(4):302-310.

ZhangL,ZhangJX,ChenXY,etal.Block-adjustmentwithSPOT-5imageryandsparseGCPsbasedonRFM[J].ActaGeodaeticaetCartographicaSinica,2009,38(4):302-310.

[2]王任享.三线阵CCD影像卫星摄影测量原理[M].北京:测绘出版社,2006.

WangRX.SatellitePhotogrammetricPrincipleforThree-Line-ArrayCCDImagery[M].Beijing:SurveyingandMappingPress,2006.

[3]KimT,KimH,RheeS.InvestigationofphysicalsensormodelsformodellingSPOT3orbits[J].ThePhotogrammetricRecord,2007,22(119):257-273.

[4]GuptaA,NainJS,SinghSK,etal.LongstripmodellingforCARTOSAT-1withminimumcontrol[C]//InternationalArchivesofthePhotogrammetry,RemoteSensingandSpatialInformationSciences.Beijing,China,2008:717-722.

[5]程春泉,邓喀中,孙钰珊,等.长条带卫星线阵影像区域网平差研究[J].测绘学报,2010,39(2):162-168.

ChengCQ,DengKZ,SunYS,etal.Studyofblockadjustmentforlong-stripsatelliteCCDimages[J].ActaGeodaeticaetCartographicaSinica,2010,39(2):162-168.

[6]RottensteinerF,WeserT,LewisA,etal.AstripadjustmentapproachforprecisegeoreferencingofALOSopticalimagery[J].IEEETransactionsonGeoscienceandRemoteSensing,2009,47(12):4083-4091.

[7]GrodeckiJ,DialG.Blockadjustmentofhigh-resolutionsatelliteimagesdescribedbyrationalpolynomials[J].PhotogrammetricEngineering&RemoteSensing,2003,69(1):59-68.

[8]DiK,MaR,LiR.Rationalfunctionsandpotentialforrigoroussensormodelrecovery[J].PhotogrammetricEngineering&RemoteSensing,2003,69(1):33-41.

[9]FraserCS,HanleyHB.Bias-compensatedRPCsforsensororientationofhigh-resolutionsatelliteimagery[J].PhotogrammetricEngineering&RemoteSensing,2005,71(8):909-915.

[10]张过,潘红播,唐新明,等.资源三号测绘卫星长条带产品区域网平差[J].武汉大学学报:信息科学版,2014,39(9):1098-1102.

ZhangG,PanHB,TangXM,etal.BlockadjustmentofZY-3longstripscenes[J].GeomaticsandInformationScienceofWuhanUniversity,2014,39(9):1098-1102.

[11]张过,汪韬阳,李德仁,等.轨道约束的资源三号标准景影像区域网平差[J].测绘学报,2014,43(11):1158-1164,1173.

ZhangG,WangTY,LiDR,etal.BlockadjustmentforZY-3satellitestandardimagerybasedonstripconstraint[J].ActaGeodaeticaetCartographicaSinica,2014,43(11):1158-1164,1173.

[12]ZhengMT,ZhangYJ,ZhuJF,etal.Self-calibrationadjustmentofCBERS-02Blong-stripimagery[J].IEEETransactionsonGeoscienceandRemoteSensing,2015,53(7):3847-3854.

[13]潘红播,张过,唐新明,等.资源三号测绘卫星传感器校正产品几何模型[J].测绘学报,2013,42(4):516-522.

PanHB,ZhangG,TangXM,etal.ThegeometricalmodelofsensorcorrectedproductsforZY-3satellite[J].ActaGeodaeticaetCartographicaSinica,2013,42(4):516-522.

[14]王家骐,于平,颜昌翔,等.航天光学遥感器像移速度矢计算数学模型[J].光学学报,2004,24(12):1585-1589.

WangJQ,YuP,YanCX,etal.Spaceopticalremotesensorimagemotionvelocityvectorcomputationalmodeling[J].ActaOpticaSinica,2004,24(12):1585-1589.

[15]潘红播,张过,唐新明,等.资源三号测绘卫星影像产品精度分析与验证[J].测绘学报,2013,42(5):738-744,751.

PanHB,ZhangG,TangXM,etal.AccuracyanalysisandverificationofZY-3products[J].ActaGeodaeticaetCartographicaSinica,2013,42(5):738-744,751.

(责任编辑： 刘心季)

Block adjustment of high resolution satellite image usingRFMwiththesamestripeconstraint

PAN Hongbo1， ZOU Zhengrong1， ZHANG Guo2， ZHANG Yunsheng1， WANG Taoyang3

(1. School of Geosciences and Info-Physics， Central South University， Changsha 410083， China； 2. State Key Laboratory of Information Engineering in Surveying， Mapping and Remote Sensing， Wuhan University， Wuhan 430079， China；3. School of Remote Sensing and Information Engineering， Wuhan University， Wuhan 430079， China)

Abstract:Generally,standardsceneswithrationalfunctionmodel(RFM)areprovidedtousersasthecommonformofhighresolutionsatelliteimages.SinceRFMparameterslackclearphysicalsignificance,thegeometricconstraintrelationshipofstandardscenesinthesamestripecouldhardlybeestablishedeventhoughbothattitudeandephemeriserrorsarestableinthesamestripe.Onthebasisofthedifferencebetweenstripescenesandstandardscenes,aswellasinconsiderationoftheoffseteffectandintegraltimedifferencesofstandardscenes,astripeconstraintmethodbasedontheimage-spacepolynomialmodelisproposedinthispaper,whichcouldbeusedtoconstrainthediscontinuousstandardscenesinthesamestripeandrealizethestripe-constrainedblockadjustmentofhigh-resolutionimages.TripletstereoscoveringsevenstandardscenesofZY-3andtwoadjacentstripesofIRS-P5wereusedfortheexperiment.Theresultsshowthat,withtheproposedmethodinthispaper,lessgroundcontrolpointsarerequiredforblockadjustmentwiththesamestripeconstraint,andthehigheraccuracyispromisedaswell.

Keywords:highresolutionsatelliteimage；samestripconstraint；blockadjustment；rationalfunctionmodel(RFM)

doi:10.6046/gtzyyg.2016.03.08

收稿日期：2015-03-26；

修订日期：2015-05-05

基金项目：中国博士后科学基金面上项目“高分辨率光学卫星姿态模型研究”(编号： 2015M572268)和中国测绘科学研究院基本科研业务费项目共同资助。

中图法分类号：TP 751.1

文献标志码：A

文章编号：1001-070X(2016)03-0046-07

第一作者简介：潘红播(1987-),男,博士,讲师,主要从事航天摄影测量方面研究。Email：hongbopan@csu.edu.cn。

引用格式： 潘红播,邹峥嵘,张过,等.基于同轨约束RFM的高分卫星影像区域网平差[J].国土资源遥感,2016,28(3)：46-52.(Pan H B,Zou Z R,Zhang G,et al.Block adjustment of high resolution satellite image using RFM with the same stripe constraint[J].Remote Sensing for Land and Resources,2016,28(3)：46-52.)