洪水位变化对堤防稳定的影响

2016-07-16范瑞朋

水利水电工程设计 2016年1期

关键词：稳定渗流洪水位非饱和

朱　涛　訾　娟　范瑞朋　任　堂

洪水位变化对堤防稳定的影响

朱涛訾娟范瑞朋任堂

摘要介绍了堤防在洪水过程中边坡稳定的影响因素，并根据geo-studio软件计算了一个堤防边坡在水位下降过程中的非饱和非稳定渗流和稳定渗流，得到了堤防边坡渗流变化规律和安全系数，并采取了提高堤防稳定的措施。

关键词堤防稳定洪水非饱和非稳定渗流

随着我国经济建设的快速发展和河道整治的逐步完善，堤防的安全问题也越来越多地呈现在人们面前。堤防的破坏因素除了常见的冲刷、流土、管涌之外，一个重要的破坏因素就是洪水消退引起的渗透破坏。一般情况下，洪水历时短，强度大，不如水库水位容易控制，所以堤防的水位在短时间内有暴涨暴落的情况，极大地影响了堤防迎水面边坡的稳定性。

1　堤防边坡稳定分析原理

1.1边坡渗流原理

洪水位变化是堤防边坡稳定的重要影响因素。河道堤防多为均质土堤，渗透系数较小，渗流浸润线的变化总滞后于洪水位的变化［1］。

洪水位骤降时，堤内水来不及排出，浸润线最高处高于洪水位，不仅使边坡体迎水面形成较大的水力梯度和流向河道的不稳定渗流，而且由于土体内孔隙水压力不能很快消散［2］，形成超孔隙水压力，减小土粒之间的有效应力［3］，影响堤防边坡稳定。由于河道水位下降过程中，下游边坡水位总是下降的，对下游坡影响较小，故本次分析只分析水位骤降对堤防迎水面边坡稳定的影响［4］。

1.2非饱和与非稳定渗流的数学模型

非饱和与非稳定渗流的基本方程：

式中θw——体积含水率；

kwij——渗透系数；

Pw，j——Pw在j方向上的导数；

bj——单位体积力；

ρ——水的密度；

g——重力加速度。

土的饱和度和基质吸力的关系公式：

式中n——孔隙率。

总水头φw的计算公式：

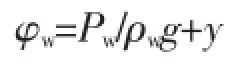
式中y——位置水压。

假定y轴与重力加速度方向相反，即可得以总水头φw为变量的基本方程：根据此方程采用非线性迭代计算，即可求解得每个时间点的孔压分布值和浸润线的位置［2］。

1.3非饱和土抗剪强度理论

饱和土的抗剪强度指标一般利用摩尔库伦破坏准则进行判断，但是对于非饱和土，由于气体的存在，其强度理论十分复杂，经典的饱和土力学不能精确表达。国内外有很多研究，其中Fredlund的双参数模型应用较广。

1.4计算软件原理

本次计算采用的软件是 Geo-studio软件的SEEP/W和Slope/W模块。

SEEP/W计算模块采用的是基于饱和、非饱和土体渗流的达西定律［5］，通过建立渗流模型，进行有限元计算，可以分析堤防边坡在饱和条件、非饱和水条件下的渗流随时间的变化。Slope/W计算模块采用的是Morgenstern-Price（摩根斯坦-普林斯）法：对任意曲线形状的滑裂面进行了分析，导出满足力的平衡和力矩平衡条件的微分方程组，然后假定两相邻土条在法向条间力和切向条间力之间存在对水平方向坐标的函数关系，最后根据整个滑动土体的边界条件求出问题的解答［6］。

2　工程实例及分析

本次计算根据天津大清河的一段堤防的参数和相应的典型洪水过程计算堤防在洪水过程中的稳定性。

2.1工程概况

堤防建筑物级别为二级，堤高7.4 m，堤顶宽度4.0 m，上游边坡1∶2.0，下游边坡1∶2.0，河道正常水位1.8 m，设计洪水位5.1 m。见图1。

图1　均质土堤体型图（单位：m）

2.2计算参数

边坡为均质黏土边坡，黏土填筑容重19.0 kN/ m3，黏聚力15 kPa，内摩擦角18°，孔隙率为0.4，饱和含水度0.4 m3/m3，残余含水度为0.16 m3/m3，渗透系数为1×10-6m/s。

假设河道水位是均匀下降的，模拟设计洪水在一定时间段内由设计洪水位下降到正常水位的渗流过程。

2.3计算结果

2.3.1水位骤降对渗流的影响

河道水位下降速度较快，但是堤防的渗透系数较小，造成堤防内上游侧饱和土壤中的水并没有随之迅速排出，造成渗流变化滞后于河道水位变化，在坡内维持较高的浸润线。随着时间的延长，堤防内的浸润线逐渐降落，最终与河道水位持平。在浸润线降落的这段时间内，堤防上游坡形成流向上游的渗流。河道水位在水位变化周期T=24 h和T=48 h内从设计洪水位匀速至正常水位时，浸润线随时间变化情况见图2（虚线为T=24 h的浸润线情况，实线为T=48 h的浸润线情况）。

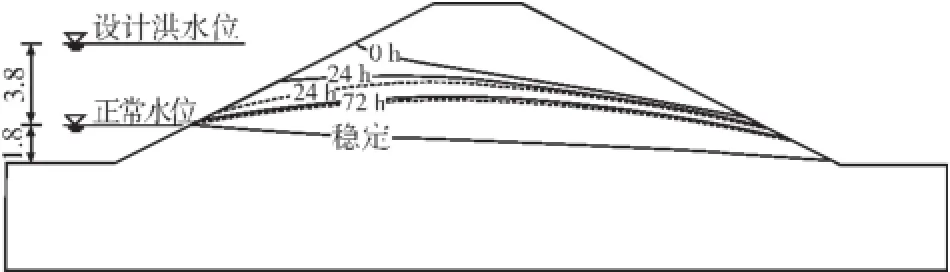
图2　浸润线变化对比曲线图（长度单位：m）

从图2可以看出，浸润线变化明显滞后于河道水位变化，呈现上凸的形状，T=24 h的浸润线变化幅度大于T=48 h。随着渗径的延长，中下游侧浸润线变化并不明显。

2.3.2水位骤降对稳定的影响

在河道水位下降的过程中，超孔隙水压力和流向河道的逆向渗流对堤防上游侧的稳定不利。河道水位降落过程中的上游坡安全系数详见表1。从表中可以看出，随着河道水位的下降，上游侧边坡的安全系数逐渐减小，至上游侧水位降至正常水位时安全系数最小，然后随着浸润线的降低，安全系数逐渐加大直至稳定边坡的安全系数。

表1　迎水面边坡安全系数

图3给出了在设计洪水位（h=5.1 m）、正常水位（h=1.8 m）稳定渗流工况和河道水位骤降至正常水位（T=48 h和T=24h）工况下的堤防上游侧边坡安全系数和滑弧。从图可以看出，在设计洪水位和正常蓄水位稳定渗流工况下，上游堤坡安全系数为2.272和1.701；T=48 h工况下，安全系数最小为1.565；T=24 h工况下，安全系数最小为1.331，安全系数均大于规范规定的最小值1.20，堤坡安全。考虑到堤坡较长，试验资料代表性有限，而且存在施工质量不均一的情况，故堤前水位由设计水位骤降至正常蓄水位的时间应控制在不小于48 h。

图3　4个工况下堤防上游侧滑弧和安全系数图

2.4处理措施

2.4.1下游加排水棱体

堤防不同于均质土坝，水头较低，堤体较薄，采取人工措施对浸润线的控制较容易。本次计算的堤内浸润线较平缓，而且下游溢出点较高，如果下游设置排水，可有效降低浸润线，不仅对下游边坡有利，而且对上游边坡也会产生一定的有利影响。

本文考虑下游设置1.5 m长的排水褥垫。比较在T=48 h水位骤降工况下，设置排水褥垫的浸润线与不设置排水褥垫的浸润线变化情况。设置褥垫排水后，堤内浸润线整体下降，尤其在中下游侧下降明显，安全系数比较详见表1。从表中可以看出，下游增加棱体排水后，上游侧边坡的安全系数有较小的增加，但影响不大。

2.4.2采用渗透系数较高的填筑料

渗透系数k=1×10-5m/s，其他参数不变的情况下，设计洪水在T=24 h和T=48 h时间内由设计洪水位下降到正常水位的过程中，堤防的浸润线变化情况和同等水头下稳定渗流的浸润线比较见图4和图5（其中：实线为水位骤降工况，虚线为稳定渗流工况）。从图可以看出，水位骤降工况下浸润线变化略滞后于稳定渗流浸润线，但是没有呈现明显上凸的形状，浸润线整体较平稳。说明堤防在渗透系数k=1×10-5m/s的情况下，土壤的渗透能力加大，在河道水位下降时，上游浸润线也能较快下降，对边坡稳定的影响不大。