自适应GM(1,1)模型在码头位移变形预测中的应用*1
2016-07-16张巧英
张巧英
(浙江省测绘大队,浙江 杭州 310030)
自适应GM(1,1)模型在码头位移变形预测中的应用*1
张巧英
(浙江省测绘大队,浙江 杭州310030)
摘要:码头水工建筑物,由于其工作环境的特殊性,通常会发生位移变形,通过对码头的位移变形预测分析,能够更好地掌握码头的变形规律并及时预警,确保码头的安全运营。针对传统GM(1,1)模型仅适用于短期且呈指数变化趋势的变形预测分析的局限性,建立自适应GM(1,1)模型,并将该模型引入到实际工程应用中,依据某码头的位移监测数据进行变形预测分析。结果表明:自适应GM(1,1)模型预测精度高于传统GM(1,1)模型,自适应GM(1,1)模型具有更好的预测效果和应用价值。
关键词:传统GM(1,1)模型;自适应GM(1,1)模型;码头;变形预测
0引言
随着水运事业的发展,码头的数量及其装卸吨位都在快速的增加。码头水工建筑物的复杂性及其工作环境的特殊性,且其向海测方向的位移,对码头的安全运营造成不利的影响。因此,对码头位移现象进行变形监测分析,通过正确可靠的监测数据及时发现问题、采取有效措施解决问题,减少变形对码头功能的影响,并总结变形规律,这是确保码头安全运营的迫切要求。
目前,变形分析与预测的方法主要有回归分析法、时间序列法、人工神经网络法等。以上各种建模方法在具有较长的数据序列时,都可获得较理想的预测结果,但是对于信息量小且规律性较弱的短数据序列,则限制了某些方法的应用范围,使其达不到理想预测结果;传统GM(1,1)模型针对这种问题具有一定的优势,但是传统GM(1,1)模型只是从静态方面考虑未来的状态,并没有加入未来可能影响到系统状态的因素,所以在实际工程应用中有时也难以达到精度要求[1]。因此,本文针对这一情况,依据某码头的位移监测数据,基于Matlab 软件平台,建立自适应GM(1,1)模型,并通过实测数据与预测数据的对比分析,得出自适应GM(1,1)模型的预测精度高于传统GM(1,1)模型的结论。
1传统GM(1,1)模型
传统GM(1,1)模型的建模过程[2-4]为:
令x(0)为非负原始数据序列:
x(0)=(x(0)(1),x(0)(2),…,x(0)(n))
(1)
对x(0)进行一次累加生成,记x(1)=1-AGOx(0),则:
x(1)=(x(1)(1),x(1)(2),…,x(1)(n))
(2)
(3)
式中:a,b为待定常数,其中a为发展系数(即控制系统发展态势的大小),b为灰色作用量(即反映数据的变化关系)。式(3)为GM(1,1)的白化方程。
GM(1,1)白化方程的时间响应式(即白化方程的解):
(4)
通过累减生成GM(1,1)模型:
(5)
2自适应GM(1,1)模型
传统GM(1,1)模型建模数据是t=n为止的旧数据,是一种静态模型,随着时间的推移,未来数据的一些随机噪声及扰动因素会进入系统,含有较多的干扰成分,影响模型的后期预测效果及精度[5]。为确保动态变形分析的可靠性,需要顾及未来数据的一些随机噪声和扰动因素的影响,在建立GM(1,1)模型时,引入新数据构成新数据序列,根据新数据序列建立新的GM(1,1)模型[5]。
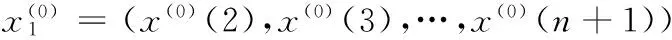
3模型精度检验
实测数据列方差:
(6)
残差方差:
(7)
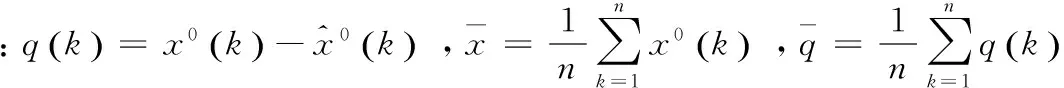
后验差比值:
(8)
小误差概率:
(9)
模型精度按照C和P两个指标进行综合判定,如表1[7-8]所示。
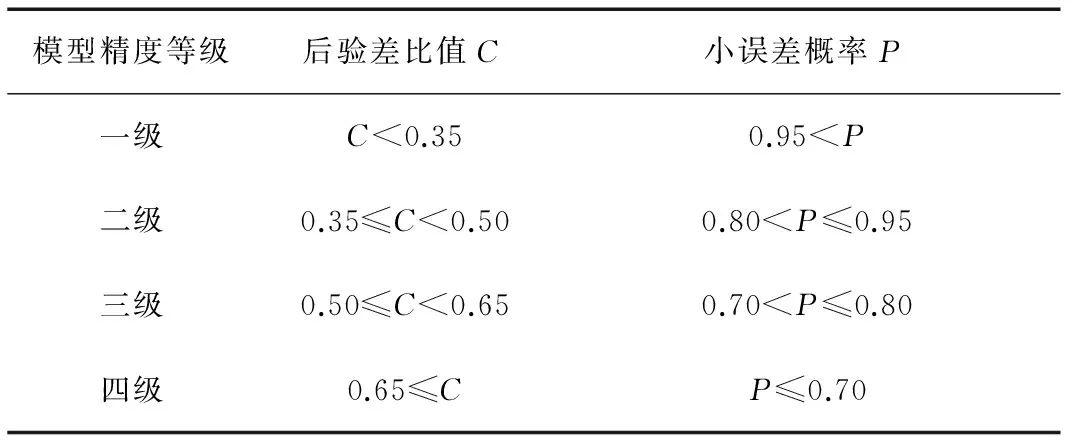
表1 后验差检验法精度等级表
4应用实例
使用Leica TM30全站仪对某码头进行水平位移监测,监测周期为60 d。该码头共布设58个监测点,通过对码头的多个监测点的位移监测数据(X、Y分别表示监测点不同时期的X坐标、Y坐标)进行变形分析,总结得知所分析监测点变形规律具有一定的相似性。现以某监测点连续12期的监测数据为例,利用预测模型对前8期监测数据进行建模,预测后4期数据,并根据实测数据与预测结果进行对比分析,如表2、表3所示。

表2 实测值与预测值对比

表3 两种模型的精度对比
由表2可知:从模型的拟合残差分析,自适应GM(1,1)模型对监测点不同时期X坐标和Y坐标的拟合残差绝对值除第3期大于传统GM(1,1)模型外,其他7期的拟合残差绝对值均小于传统GM(1,1)模型,拟合效果较好;从模型的预测残差分析,自适应GM(1,1)模型对监测点不同时期X坐标和Y坐标的预测残差绝对值均小于GM(1,1)模型,预测值较接近实测值,预测效果较好。
由表3可知:从后验差比值分析,自适应GM(1,1)模型对不同时期X坐标、Y坐标预测后验差比值分别为0.291 8、0.349 9,均小于传统GM(1,1)后验差比值0.522 5、0.569 6;从小误差概率分析,自适应GM(1,1)模型对不同时期X坐标、Y坐标预测小误差概率分别为1.000 0、0.916 7,均大于传统GM(1,1)小误差概率0.833 3、0.833 3;从模型精度等级分析,自适应GM(1,1)模型对不同时期X坐标和Y坐标的预测精度等级分别由三级提升至一级和二级,使预测精度有所改善。X、Y方向模型预测对比图,分别见图1、图2。
由图1、图2可知:从X方向位移变形分析,自适应GM(1,1)模型预测X方向位移变形曲线较传统GM(1,1)模型接近实测位移变形曲线,自适应GM(1,1)模型预测残差值也相对较小,在0附近波动,波动较小,相对较稳定;同理,从Y方向位移变形分析,自适应GM(1,1)模型预测结果也能更好地反映实测位移变形趋势,相比于传统GM(1,1)模型,自适应GM(1,1)模型具有较高预测精度。因此,自适应GM(1,1)模型相对传统GM(1,1)模型具有更好的预测效果。

图1 X方向模型预测对比图Fig.1 Comparison of models’ prediction values in X direction

图2 Y方向模型预测对比图Fig.2 Comparison of models’ prediction values in Y direction
5结束语
针对传统GM(1,1)模型仅适用于短期且呈指数变化趋势的变形分析与预测的局限性,建立自适应GM(1,1)模型,并引入到工程实例中,以某码头监测数据为例进行验证分析,结果表明:
自适应GM(1,1)模型是一种动态建模方法,通过实时剔除旧数据,不断注入新数据,确保建模数据序列的及时更新,建立递补动态模型;自适应GM(1,1)模型不仅能够更好地反映最新的变形趋势,而且可以消弱未来数据扰动因素随时间推移对模型预测精度的影响,消除预测模型的噪声污染,改善传统GM(1,1)静态模型的不足,有效地提高模型的预测精度,具有更好的应用价值。
[参考文献]
[1]王利,张双成,李亚红.动态灰色预测模型在大坝变形监测及预报中的应用研究[J].西安科技大学学报,2005,25(3):328-332.
[2]邓聚龙.灰色系统基本方法[M].1版.武汉:华中科技大学出版社,2005.
[3]秦晓光,杨龙才.灰色预测在高铁路基沉降预测中的应用[J].华东交通大学学报,2011,28(5):88-92.
[4]张正禄,黄全义,文鸿雁,等.工程的变形监测分析与预报[M].北京:测绘出版社,2007:146-155.
[5]周吕,文鸿雁,胡纪元,等.改进GM(1,1)在高铁隧道沉降变形预测中的对比应用[J].施工技术,2014,43(18):66-68,81.
[6]潘华志,卫建东,夏治国,等.动态灰色模型在变形预测中的应用[J].测绘科学,2007,32(4):121-123.
[7]张建雄,蒋金豹,张建霞.高层建筑沉降监测与灰色预测[J].测绘科学,2007,32(4):56-59.
[8]何君,杨国东.灰色预测理论在建筑物沉降中的应用研究[J].测绘通报,2012(3):63-64.
Application of Self-Adaptive GM(1,1)Model in Displacement Deformation Prediction of Wharf
ZHANG Qiao-ying
(ZhejiangBrigadeofSurveyingandMapping,HangzhouZhejiang310030,China)
Abstract:Wharf hydraulic structures,due to its particularity of the working environment,the displacement deformation usually occurs there.By predicting and analyzing the displacement deformation of wharf,it can be better to grasp the deformation regularity of the wharf and warn timely,which ensures the safe operation of wharf.According to the fact that traditional GM(1,1)model only suits for short-term and exponential variation trend deformation analysis and prediction,an self-adaptive GM(1,1)model was built in this paper and applied it to the practical engineering.The deformation analysis results can be obtained by processing the displacement monitoring data of a wharf.The result shows that the self-adaptive GM(1,1)model has a higher prediction accuracy than the traditional GM(1,1)model.Therefore,self-adaptive GM(1,1)model has a better forecast effect and application value.
Key words:traditional GM(1,1)model;self-adaptive GM(1,1)model;wharf;deformation prediction
* 收稿日期:2016-03-16
中图分类号:P 258
文献标识码:B
文章编号:1007-9394(2016)02-0042-03
作者简介:张巧英(1976~),女,浙江嵊州人,高级工程师,现主要从事地理信息系统应用研究方面的工作。
地矿测绘2016,32(2):42~44
CN 53-1124/TDISSN 1007-9394
Surveying and Mapping of Geology and Mineral Resources
