单晶γ-TiAl中孔洞位置对裂纹扩展影响的分子动力学模拟*
2016-07-16罗德春芮执元陈文科剡昌锋
罗德春,芮执元,曹 卉,陈文科,剡昌锋
(1. 兰州理工大学 机电工程学院, 兰州 730050;2. 兰州理工大学 数字制造技术与应用省部共建教育部重点实验室, 兰州 730050)
单晶γ-TiAl中孔洞位置对裂纹扩展影响的分子动力学模拟*
罗德春1,2,芮执元1,2,曹卉1,2,陈文科1,剡昌锋1,2
(1. 兰州理工大学 机电工程学院, 兰州 730050;2. 兰州理工大学 数字制造技术与应用省部共建教育部重点实验室, 兰州 730050)
摘要:运用分子动力学方法对单晶γ-TiAl合金的裂纹扩展过程进行了研究,分析了不同孔洞位置对裂纹扩展的影响,得到相应的原子轨迹、能量演化以及应力-应变关系。结果表明无孔洞时,裂纹以脆性解理方式快速扩展至材料断裂,能量曲线只有一个波峰;L=1.6 nm时裂纹先以脆性解理的方式扩展,孔洞抑制裂纹扩展,孔洞周围发射位错,裂纹以尖端空洞形核、长大成微裂纹,最终微裂纹与主裂纹连接的方式扩展,能量曲线有多个峰值;L=4.8 nm时,裂纹初始扩展过程与L=1.6 nm时相似,后期未出现空洞形核、长大成微裂纹并与主裂纹结合的现象;另外孔洞距裂尖距离不同,发射第一个位错的方向不同。
关键词:γ-TiAl合金;分子动力学;位错;裂纹扩展;能量
0引言
随着航空航天工业的发展,轻质、高温结构材料成为研究者们关注的重点,而TiAl基合金作为新型结构材料其中之一,目前主要用于发动机用高压压缩机叶片、高压涡轮叶片、低压涡轮、过度导管梁、排气阀、喷嘴等[1]。γ-TiAl具有低密度、高比刚度、高温强度、良好的阻燃能力和抗氧化性等优点使其得到广泛应用[2-4]。γ-TiAl合金在制造和使用过程中本身存在的缺陷(例如微裂纹、孔洞等)对裂纹扩展过程存在显著影响,这些缺陷的进一步演化将造成材料的失效和破坏,因此,应当掌握这些缺陷的演化过程、机理以及缺陷之间的相互影响。分子动力学方法作为一种计算机模拟技术被国内外学者广泛采用,它能从微观层次通过原子间的相互作用力研究材料的变形和断裂过程。分子动力学的基本思想是在一定条件下,通过原子之间的相互作用势,求出每个原子所受的力,建立粒子系统的牛顿运动方程,利用数值方法求出每个时刻原子的位置和速度,进而得到粒子系统在相空间中随时间演化的轨迹,最后对计算结果进行长时间的统计平均,从而得到需要的宏观物理量。目前,已有大量学者用分子动力学方法从微观尺度研究裂纹和孔洞的演化过程。刘晓波等[5]用分子动力方法研究了铝的裂纹扩展过程,发现加载速率和初始裂纹长度影响体系拉开的时间。Wu等[6]采用分子动力学方法研究了不同温度下单晶镍中预置裂纹扩展时,裂纹尖端的应力分布和微观结构演化,发现温度不同,裂纹以不同的形式扩展。郭鹏等[7]用分子动力学方法研究了单晶硅预制裂纹的扩展过程,发现低温时裂尖形成环状结构,温度逐渐升高时出现母-子裂纹传播机制。Tang等[8]用分子动力学模拟了γ-TiAl单晶的空洞开裂过程,发现空洞开裂的原因,试件尺寸、空洞体积分数和应变影响初始屈服强度的大小。Li等[9]用分子动力学方法对裂纹尖端存在孔洞的单晶纳米铜的单轴拉伸过程进行了模拟,发现孔洞直径影响原子错排和裂尖钝化,单周加载引起了更多位错滑移的出现,且裂纹分支沿着孔洞的位置扩展的趋势更明显。刘光勇等[10]用分子动力学模拟了拉伸状态下纳米单晶铜中孔洞的力学行为,通过与无孔纳米单晶铜块体弹性能的比较,发现小孔使纳米单晶铜的弹性模量显著下降,位错滑移为其主要变形机制。
以上研究单独对裂纹和孔洞两种缺陷进行了分子动力模拟,研究了缺陷的演变过程,对两种缺陷之间的相互影响关系鲜有研究,而在实际材料中不止存在一种缺陷,往往是多种缺陷共存,缺陷之间也会产生影响,因此不仅要对每种缺陷进行研究,也要对缺陷之间的相互影响进行研究,才能更好的解释材料失效和破坏的机理。孔洞的不同形状对裂纹的扩展过程也会有影响,本文采用圆形孔洞,用分子动力学方法对γ-TiAl合金裂纹扩展过程和机理的研究尚不多见,而研究两种缺陷相互影响的文章就更少了。
针对以上研究的不足,本文在γ-TiAl单晶模型中预制了裂纹和孔洞两种缺陷,用分子动力学方法从微观尺度研究了不同孔洞位置对裂纹扩展的影响。
1计算模型和方法
1.1模型的建立
γ-TiAl合金的晶体结构与其它面心立方晶体的结构不同,具有L10型面心四方(fct)的晶体结构。
3种试样的原子模型由图1所示,均是在γ-TiAl合金中预制了(010)[100]中心裂纹,裂纹长度为12a,模型尺寸为120a×50b×6c,a为晶格常数,其中试样2和3中预制了半径为0.4 nm的孔洞,孔洞距裂尖的距离分别为1.6和4.8 nm。模拟温度为300 K,根据截断半径rcut的概念,即当两原子间距离超过rcut后,此两原子间相互作用力可以忽略不计,故设置边界条件时,使上下边界区的厚度大于原子间相互作用力的截断半径,为便于拉伸加载,在加载之前得到符合实际的“模拟试样”,减小试件中的残余应力,沿Y方向固定2a层原子,X和Y方向采用自由边界条件,Z方向周期性边界条件。X、Y、Z坐标轴分别对应γ-TiAl合金模型的[100]、[010]、[001]晶向。模拟分两个阶段进行:第一阶段,弛豫阶段,让体系各原子满足运动微分方程及初始与边界条件,而达到总势能最小的位置,整个体系在给定条件下弛豫120 ps即可使体系达到平衡状态;第二阶段,拉伸阶段,模型的下表面原子固定不动,通过给上表面原子施加1 m/s的恒定速度沿Y方向加载,模拟时间步为0.001 ps。

图1 γ-TiAl合金3种试样的原子模型
1.2EAM嵌入原子势
分子动力学以粒子系统为研究对象,系统中原子间相互作用用势函数来描述,而势函数的选择会影响模拟结果,因此,正确选择势函数及相关的参数对于模拟是非常重要的,EAM嵌入原子势[11]能很好得描述γ-TiAl体系原子间的作用力,故本文采用EAM嵌入原子势,其由两部分构成,即相互作用对势和嵌入能两部分。晶体的总势能可以表示为
(1)
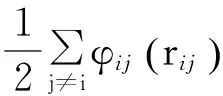
1.3计算方法
采用中心对称参数(CSP)测定局部晶格点阵无序程度和原子的位置,可以突出缺陷原子并且观察变形和断裂过程中缺陷的演化过程。中心对称参数P值的大小反映了缺陷类型,根据P值不同就可以区分不同类型的缺陷。采用式(2)所示的公式计算每个原子的CSP值[8]
(2)

用velocity-verlet算法[11]求解原子的运动轨迹,计算公式为
(3)
(4)
式中,r为原子的位置坐标;v为原子的速度;a为原子的加速度;t为原子运动时间;F为作用在原子上的力;m为相对原子质量。
2结果与分析
通过LAMMPS软件进行计算,OVITO软件进行可视化处理和结果分析得到给定条件下,不同孔洞位置下γ-TiAl合金裂纹扩展的原子轨迹图如图2~4所示。
体系预制中心微裂纹(无孔洞)时,不同时刻γ-TiAl合金的裂纹扩展图如图2所示。

图2 无孔洞时γ-TiAl合金的裂纹扩展图
同时预制裂纹和孔洞,L=1.6 nm时γ-TiAl合金的裂纹扩展图如图3所示。

图3 L=1.6 nm时γ-TiAl合金的裂纹扩展图
继续加载,孔洞周围不断有位错发射,t=1 914 ps时,裂纹继续沿[100]方向扩展,空洞形核,长大成微裂纹并与主裂纹串接、扩展直至材料完全断裂。
图4为同时含有预制裂纹和孔洞,L=4.8 nm时γ-TiAl合金的裂纹扩展图。

图4 L=4.8 nm时γ-TiAl合金的裂纹扩展图
从图4可得,裂纹扩展过程与L=1.6 nm时相似,孔洞的存在影响了裂尖的应力分布,而不同的孔洞位置对裂尖的应力分布也有影响,这就解释了孔洞与裂纹尖端的距离不同,发射第一个位错的方向也不同的原因。随着继续加载,孔洞周围不断有位错发射,在整个扩展过程中没有空洞出现。
3讨论
图5和6中的原子轨迹图分别为3个所标坐标对应时刻原子轨迹的局部放大图,其中裂尖与孔洞结合(a)以及第一个位错发射时刻(b)的应力如图所示,孔洞的存在会影响应力的分布,由于孔洞是圆形的,周围应力分布均匀,没有裂尖处的应力集中现象,所以当裂尖与孔洞结合后,裂纹会沿着没有孔洞的方向快速扩展。孔洞距离裂尖越远时,裂纹与孔洞结合以及发射第一个位错时的应力越小,这是因为应力在裂尖处集中,越靠近裂尖应力值越大。位错的形成造成应力集中,位错发射后应力释放,所以发射位错之后应力均呈下降趋势,不断发射的位错在边界塞积,使应力集中,因此应力值又会增大。

图5 L=1.6 nm时裂尖与孔洞结合以后及第一个位错发射前后应力随时间的变化曲线
Fig 5 Stress as function of the loading time atL=1.6 nm, crack tip combine with hole and stress change before/after the first dislocation emission
为了进一步研究不同孔洞位置对裂纹扩展的影响,提取拉伸过程中的总能量,将原子轨迹图与能量图结合进行分析。
从图7可以看出能量呈先增大后下降的趋势,这是因为随着加载的继续,γ-TiAl合金内部原子开始运动,动能增加,势能也从平衡态增大,使得总能量增大,此过程对应拉伸过程的弹性变形过程。在没有孔洞的模型中,裂纹以脆性解理的方式扩展直至材料断裂,只有弹性变形阶段,所以能量曲线只有一个能量峰值。L=1.6 nm和L=4.8 nm的能量曲线有多个能量峰值,结合原子轨迹图可知,拉伸过程中不断有位错发射,会消耗部分能量,使总能量下降,位错在运动的过程中会不断塞积,而位错的塞积又会使能量升高,升高到一定程度又会驱动位错的产生,使能量又开始下降,如此不断往复直到材料断裂为止,这就解释了能量曲线出现较大波动的原因。L=1.6 nm的能量轨迹图中能观察到明显的空洞形核、长大形成的微裂纹与主裂纹的汇集过程,所以在材料断裂之前,总能量曲线又出现一个能量最高峰。

图6 L=4.8 nm时裂尖与孔洞结合以后及第一个位错发射前后应力随时间的变化曲线
Fig 6 Stress as function of the loading time atL=4.8 nm, crack tip combine with hole and stress change before/after the first dislocation emission
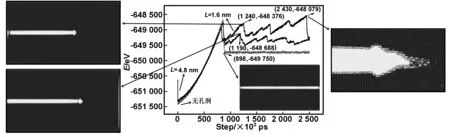
图7 不同孔洞位置时总能量随时间的演变过程
图8为不同孔洞位置对裂纹扩展影响的应力-应变曲线。
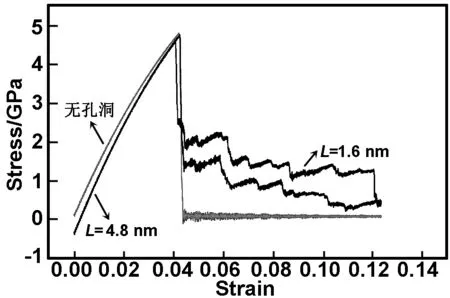
图8 不同孔洞位置对应的应力-应变曲线
Fig 8 Stress-strain curves at different hole position
从图8可以看出,在3种情况下,γ-TiAl合金均未出现屈服现象,符合其在室温条件下呈脆性的特性。无孔洞和L=1.6 nm时,应力峰值为4.8 GPa。L=4.8 nm时,应力峰值为4.6 GPa。有孔洞时,模拟过程出现了位错和空洞,位错成核需要一定的应力,微裂纹与孔洞距离较大的体系,二者汇合后,满足位错成核所需应力较小,位错成核较易,应力峰值较小;反之,微裂纹与孔洞距离较小的体系,二者汇合后,满足位错成核所需应力较大,位错成核较难,应力峰值较大。位错成核、迁移及空洞的出现将部分释放应力,使应力值随裂纹与孔洞距离的增大而减小,裂纹扩展过程中不断发射位错及位错塞积而形成曲线中的每一个波谷、波峰,当发射位错的密度足够高时位错释放应力而使应力-应变曲线下降,但不直接变为0;而无孔洞时,材料脆性断裂后应力直接变为0。由此,不同位置孔洞在裂纹扩展过程中,因发射位错的时间、数量、方式以及空洞成核等综合作用导致其对裂纹扩展的抑制作用不同,两种曲线的形状差异较大。
4结论
用分子动力学方法对γ-TiAl合金预制了裂纹和孔洞的裂纹扩展过程进行了研究,分析了不同孔洞位置对裂纹扩展的影响,得出以下结论:
(1)无孔洞时,裂纹以脆性解理的方式快速扩展直至材料断裂;能量曲线只有一个波峰。
(2)L=1.6 nm时,裂纹先以脆性解理的方式扩展,直至[100]方向材料断裂,孔洞的存在影响应力分布,抑制裂纹扩展;裂纹与孔洞结合后,孔洞周围有位错发射,孔洞变形,出现裂尖,裂纹以空洞形核、长大形成微裂纹并与主裂纹串接的方式继续扩展,能量曲线有多个波峰。
(3)L=4.8 nm时,初期裂纹扩展过程与L=1.6 nm时相似,后期没有出现空洞形核、长大成微裂纹的现象;能量曲线有多个波峰。
(4)孔洞的存在影响应力分布,而不同的孔洞位置也会影响应力分布,导致L=1.6 nm和L=4.8 nm时第一个位错的发射方向不同。
参考文献:
[1]Chen Yuyong, Su Yongjun, Kong Fantao.Research progress in preparation of TiAl interemetallic based compound[J]. Rare Metal Materials and Engineering, 2014,3:050.
陈玉勇, 苏勇君, 孔凡涛. TiAl 金属间化合物制备技术的研究进展[J]. 稀有金属材料与工程,2014,3:050.
[2]Clemens H, Mayer S.Design, processing, microstructure, properties, and applications of advanced intermetallic TiAl alloys[J]. Advanced Engineering Materials, 2013, 15(4):191-215.
[3]Marketz W T, Fischer F D, Clemen S H.Deformation mechanismsin TiAl intermetallics-experiments and modeling[J].International Journal of Plasticity, 2003, 19: 281-321.
[4]Clemens H, Smarsly W.Light-weight intermetallic titani-umaluminides-status of research and development[J].Advanced Materials Research, 2011, 278: 551-556.
[5]Liu Xiaobo,Xu Qingjun, Liu Jian. Molecular dynamics simulation of crack propagation behavior of aluminium[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1408-1403.
刘晓波,徐庆军,刘剑. 铝裂纹扩展行为的分子动力学模拟[J]. 中国有色金属学报,2014, 24(6):1408-1403.
[6]Wu W P, Yao Z Z. Molecular dynamics simulation of stress distribution and microstructure evolution ahead of a growing crack in single crystal nickel[J]. Theoretical and Applied Fracture Mechanics, 2012, 62: 67-75.
[7]Guo Peng, Wang Xueqing, Guo Zongbiao,et al.Molecular dynamics simulations of crack propagating along different orients in silicon[J]. Journal of Functional Materials, 2007, 38(4): 612-615.
郭鹏, 王雪青, 郭宗标, 等. 单晶硅预制初裂纹扩展行为的分子动力学研究[J]. 功能材料, 2007, 38(4): 612-615.
[8]Tang F L, Cai H M, Bao H W, et al. Molecular dynamics simulations of void growth in γ-TiAl single crystal[J]. Computational Materials Science, 2014, 84: 232-237.
[9]Li G, Hou X Q, Liu Z M. Influence of hole size on crack propagation mechanism of nano-single crystal copper[J]. Applied Mechanics and Materials, 2013, 328: 679-683.
[10]Liu Guangyong. Molecular dynamics simulations of tensile deformation of pores in the nano crystalline copper[J]. Journal of Atomic and Molecular Physics, 2004, 21(B04): 377-379.
刘光勇. 纳米单晶铜中孔洞拉伸变形的分子动力学模拟[J]. 原子与分子物理学报, 2004, 21(B04): 377-379.
[11]Potirniche G P, Horstemeyer M F, Wagner G J, et al. A molecular dynamics study of void growth and coalescence in single crystal nickel[J]. International Journal of Plasticity, 2006, 22(2): 257-278.
[12]Hu Wangyu, Shu Xiaolin. Theory ofembedded atom method and its application to materials science[M].Changsha:Hunan University Press,2003: 75-77.
胡望宇, 舒小林. 嵌入原子方法理论及其在材料科学中的应用[M].长沙:湖南大学出版社, 2003:75-77.
[13]Swope W C,Anderson H C, et al. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters[J]. Journal of Chemical Physics, 1982, 86:637-649.
Effectofholespositiononsinglecrystalγ-TiAlalloycrackpropagationbasedonmoleculardynamicssimulation
LUODechun1,2,RUIZhiyuan1,2,CAOHui1,2,CHENWenke1,YANChangfeng1,2
(1.MechanicalandElectricalEngineeringCollege,LanzhouUniversityofTechnology,Lanzhou730050,China;2.LanzhouUniversityofTechnologyDigitalManufacturingTechnologyandApplicationofKeyLaboratoryoftheChina’sMinistryofEducation,LanzhouUniversityofTechnology,Lanzhou730050,China)
Abstract:Moleculardynamicsmethodhasbeenappliedtotheresearchontheprocessofcrackpropagationofsinglecrystalγ-TiAl,theatomictrajectoryfigure,energyevolutionandtherelationshipbetweenstressandstrainwereobtainedaftertheholespositioneffecthadbeenstudied.Theresultsindicatethatthecrackpropagatesquicklyintheformofbrittlecleavageuntilthematerialfractureswhenthereisnoholemodelinthematerialandonlyonewavecrestcouldbediscoveredintheenergycurve;InthecaseofL=1.6nm,thecrackpropagatesintheformofbrittlecleavageatfirst.Then,thepropagationwasinhibitedbythehole,anddislocationsemitaroundthehole.Next,microcracksgrowupbyvoidnucleation.Finally,thecoalescenceandlink-upbetweenmicrocracksandthemaincrackwouldturnintothemainformofcrackspropagation,andmorewavecrestscouldbediscoveredinenergycurve;AsforL=4.8nm,theinitialprocessofcrackspropagationssimilartotheL=1.6nm,butvoidnucleation,growth,coalescenceandlink-upwiththemaincrackcouldnotappearatthelaterstage;also,theemissiondirectionofthefirstdislocationisdifferentwhencracktipshaveadifferentdistancefromholes.
Keywords:γ-TiAlalloy;moleculardynamics;dislocation;crackpropagation;energy
文章编号:1001-9731(2016)06-06136-06
* 基金项目:国家自然科学基金资助项目(51065014);甘肃省自然科学基金资助项目(148RJZA008);甘肃省高等学校科研资助项目(2014A-033)
作者简介:罗德春(1979-),男,甘肃兰州人,博士生,师承芮执元教授,主要从事材料机械强度、数字化制造技术的研究。
中图分类号:TG146;O77;TG131
文献标识码:A
DOI:10.3969/j.issn.1001-9731.2016.06.024
收到初稿日期:2015-10-01 收到修改稿日期:2016-01-10 通讯作者:曹卉,E-mail:1042126484@qq.com
