斜交曲线钢箱梁桥地震动力响应分析

李文华 彭泽友++滕文刚

摘要：为了研究桩土结构相互作用、斜交角等影响桥梁减隔震效果的影响因素，以某斜交曲线钢箱梁桥为工程背景，分别采用nD嵌固法和m法模拟桩基下部结构边界条件进行了结构地震动力时程分析与比较，并探讨了不同斜交角对曲线钢箱梁桥在地震作用下结构内力的影响，可为同类型桥梁设计提供参考依据。

关键词：斜交曲线钢箱梁；时程分析；地震动力响应；桩土结构作用

中图分类号：U448.21文献标志码：B 文章编号：1000033X（2016）06005604

0引言

中国位于世界两大地震带——环太平洋地震带和欧亚地震带之间，是一个强震多发的国家，随着社会经济的发展和科学技术水平的提高，工程结构减震控制技术在国内外得到了广泛应用[13]。在桥梁领域，目前减隔震技术已在中国大量推广，该技术是通过设置减隔震装置隔离上下部结构的地震作用，耗散地震能量，从而降低结构地震响应。现阶段关于影响桥梁减隔震效果的其他因素（桩土结构相互作用、斜交角等）的研究较少。因此，本文以某斜交曲线钢箱梁桥为背景进行地震动态时程分析，探讨桩土结构相互作用及斜交角对桥梁减隔震效果的影响，并给出合理的建议。

1动态时程分析法

动态时程分析法不仅可以考虑材料、边界等非线性因素，而且可以计算地震过程中每一瞬时结构的位移、速度和加速度反应，是目前桥梁减隔震动力分析中首选的分析方法。

2桥梁概况及结构建模

某斜交曲线钢箱梁桥工程位于京藏高速公路呼和浩特至包头段，桥梁全长469738 m，共计6联，跨径组合为（4×20 m）+（20 m+30 m+20327 m）+（213 m+30 m+213 m）+（3×20 m）+（51811 m+518 m）+（4×20 m），其中第5联上跨呼包高速；上部采用连续钢箱梁结构，桥位平面处于半径为260 m的左偏圆曲线上。

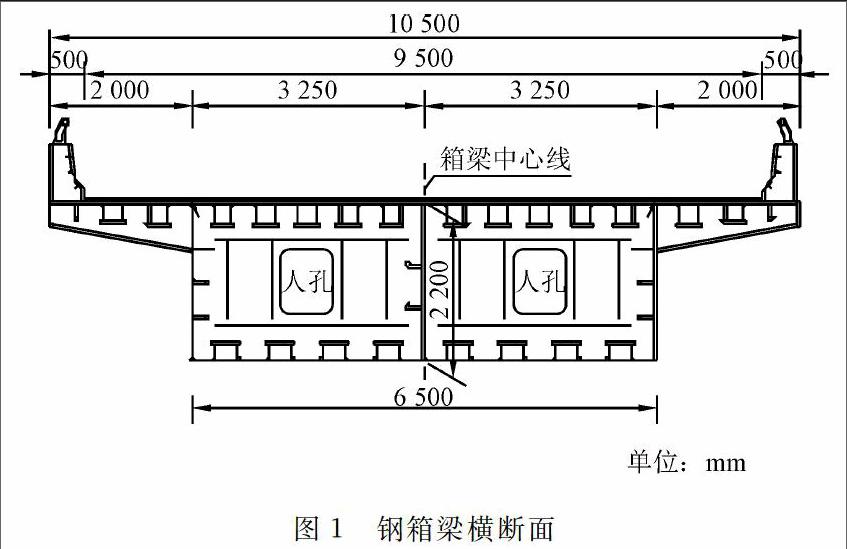
本桥标准段钢箱梁中心内轮廓高2.2 m，高跨比为1∶25；横断面为单箱双室直腹板全焊钢箱梁，设3道纵腹板，箱梁顶板宽10.5 m，底板宽6.5 m，悬臂长2 m。为了确保边支点支座在最不利荷载组合下具有足够的压力储备，边跨梁端填充铁砂混凝土压重。钢箱梁横断面如图1所示。

桥梁下部结构采用双柱式桥墩、钻孔灌注桩基础，桩接承台，柱径1.7 m，桩径1.5 m。

本文采用有限元分析软件Midas Civil建立该桥的空间有限模型，主梁和桥墩均采用三维梁单元，横隔板和二期铺装作为梁单元附加质量。

2.1桩基模拟

在动态时程地震响应分析中，地震反应不仅与地震动特性（峰值加速度、周期等）有关，还与结构本身的动力特性有关。下部结构边界条件常用的模拟方法有直接嵌固法、n倍桩径嵌固法（简称nD嵌固法，D为桩径）和m法，不同模拟方法对桥梁整体结构的刚度影响较大[4]。直接嵌固法是指在计算桥梁结构的地震影响时，不考虑桩基础的影响，直接在墩底固结。nD嵌固法是指部分考虑桩基础对桥梁结构力学响应的影响，即在地表或一般冲刷线下某一深度（通常取桩径整数倍）将桩基固结，嵌固深度H为

H=2.5/α（1）

α=5mb1EI（2）

式中：α为桩基变形系数；m为地基水平抗力系数的比例系数；b1为桩基础的计算宽度；EI为桩基础的刚度（E为桩身材料的弹性模量，I为桩身横截面的惯性矩）。

m法是指将桥梁结构与桩基础共同考虑，将桩周土体对基桩的作用模拟为沿深度变化的一系列弹簧，弹簧刚度按《公路桥涵地基与基础设计规范》（JTG D63—2007）中的m法要求取值[5]。需要注意的是，由于桩顶处土体对桩基础的力学行为影响很大，因此土体弹簧的设置一般以“上密下疏”为原则。

对于地震动力问题，由于直接嵌固法没有考虑桩基础对结构刚度的影响，难以反映结构实际的受力状态。故本文分别采用nD嵌固法和m法模拟下部结构边界条件，以研究不同边界条件模拟方法对结构受力分析的影响。nD嵌固模型与桩身土弹簧模型（m法模型）如图2所示。

2.2隔震支座力学模型

由于该桥所处地区地震烈度较高，故采用了桥梁减隔震设计来降低地震响应。减隔震支座选用了高阻尼隔震橡胶支座，在地震中通过高阻尼橡胶在水平方向的大位移剪切变形及滞回耗能吸收地震能量，隔离桥梁上、下部结构的地震运动，延长结构自振周期，减小地震作用力，从而实现减隔震功能，保障桥梁结构的抗震安全。

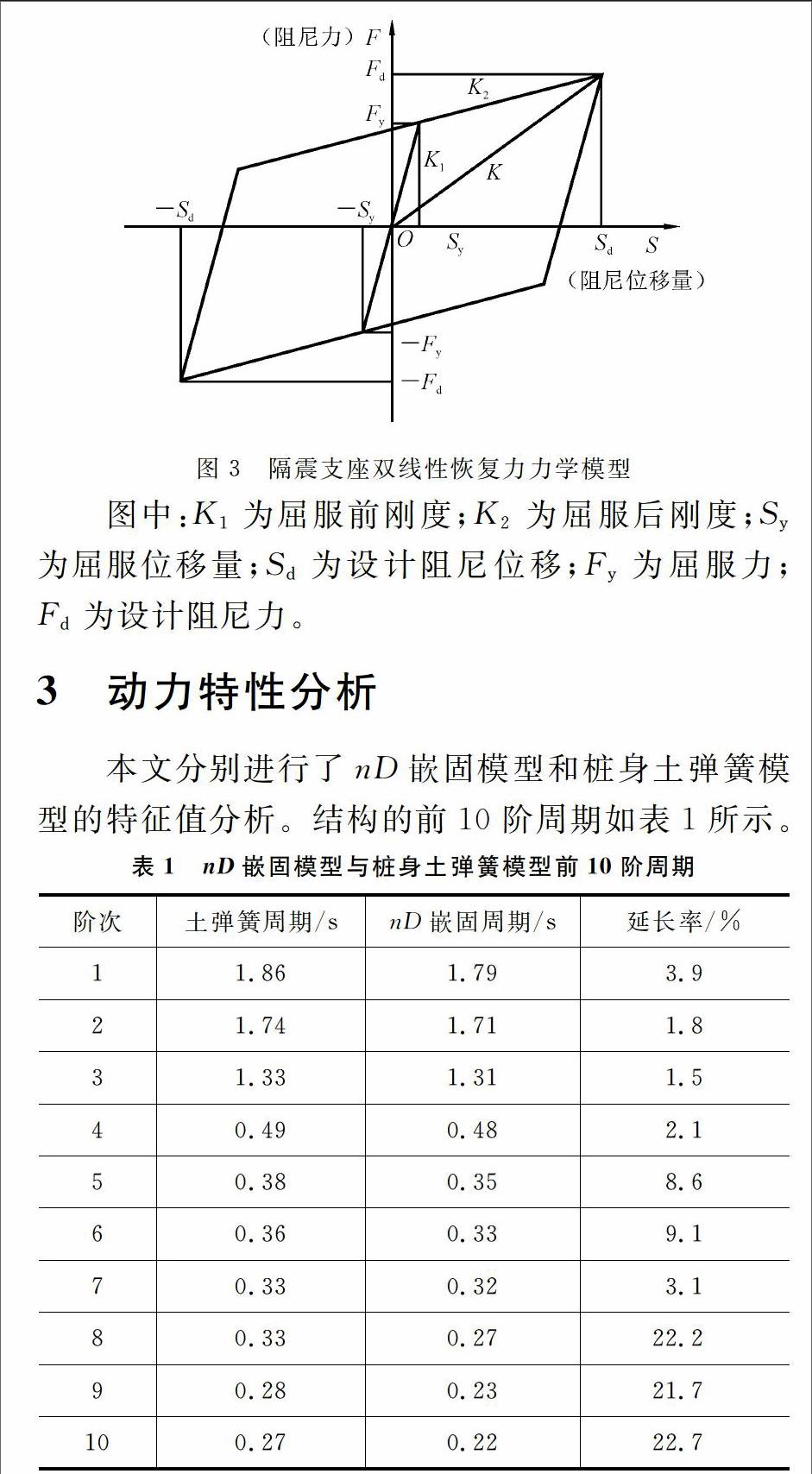
本支座力学模型为双线性模型，在非地震荷载即荷载较小时，支座处于未屈服状态，即一次刚度状态，刚度较大，各种荷载作用产生的位移较小，能够较好地满足正常应用；而在较大的地震作用下，支座将进入屈服状态，即二次刚度状态，刚度大幅减小，使得桥梁上下部结构能产生较大的相对运动，起到隔震消能作用。该支座力学模型如图3所示。

3动力特性分析

本文分别进行了nD嵌固模型和桩身土弹簧模型的特征值分析。结构的前10阶周期如表1所示。

由表1可知，桩身土弹簧模型的自振周期均大于nD嵌固模型的自振周期。前10阶振型中，自振周期最小的延长率达1.5%，最大的高达22.7%，即在考虑桩土效应后，整个体系的自振周期延长，自振频率减小。由于本桥所处地区地质条件较差，弹簧刚度按照规范给出的m值较小，而桩身土弹簧模型的桩长是nD嵌固模型桩长的数倍，故在m值较小的情况下，桩身土弹簧模型的柔性明显大于nD嵌固模型，即在地质条件较差的情况下，采用nD嵌固模型难以真实反映结构的自振周期。

4地震响应时程分析

根据《公路桥梁抗震设计细则》（JTG/T B0201—2008），本桥属于B类桥梁，地震动峰值加速度为0.15 g（g为重力加速度）。本文在进行结构动力地震响应分析时，按照瑞利阻尼模型选取结构阻尼，其中计算瑞利阻尼的第1阶振型为结构的基本振型，第2阶振型取参考质量率最大的振型。在一致激励输入下分别对nD嵌固模型和桩身土弹簧模型进行时程动力响应分析。

本文分别对比了桩身土弹簧模型与nD嵌固模型边界条件下结构的弯矩和剪力，结果如表2、3所示。

由表2、3可知，与nD嵌固法相比，采用桩身土弹簧模拟桩土效应时，在地震力作用下，墩底弯矩和剪力都相应减小，尤其是中墩横桥向弯矩，2种边界条件下弯矩差值都超过10%。由于采用nD嵌固法模拟边界条件时，结构整体刚度偏大，计算结果偏于保守，设计人员应予以重视。

5中墩斜交角对桥梁地震响应的影响

由于被交路的限制，本桥梁中墩为斜交布置。为了分析中墩斜交角对桥梁地震响应的影响，建立中墩斜交角θ分别为20°、40°、70°和90°的桩身土弹簧模型，进行动力时程地震响应分析[7]。分析结果如表4、5及图4、5所示。

从表4、5及图4、5可知，随着斜交角度不断增大，过渡墩顺桥向弯矩逐渐增大，横桥向弯矩逐渐减小，且顺桥向与横桥向间弯矩差值逐渐增大；而中墩顺桥向弯矩逐渐减小，横桥向弯矩逐渐增大，且顺桥

向与横桥向弯矩间弯矩差值逐渐减小，当斜交角为90°时，中墩顺桥向与横桥向弯矩差值达到最小。

由此可知，对于过渡墩弯矩控制设计的桥梁来说，中墩斜交角度增大对于桥梁抗震是不利的。由于中墩斜交角度的增大，过渡墩顺桥向及横桥向弯矩差值逐渐增大，为了抵抗顺桥向弯矩，桥墩截面需相应加大，而横桥向弯矩又相应较小，是不经济的。

对于中墩弯矩控制设计的桥梁，中墩斜交角度增大对于桥梁抗震是有利的，因为中墩顺桥向及横桥向弯矩的差值将随斜交角度的增大而减小，由此而得的中墩截面尺寸较为优化，具有较好的经济性。

6结语

本文以某斜交曲线钢箱梁桥为工程背景，分析比较了采用nD嵌固法和m法模拟桩土效应时，结构的地震内力响应，并探讨了中墩斜交角对曲线钢箱梁桥地震内力的影响，主要结论如下。

（1）在地质条件较差的情况下，采用nD嵌固模型难以真实反映结构的自振周期。由于m值较小，而桩身土弹簧模型的桩长是nD嵌固模型桩长的数倍，故在与本文所述实例桥类似的情况下，桩身土弹簧模型的柔性明显大于nD嵌固模型，采用nD嵌固法计算的结构自振周期将明显小于采用m法计算的结构自振周期。

（2）采用m法模拟桩土效应时，在地震力的作用下，本工程实例桥墩底弯矩及剪力均小于采用nD嵌固法的计算结果，且两者差值较大，在设计中应引起足够重视。

（3）对于过渡墩弯矩控制设计的桥梁，中墩斜交角度增大对于桥梁抗震是不利的；对于中墩弯矩控制设计的桥梁，中墩斜交角度增大对于桥梁抗震是有利的。故在具体设计中，应综合比较利弊，在条件允许的情况下，优化桥梁结构设计，提高结构的安全性及经济性。

参考文献：

[1]范立础.桥梁抗震[M].上海：同济大学出版社，1997.

[2]范立础.桥梁减隔震设计[M].上海：同济大学出版社，2001.

[3]谢旭，桥梁结构地震响应分析与抗震设计[M].北京：人民交通出版社，2006.

[4]刘健新.汶川地震桥梁破坏及中外桥梁抗震设计规范对比[J].筑路机械与施工机械化，2010，27（11）：2023.

[5]JTG D63—2007，公路桥涵地基与基础设计规范[S].

[6]JTG/T B0201—2008，公路桥梁抗震设计细则[S].

[7]刘荣桂，周士金，许飞，等.CFRP索斜拉试验桥动态测试与地震响应分析[J].长安大学学报：自然科学版，2009，29（6）：4753.