用机械能守恒定律解连接体问题

龚茂盛

用机械能守恒定律解连接体问题中，学生最大的障碍是找不到连接体中两物体的速度关系.其实常见连接体的问题，通常可按二者的速度关系分为三种模型，抓住各自模型的特征，一般问题均可迎刃而解.

模型一：如图1

特征：两物体在相等时间内运动位移始终相等，因此任何时刻两物体速度大小始终相等.

【典例1】一根细绳不可伸长，通过定滑轮，两端系有质量为M和m的小球，且M=2m，开始时用手握住M，使M与离地高度均为h并处于静止状态.求：（1）当M由静止释放下落h高时的速度.（2）设M落地即静止运动，求m离地的最大高度.（h远小于半绳长，绳与滑轮质量及各种摩擦均不计）

解：在M落地之前，系统机械能守恒

（M-m）gh=1/2（M+m）vv=

M落地之后，m做竖直上抛运动，由机械能守恒有：1/2mv=mgh/h/=h/3

离地的最大高度为：H=2h+h/=7h/3

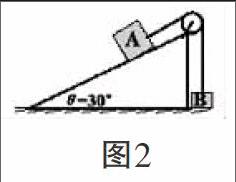
【变式题】如图所示，一固定的楔形木块，其斜面的倾角θ=30°，另一边与地面垂直，顶上有一定滑轮.一柔软的细线跨过定滑轮，两端分别与物块A和B联结，A的质量为4m，B的质量为m，开始时将B按在地面上不动，然后放开手，让A沿斜面下滑而B上升.（物块A与斜面间无摩擦）设当A沿斜面下滑S距离后，细线突然断了.求物块B上升离地的最大高度H.

特征：两物体在相等时间内转过的角度始终相等，因此任何时刻两物体角速度大小始终相等，线速度的大小与各自转动半径成正比.

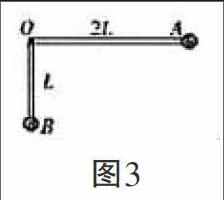
【典例2】如图3所示，质量分别为2m和3m的两个小球固定在一根直角尺的两端A、B，直角尺的定点O处有光滑的固定转动轴，AO、BO的长分别为2L和L，开始时直角尺的AO部分处于水平位置而B在O的正下方，让该系统由静止开始自由转动，求（1）当A达到最低点时，A小球的速度大小v；（2）B球能上升的最大高度h.（不计直角尺的质量）

解：直角尺和两个小球组成的系统机械能守恒

【变式题】如图4，质量分别为m和2m的两个小球A和B，中间用轻质杆相连，在杆的中点O处有一固定转动轴，把杆置于水平位置后释放，在B球顺时针摆动到最低位置的过程中（ ）

A.B球的重力势能减少，动能增加，B球和地球组成的系统机械能守恒

B.A球的重力势能增加，动能也增加，A球和地球组成的系统机械能不守恒

C.A球、B球和地球组成的系统机械能守恒

D.A球、B球和地球组成的系统机械不守恒

【分析解答】B球从水平位置下摆到最低点过程中，受重力和杆的作用力，杆的作用力方向待定.下摆过程中重力势能减少动能增加，但机械能是否守恒不确定.A球在B下摆过程中，重力势能增加，动能增加，机械能增加.由于A+B系统只有重力做功，系统机械能守恒，A球机械能增加，B球机械能定减少，因此B，C选项正确.

模型三：如图5

特征：用绳杆相牵连的物体，在运动过程中，其两物体的速度通常不同，但物体沿绳或杆方向的速度分量大小相等发，即：Vcos30=Vcos60.

【典例3】如图6，一半径为R的半圆形竖直圆柱面，用轻质不可伸长的细绳连接的A、B两球，悬挂在圆柱面边缘两侧，A球质量为B球质量的2倍，现将A球从圆柱边缘处由静止释放，如图所示，已知A始终不离开球面，且细绳足够长，若不计一切摩擦.

（1）求A球沿圆柱面滑至最低点时速度的大小；

（2）求A球沿圆柱面运动的最大位移.

【分析解答】设A球沿圆柱面滑至最低点时速度的大小为v，则据机械能守恒定律可得：2mgR-mgR=2mv+mv①

又因为v=v②解得v=2③

（2）当A球的速度为0时，A球沿圆柱面运动的位移最大，设为s，据机械能守恒定律可得：2mg-mgs=0④

解得s=R⑤

总结：①对于多个物体组成的系统要注意判断物体运动过程中，系统的机械能是否守恒；

②注意两物体间的瞬时速度关系；

③列机械能守恒方程时，一般选用△EK=-△EP 。