“三步法”在球柱处方转环曲面处方中的运用
2016-07-15周正宏何国花
周正宏+何国花
【摘 要】在《眼镜光学技术》这门课程的教学过程中,有一难点内容为环曲面透镜的转换,即将球柱处方转换为环曲面处方,学生学习完课本上的方法后出现理解不透,记不住,容易出错等问题,针对这个问题,我总结了一套有效又记忆深刻的方法,简称为“三步法”,只需要经过三步后,就可将球柱镜处方轻松转换成环曲面处方。
【关键词】转换;球柱处方;环曲面处方
在《眼镜光学技术》这门课程的教学过程中,有一难点内容为环曲面透镜的转换,即将球柱处方转换为环曲面处方,教科书上的转换步骤为:若已知基弧,则正交弧=基弧+柱面成分,球弧=球面成分-基弧,直到基弧、正交弧及球弧后即可写出环曲面的处方,此种转换方式可行也正确,但是需要记得这两个计算等式才行,而学生在学习这块内容时,对于这种需要纯粹记忆的等式最是头疼,往往上一节课刚学完,下一节课就给忘了,因为学生能够短暂的记得刚学的内容,而不能够理解这块内容,所以就算短时间内会转换,时间长了就忘了。
怎样能让学生长时间记住正确且有效的环曲面转换方法呢,在长期教学过程中,我总结了一套有效又记忆深刻的方法,用这套方法完成环曲面处方的转换只需要三步,所以简称为“三步法”,第一步还原光学十字,第二步图形填空,第三步写环曲面处方,经过这三步后球柱镜处方就转换成环曲面处方了。下面我们以例1进行演示。
例1:将球柱镜处方-4.00DS/-2.00DC×180转换为基弧为-9.00D的环曲面形式。
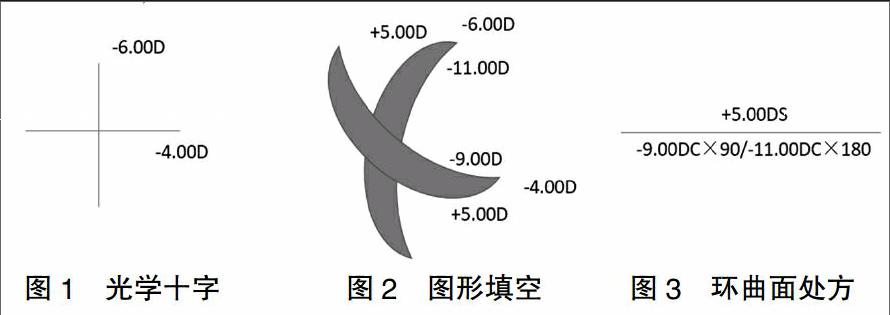
第一步还原光学十字,将-4.00DS/-2.00DC×180还原为光学十字得到垂直方向上屈光力为-6.00D,水平方向屈光力为-4.00D(见图1所示)。
第二步图形填空,画出一个镜片前、后表面垂直与水平方向的模型,将垂直方向屈光力-6.00D与水平方向-4.00D分别写在垂直与水平方向上,已知要求转换后基弧为-9.00D,基弧的方向为屈光力小的那个方向,所以转换后基弧在水平方向,再加上转换后的基弧为一负度数,所以-9.00D应该在后表面的水平方向,而水平方向总的屈光力不变为-4.00D,故前表面水平方向屈光力为+5.00D,基弧在后表面,那前表面就是球弧,所以前表面垂直方向屈光力也是+5.00D,而垂直方向总的屈光力为-6.00D,所以可以知道后表面垂直方向屈光力为-11.00D,这样前、后表面垂直水平方向屈光力就都出来了(见图2所示)。
第三步写环曲面处方,将前后表面的参数写成环曲面处方的形式,前表面为分子,后表面为分母,+5.00DS/-9.00DC×90-11.00DC×180(见图3所示)。
该方法在转换时有一个特殊情况要注意,就是当转换前的球柱镜处方与转换后的环曲面处方的基弧符号相反时,基弧的方向应该取屈光力大的那个方向,除了这个情况外都可按照上面的“三步法”进行转换,下面我们将举一个例子说明特殊情况下的处方转换。
例2:将球柱镜处方-4.00DS/-2.00DC×180转换为基弧为+9.00D的环曲面形式。
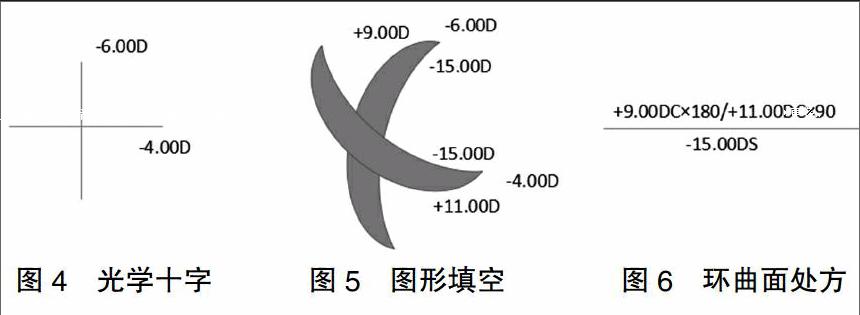
第一步还原光学十字,将-4.00DS/-2.00DC×180还原为光学十字得到垂直方向上屈光力为-6.00D,水平方向屈光力为-4.00D(见图4所示)。
第二步图形填空,与例1相同,画出一个镜片前、后表面垂直与水平方向的模型,将垂直方向屈光力-6.00D与水平方向-4.00D分别写在两方向上,已知要求转换后基弧为+9.00D,因为球柱镜处方屈光力小的为-4.00D,而转换后的基弧要为+9.00D,两者的符号相反,为一正一负,所以在转换时基弧的应该取屈光力大的那个进行转换,所以此时转换后基弧应该在垂直方向上。现在转换后基弧为+9.00D,为一正度数,所以屈光力应该在前表面的垂直方向上,基弧在前表面,故前表面垂直方向屈光力为+9.00D,而垂直方向总的屈光力不变为-6.00D,那后表面就为一球弧,所以后表面屈光力就是-15.00DS,而垂水平向总的屈光力为-4.00D,所以可以知道前表面水平方向屈光力为+11.00D,这样前、后表面垂直水平方向屈光力就都出来了(见图5所示)。
第三步写环曲面处方,将前后表面的参数写成环曲面处方的形式,前表面为分子,后表面为分母,+9.00DC×180+11.00DC×90/-15.00DS(见图6所示)。
运用此种方法学生学习本节内容印象深刻,掌握起来比较简单,关键是在学习的过程中,学生能更好的理解一个屈光不正的处方是怎样转换成为成品镜片的。
[责任编辑:杨玉洁]