角位置测量误差补偿方法研究*

张　功，张晓飞，王昱峰，曹玉梅，赵　健

(北京航天计量测试技术研究所，北京 100076)



角位置测量误差补偿方法研究*

张功，张晓飞，王昱峰，曹玉梅，赵健

(北京航天计量测试技术研究所，北京 100076)

摘要:为提高精密转台测角精度，提出了两种测角误差补偿算法. 在分析了多面棱体校准原理基础上提出了基于误差平均的线性补偿方法，并给出了补偿计算表达式. 另一种方法通过分析测角误差具有周期特性，利用傅里叶级数对误差值进行计算求解到谐波幅值较大的阶次进行反向补偿. 通过实验案例对两种算法的补偿效果进行了验证. 结果表明： 两种补偿算法均可大幅提高转台位置精度，可满足项目技术协议中对角位置精度的要求，最后针对两种方法的优缺点一并进行了论述.

关键词:精密转台； 位置精度； 误差补偿； 角位置测量

精密转台是一种专用测试设备，它可为被测惯性导航仪表及导航系统提供精确的方位和速率等输入信号. 高精度是转台主要特征，其精度的保证需要机械轴系、位置反馈部件及控制系统配合完成. 控制系统中的补偿算法可对位置误差进行修正，大幅提高转台位置精度，在工程设计中得到广泛应用. 精密转台通常采用光电编码器作为位置反馈器件，光电编码器具有分辨率高、抗干扰能力强、机械寿命长等优点. 控制系统采用基于RTX的实时控制软件，在一个标准中断周期(通常为1 ms)完成对编码器的数据采集及补偿运算工作.

关于编码器误差补偿研究，文献[1]对当前补偿技术进行了现状分析； 文献[2]应用粒子群算法对补偿模型进行了参数辨识； 文献[3]分析了光栅偏心对转台角位置精度的影响； 文献[4，5]利用三角函数展开对测角误差补偿进行了研究； 文献[6]利用傅里叶级数展开对平行双关节坐标测量机误差进行了研究. 本文介绍了两种位置误差补偿方法，一种是基于误差平均的线性补偿方法，另一种是基于函数傅里叶展开的谐波补偿方法，通过一个实验案例采用两种方法展示了补偿效果.

1光电编码器原理简介

光电编码器由圆光栅盘和光电检测装置组成，主要技术包括光电扫描及测角细分. 光电扫描原理是用透射光生成信号： 两个具有相同栅距的光栅尺和读数头相对运动，这种光栅相互作用的光学现象称为莫尔条纹. 光电池将光强变化转化成正弦电信号，电信号经过转换电路处理可得到被测轴的转角或速度信息. 由于光栅测角具有的正弦性会导致误差分布具有明显的周期特性，这为后续误差谐波补偿提供了依据. 对精密转台角位置的计量通常采用光电自准直仪与多面棱体配合的方式. 多面棱体是一种高准确度的角度计量标准器具，常用的有8，9，12，17，23，24，36面等不同规格.

2线性补偿方法

假设光电编码器圆光栅全周有N条刻线，光栅每相对移动一条刻线，产生的正弦信号相应移动一个周期，即代表角度移动了360°/N，输出的正弦信号被电路转换成与此正弦信号一致的周期性脉冲信号，对脉冲信号进行计数，即可获得所测角度的“大数”，不足一个周期的角度值“小数”部分则必须进行细分[7]. 采用质数面多面棱体对光栅测量时，可得到一个栅距内若干个细分量误差，以这些细分误差进行线性化计算可获得整周范围内的误差补偿值.

以23面棱体为例，面数23不能为360整除，其产生的小角度部分可表征出一个栅距内的角度信息. 如某5 000线码盘，其一格栅距为0.072°. 23面棱体第i面角度值为360·i/23, (i=1,2,…,23). 第i面不足一个栅距的角度

(1)

式中： 符号[]表示向零取整运算. 测量时设某角度为θ，数值大小处于23面棱体的第i面角度与第i+1面角度之间，如图1 所示.

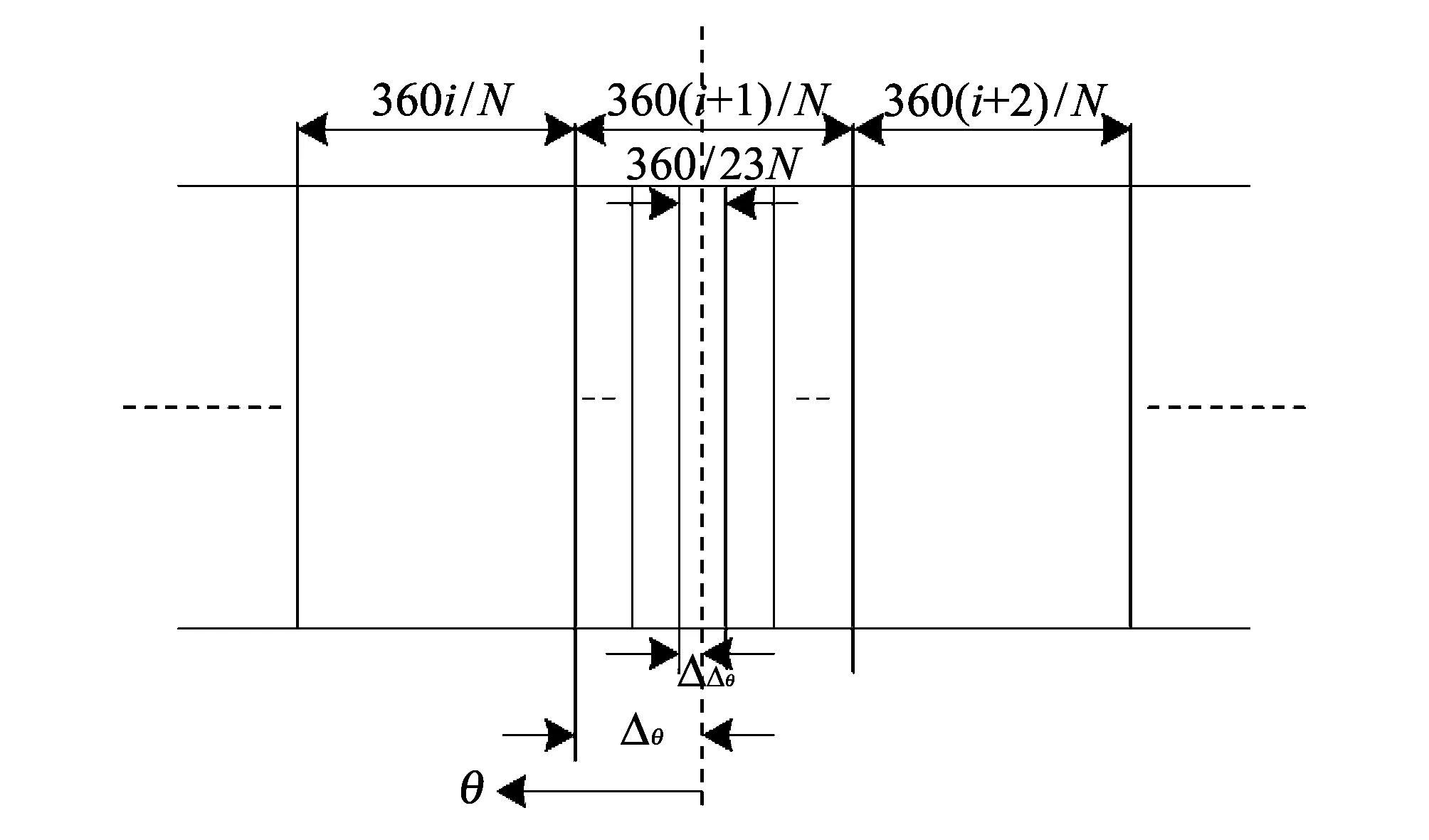
图1　23面棱体测量角度示意图Fig.1　Measuring angle with 23 polyhedron diagram

角度θ处于一个栅距内的角度为Δθ； 同理，角度Δθ处于一个细分范围内的角度为ΔΔθ，两个小角度如式(2)所示.

(2)

线性补偿利用误差平均思想以23点测量数据为采样点作线性化计算，但需要注意的是，按角度递增拟合出的折线应是唯一的，故全周范围内的23个测试数据应首先按各自所对应的细分条数进行排序. 对于线数为N的圆光栅，棱体第i面对应的细分排序l由式(3)表示.

(3)

23个采样点经排序后获得的线性补偿值

(4)

式中：ai,ai+1为第i面与第i+1面的测量值扣除棱体自身偏差并经排序后的数值. 按式(4)将误差修正式写入控制程序便可实现对测角误差的补偿.

3谐波补偿方法

由第一部分分析可知，圆光栅测角误差具有周期特性，因此可利用谐波分析法对误差数据进行处理. 误差函数的谐波展开如式(5)所示.

(5)

式中：a0,ak,bk为各次谐波系数；ck,φk为各次谐波幅值与相位. 工程应用中容易得到的是误差离散采样值而非连续准确的数学描述. 业已证明[8]，由离散采样序列可通过式(6)得到函数展开后的各次系数.

(6)

当采用23面棱体对转台进行校准时，因23面棱体是将整周角度23等分，故谐波系数需计算到11阶[9]. 设测量的一组误差数据为E=[E(θ1),E(θ2),…,E(θ23)]T，根据式(6)建立方程组

(7)

设

则式(7)矩阵形式为

E′=AX.

(8)

求解此矩阵方程便可得出各阶谐波系数值. 观察式(8)可发现，式(8)的系数矩阵行列数值并不相等，属超定方程组，得到的是其最小二乘解，解的形式如式(9)所示[10].

(9)

通过相位大小选出对误差影响较大的阶次，从而得到谐波补偿的数值表达式. 将表达式写入控制程序中便可实现对测角误差的补偿.

4实验案例

参照GJB1801-93方法104采用23面棱体、光电自准直仪对某精密转台进行位置精度测试，如图2 所示. 圆光栅线数为36 000线. 经正反向若干次测量，4组测量误差曲线如图3 所示.

图2　某型精密转台校准示意图Fig.2　Precision turntable calibration diagram

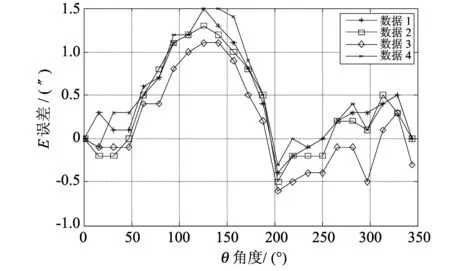
图3　4组误差数据曲线Fig.3　Four error data sets curve

由图3 可见，4组测量误差趋势大体一致. 将这几组误差数据代入式(8)计算得11阶内各次谐波系数如表1 所示.

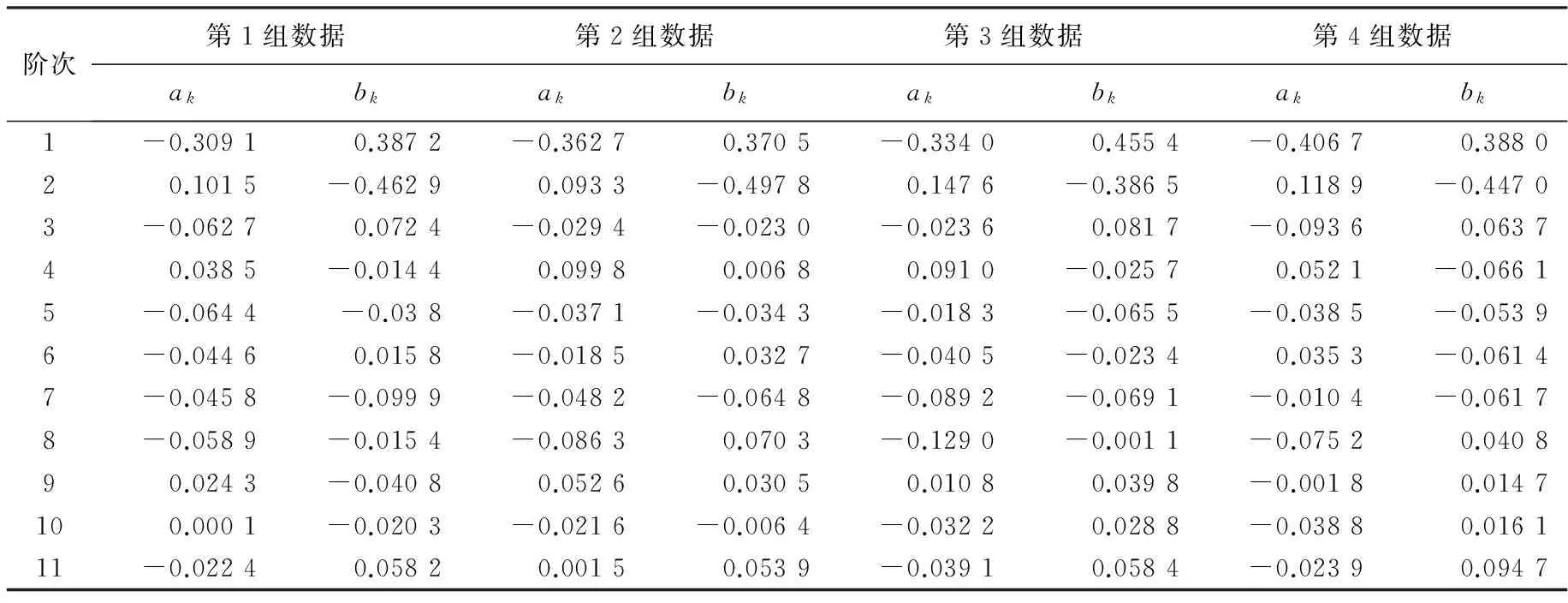
表1　4组误差数据11阶内谐波系数列表

由表1 中数据按式(5)计算得4组谐波幅值如图4 所示. 观察图4 中4组数据的幅值大小可以发现，对误差影响较大的主要有1次、2次及8次谐波，通过程序对误差信号进行反向补偿. 取这几次测量所得各次谐波系数的平均值，则包含这几次谐波量的全误差补偿公式如式(10)所示.

(10)

采用式(4)及式(10)补偿后再测量，前后结果如图5 所示，谐波补偿后位置精度为(+0.4″,-0.4″)； 线性补偿后位置精度为(+0.2″,-0.2″). 可见，两种算法均可使测量误差大幅减小，达到了项目技术协议中角位置精度不大于±1″的要求.

两种方法的实现也存在各自特点. 谐波补偿理论计算复杂，补偿计算需在控制程序中断周期内完成，且含有多个三角函数，对控制计算机性能要求较高，但该方法可避免对测量所得数据的繁琐排序过程； 线性补偿计算量小且编程易实现，但需对测量数据进行排序才能获得唯一的拟合折线.

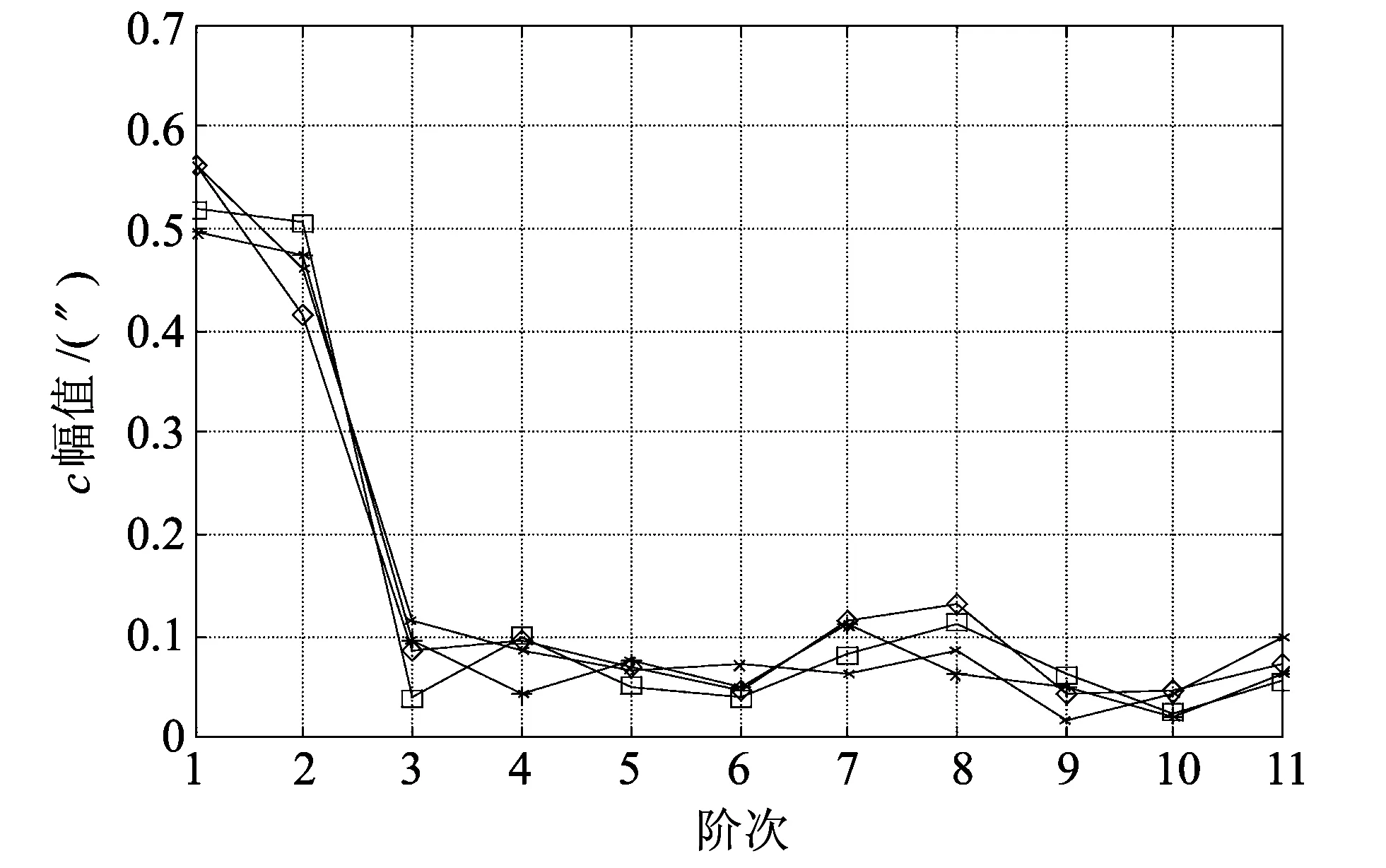
图4　4组误差数据11阶内谐波幅值示意图Fig.4　11th harmonic amplitude diagram of the four error data

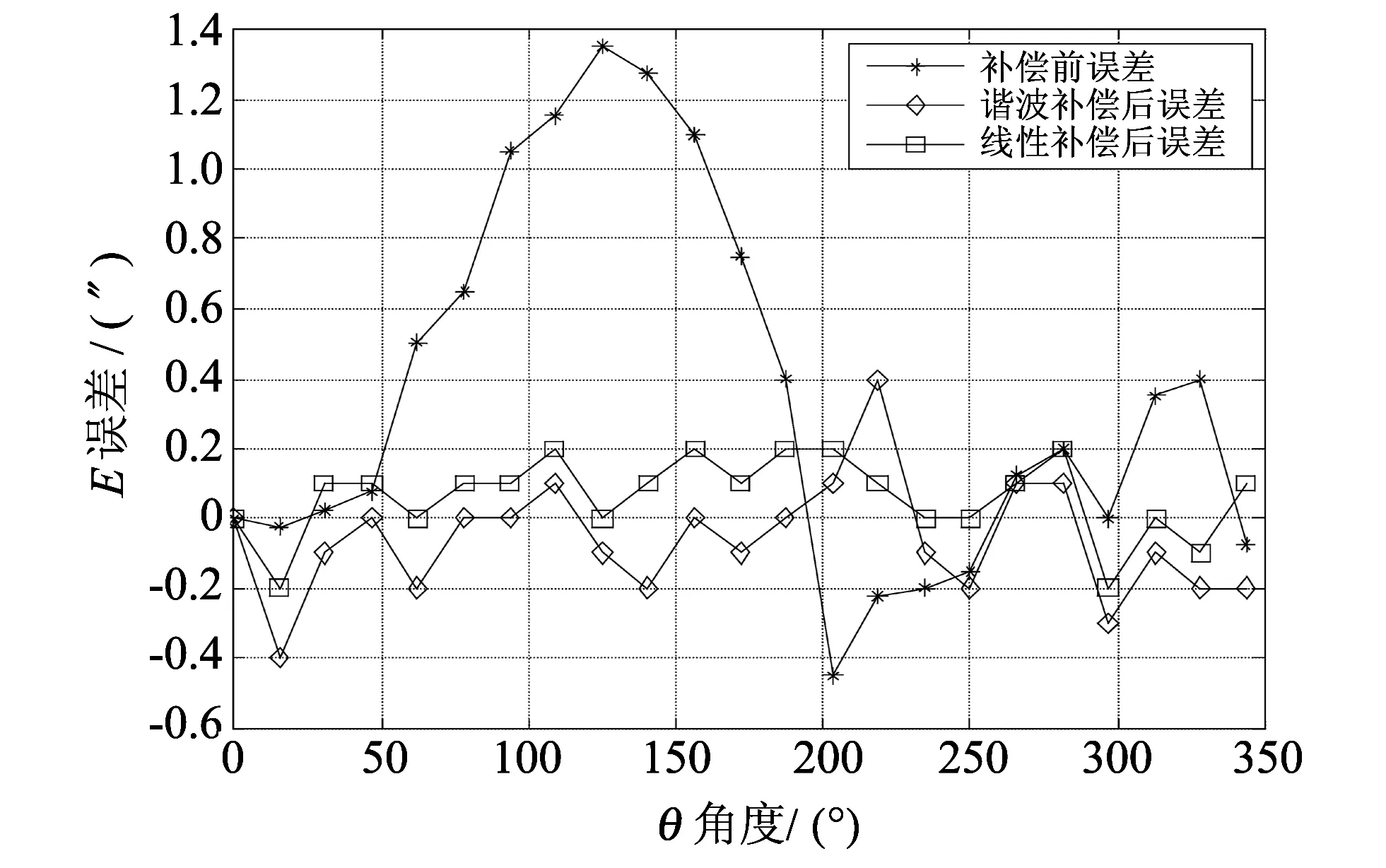
图5　补偿前后误差数据示意图Fig.5　Error data before and after compensation diagram

5结束语

惯导测试设备对位置精度的要求越来越高，在保证精度的措施中，软件补偿因其具有易实现、效果明显、成本耗费小等优点得到广泛应用. 本文介绍了两种位置误差补偿算法，并通过实际案例验证了其可行性，对补偿算法的研究具有一定的参考价值.

参考文献：

[1]高旭，万秋华，王树洁. 光电轴角编码器信号补偿技术的研究进展[J]. 光电子技术，2013，33(2)： 131-136.

Gao Xu,Wan Qiuhua,Wang Shujie. Development of signal compensation technology for photoelectric rotary encoder[J]. Opto Electronic Technology，2013，33(2)： 131-136. (in Chinese)

[2]高贯斌，王文，林铿. 圆光栅角度传感器的误差补偿及参数辨识[J]. 光学精密工程，2010，18(8)： 1766-1771.

Gao Guanbin，Wang Wen，Lin Keng. Error compensation and parameter identification of circular grating angle sensors[J]. Optics and Precision Engineering，2010，18(8)： 1766-1771. (in Chinese)

[3]糜小涛，高胜英. 圆光栅偏心对仿真转台角位置精度的影响[J]. 长春理工大学学报(自然科学版)，2014，37(3)： 9-12.

Mi Xiaotao，Gao Shengying. Effect of eccentric of circular gratings on angular position accuracy of simulator[J]. Journal of Changchun University of Science and Technology(Natural Science Edition)，2014，37(3)： 9-12. (in Chinese)

[4]赵人杰，马文礼. 利用误差谐波补偿法提高金属圆光栅测角精度[J]. 仪器仪表用户，2009，16(3)： 69-71.

Zhao Renjie，Ma Wenli. Improving the accuracy of new-type encoders using error harmonic compensation[J]. Electronic Instrumentation Customer，2009，16(3)： 69-71. (in Chinese)

[5]吴敏. 惯性测试转台的圆光栅测角模块和摩擦补偿研究[D]. 哈尔滨： 哈尔滨工业大学，2011.

[6]于连栋，丁洋，程文涛. 平行双关节坐标测量机圆光栅测角误差补偿技术[J]. 南京理工大学学报(自然科学版)，2009，33(5)： 660-662.

Yu Liandong，Ding Yang，Cheng Wentao. Compensation of angle measurement error of circular gratings for parallel dual-joint coordinate measuring machine[J]. Journal of Nanjing University of Science and Technology(Natural Science)，2009，33(5)： 660-662. (in Chinese)

[7]李怀琼，陈钱，王钰. 新型光栅信号数字细分技术及其误差分析[J]. 计量学报，2001，22(4)： 281-282.

Li Huaiqiong，Chen Qian，Wang Yu. A new digital subdividing technique for grating signal and its error analysis[J]. Acta Metrologica Sinica，2001，22(4)： 281-282. (in Chinese)

[8]何天祥. 周期信号各参数的离散采样测量法[J]. 航空计测技术，1997，17(3)： 3-4.

He Tianxiang. Discrete sample measuring method of parameters for periodic signal[J]. Aviation Metrology&Measurement Technology，1997，17(3)： 3-4. (in Chinese)

[9]姚景风. 谐量混杂的探讨[J]. 工具技术，1983(7)： 36-40.

Yao Jingfeng. Discussion on harmonic quantity[J]. Tool Engineering，1983(7)： 36-40. (in Chinese)

[10]熊有伦. 精密测量的数学方法[M]. 北京： 中国计量出版社，1989.

Study on Error Compensation of Angular Position Measurement

ZHANG Gong，ZHANG Xiaofei，WANG Yufeng，CAO Yumei，ZHAO Jian

(Beijing Aerospace Institute for Metrology and Measurement Technology，Beijing 100076, China)

Abstract:In order to improve the measurement accuracy of the precision turntable, two kinds of error compensation algorithm were put forward. Linear compensation method based on the average error was proposed after analyzing the prism calibration principle and compensation calculation expression was also given. After finding the angle measurement error has a periodic characteristic, error values were calculated by using Fourier series and used the larger harmonic amplitude to compensate reversedly. The effects of the two compensation algorithms was validated though experiments. The results shows that the two compensation algorithm could substantially increase the position accuracy of the turntable, which could meet the angular position accuracy requirementsin the technical agreement. At the end, The advantage and disadvantage of these two methods are also listed in this paper.

Key words:precision turntable; position accuracy; error compensation; angular position measurement

文章编号:1671-7449(2016)04-0353-05

收稿日期：2016-03-07

基金项目：国防军工计量科研计划资助项目(JTAL11607)

作者简介：张功(1985-)，男，工程师，主要从事惯导测试设备研制与测试方法研究.

中图分类号:TP394.1

文献标识码:A

doi:10.3969/j.issn.1671-7449.2016.04.012