行星轮系渐开线变位齿轮时变啮合刚度数值计算

岳喜铮，丁问司，丁　康， 曾智杰

(华南理工大学 机械与汽车工程学院, 广州　510641)



行星轮系渐开线变位齿轮时变啮合刚度数值计算

岳喜铮，丁问司，丁康， 曾智杰

(华南理工大学 机械与汽车工程学院, 广州510641)

摘要：齿轮啮合刚度的时变性是齿轮产生振动的主要原因，对齿轮时变刚度进行求解计算具有重要的意义。基于正变位行星轮系外齿轮齿形几何参数的计算方法，根据内外齿轮齿形的不同，推导出内齿轮齿形几何参数计算过程。利用石川公式中轮齿变形计算公式和刚度求解公式，通过Matlab编程求得正变位行星轮系内外啮合时变啮合刚度曲线，并与Weber能量法计算结果进行对比，结果表明：静态刚度最大误差为3.7%，不考虑幅值为很小值时的动态刚度，前4阶谐波幅值最大误差约为9.1%，精度满足要求，可以为行星轮系运动微分方程提供较为准确的啮合刚度。

关键词：变位齿轮；石川公式；外啮合刚度；内啮合刚度

齿轮传动因结构紧凑、效率高、能传递大的作用力等优点而成为机械传动中应用最广泛的一种传动形式。齿轮传动系统是一种弹性的机械系统，在动态激励作用下会产生动态响应。动态激励分为外部激励和内部激励两类，即使外部激励为0，齿轮系统也会因同时啮合齿对数和啮合接触点位置的改变，以及轮齿的误差等引起内部激励而产生振动[1]。通常啮合齿轮对的重合度不是整数，啮合过程中单双齿啮合交替出现，随时间做周期性变化，轮齿的综合啮合刚度也随之变化。啮合刚度随时间变化产生刚度激励，是产生齿轮啮合内部激励的主要原因。因此，为了研究齿轮内部激励对齿轮系统动态响应的影响，对整个齿轮啮合过程进行分析，计算得到啮合过程中啮合刚度的变化规律是很有必要的，这是齿轮故障诊断、系统动态特性分析以及寿命预测等研究的基础。

随着计算机的快速发展，采用有限元方法计算齿轮时变啮合刚度比较普遍。通过建立齿轮对三维接触有限元分析模型可得到啮合轮齿间的时变刚度曲线[2-3]。但建立有限元模型需要考虑的因素较多，模型比较复杂，而且计算不同齿轮的啮合刚度需要建立不同的有限元模型，效率比较低。而用数值计算方法求轮齿的啮合刚度则省去了建模的过程，在已有的数学模型的基础上，通过改变参数数值即可求解，计算速度快，效率高，精度也满足要求。数值求解方法主要有日本的石川公式法[4]和Weber能量法。Weber能量法在国外应用较多[5-6]，国内也有学者应用Weber能量法对齿轮变形量进行推导[7-8]，但石川公式因固定系数较少、计算过程简单、运算量小、适用范围更广而更多地被应用[9]。

目前，随着汽车工业快速发展，尤其是新能源汽车的发展，行星轮系因体积小、质量轻、传动比大等优点，越来越多地被应用在汽车自动变速器中。行星轮系在AT变速器中可与离合器、制动器搭配作为主变速构件，在CVT自动变速器中可作为副变速构件增大传动比范围，在新能源汽车上可使用ECVT自动变速器与电动机共同实现变速。行星轮系齿轮啮合与定轴轮系齿轮啮合不同，行星轮系中行星架带动行星轮公转使得行星轮与太阳轮、行星轮与内齿圈啮合线不断变化，外啮合与内啮合同时存在。在现有的文献中，利用有限元方法求解行星轮系时变啮合刚度的研究较多，而在利用数值计算方法求解行星轮系时变啮合刚度的文献中以标准行星轮与太阳轮外啮合刚度求法为主，基本上没考虑变位齿轮外啮合的情况，更没有考虑变位行星轮与内齿圈内啮合的啮合刚度。鉴于上述情况，本文对正变位行星轮与太阳轮外啮合进行分析，并在此基础上推导了正变位行星轮与内齿圈的内啮合刚度。

1石川公式

在齿轮啮合传动过程中，啮合齿对数与啮合接触点位置的变化会导致齿轮综合啮合刚度随时间周期性变化。轮齿间啮合作用可以简化为啮合线方向上的时变弹簧，某一接触点的啮合刚度即为此时的弹簧刚度。GB/T 3480—1997中提出了齿轮啮合刚度的计算方法，将齿轮啮合刚度定义为使一对或几对同时啮合轮齿在1 mm齿宽上产生1 μm变形量所需要的啮合线上的载荷力。齿轮啮合刚度的数学表达式为[11]

(1)

式中：Fn为啮合线法向载荷；b为轮齿的齿宽；δ为轮齿在啮合线方向上单位齿宽综合弹性变形量。

啮合刚度为轮齿的固有特性，与所受力的大小无关，通过齿轮啮合每一时刻单位力作用下轮齿的综合变形量即可求得此时刻的齿轮啮合刚度。本文采用石川公式法计算齿轮啮合线方向上轮齿啮合的综合弹性变形量，并在此基础上求轮齿啮合刚度。

1.1标准齿轮石川公式

石川公式作为一种常见的齿轮轮齿综合弹性变形的计算方法，将复杂的齿轮渐开线齿廓简化为由矩形与梯形组合而成的当量齿形结构，矩形底部所在的圆为齿轮的齿根圆，矩形与渐开线齿廓的交点为啮合齿轮对中主动轮啮合开始点、被动轮啮合结束点，该点在渐开线齿廓上所对应的圆称为有效齿根圆，简化后的外齿轮齿廓石川公式当量齿形如图1所示。

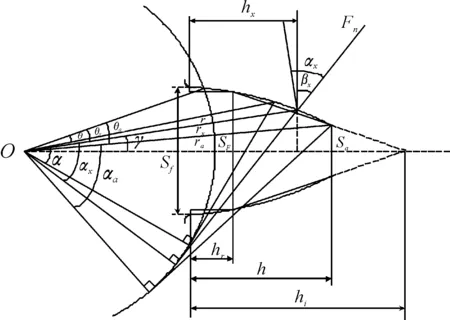
图1　外齿轮齿廓石川公式当量齿形

由图1中几何关系可得外齿轮齿廓石川公式当量齿形几何参数[12]。

1) 齿顶圆齿厚

(2)

式中：da为齿顶圆直径；r为分度圆半径；s为分度圆齿厚；α为渐开线齿廓分度圆压力角；αa为渐开线齿廓齿顶圆压力角。

2) 有效齿根圆齿厚

(3)

式中：dF为有效齿根圆直径；αF为渐开线齿廓有效齿根圆压力角。

3) 齿根圆齿厚

(4)

式中：df为齿根圆直径；αf为渐开线齿廓齿根圆压力角。

4) 矩形高

(5)

5) 齿形高

(6)

6) 啮合点所在齿轮圆半个齿厚角

(7)

式中αx为啮合点所在齿轮圆压力角。

7) 载荷作用角

(8)

8) 啮合点高

(9)

式中dx为啮合点所在齿轮圆直径。

9) 辅助尺寸

(10)

将轮齿简化之后，在求解齿轮啮合变形量之前进行一定的假设：

1) 在外啮合直齿圆柱齿轮传动中将齿轮轮体视为刚体，轮体部分变形为0；

2) 在内啮合直齿圆柱齿轮传动中内齿圈轮体为很薄的一部分，可近似忽略轮体变形的影响；

3) 忽略齿轮系统传动过程中的热变形。

此时，轮齿啮合综合弹性变形依赖于3部分的变形量：① 轮齿渐开线齿廓的弯曲变形δB(矩形部分的弯曲变形量δBr+梯形部分的弯曲变形量δBt)、啮合剪切变形量δs；② 轮齿齿根与轮体相连过渡曲线圆角部分的变形量δt；③ 由齿轮对啮合接触应力引起的局部变形量δc。

啮合齿轮对中单个轮齿变形量用数学公式表示为：

(11)

啮合齿轮对中1对轮齿的综合弹性变形量用数学公式表示为

(12)

式中：δp为主动轮轮齿啮合变形量；δg为从动轮轮齿啮合变形量；δc为轮齿接触应力引起的局部变形量。

根据简化图形的几何参数求解各个变形量的具体公式见文献[4]。

1.2变位齿轮石川公式

在齿轮传动系统中，为了改善标准齿轮的不足，突破标准齿轮的限制，通常对齿轮进行修正。现在最广泛应用的是通过改变刀具与齿轮轮坯的相对位置来切制齿轮，此时刀具的分度线与轮坯的分度圆不再相切，切制成的齿轮分度圆上齿厚s与齿槽宽e不再相等，这已不是标准齿轮，称其为变位齿轮。变位齿轮与标准齿轮相比，模数、分度圆压力角、分度圆直径、齿距并没有发生变化，发生变化的为分度圆齿厚、齿顶圆直径、齿根圆直径。

正变位外齿轮分度圆齿厚为

(13)

正变位内齿轮分度圆齿厚为

(14)

式中：m为模数；x为径向变位系数。

2行星轮系啮合刚度

2.1行星轮与太阳轮外啮合刚度

在角度变位齿轮传动中，正传动可以减小齿轮机构的尺寸，较大地提高齿轮机构的承载能力，在体积相对较小和承载能力高的行星轮系中应用较多。当行星轮与太阳轮均为正变位齿轮时，外啮合过程中分度圆与节圆不再重合，此时要保证齿轮传动时无侧隙正常啮合，其中一齿轮在节圆上的齿槽宽要等于另一齿轮在节圆上的齿厚，由此可得：

(15)

式中：α′为变位后的渐开线齿廓节圆压力角；xs为太阳轮变位系数；xp为行星轮变位系数。

正变位行星轮与正变位太阳轮外啮合齿轮传动的齿轮几何尺寸计算公式如表1所示。根据表1齿轮几何尺寸计算公式，可以得到按石川公式简化后的当量齿形参数中除啮合点高hx之外的其他参数。在外啮合过程中，齿轮副啮合点不断发生变化。当啮合点高hx随之发生变化，并且啮合点确定后可得到啮合点高hx，即可利用石川公式的当量齿形各部分变形量计算公式求解出啮合过程中综合弹性变形量，然后通过啮合刚度表达式得到在一个啮合周期内齿轮副啮合刚度随时间变化的曲线。啮合周期为

(16)

式中：nh为行星架转速；np为行星轮转速；zp为行星轮齿数。

表1　行星轮与太阳轮几何尺寸计算公式

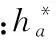
2.2行星轮与内齿轮内啮合刚度

内啮合是内齿轮与外齿轮进行啮合的传动，外齿轮是圆盘形的，外圈有齿,而内齿轮则是环形的，外圈光滑，轮齿分布在轮圈的内圆上，内齿轮齿廓如图2所示。

由图2内齿轮齿廓可知：内齿轮齿形与外齿轮齿形不同，内齿轮的轮齿与外齿轮齿槽部分相当，内齿轮的齿顶圆和齿根圆相当于外齿轮的齿根圆与齿顶圆。内齿轮轮齿简化为梯形与矩形组合成的石川公式当量齿形如图3所示。

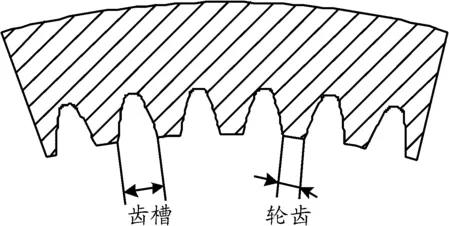
图2　内齿轮齿廓

图3　内齿轮轮齿石川公式的当量齿形

此时，内齿轮轮齿石川公式当量齿形中几何参数为:

齿顶圆齿厚

(17)

齿根圆齿厚

(18)

有效齿根圆齿厚

(19)

啮合点所在齿轮圆半个齿厚角

(20)

啮合点处法向载荷与轮齿中心线垂线的夹角

(21)

由于内齿轮的齿顶圆和齿根圆的位置刚好与外齿轮相反，因此简化后的内齿轮齿廓当量齿形中矩形高hr、齿形高h与啮合点高hx的计算公式与式(5)、(6)、(9)相差一个负号，而辅助尺寸hi的计算公式与式(10)相同。

对于正变位的行星轮与内齿圈内啮合，无侧隙正常啮合传动时啮合角计算公式为

(22)

实际中心距a′及中心距变动系数y计算公式与外啮合时相同，而齿顶高降低系数不同，其计算公式为

(23)

由于正变位行星轮与内齿圈内啮合传动时行星轮几何尺寸计算方法与外啮合时相同，因此仅列出内齿轮的几何尺寸计算公式如表2所示。

表2　内齿圈的几何尺寸计算公式

注：xr为内齿圈变位系数。

对行星轮与内齿圈内啮合过程进行分析，画出齿轮啮合过程简图，如图4所示。图4中：齿轮1为行星轮；齿轮2为内齿轮；N1N2为啮合过程的理论啮合线，在内啮合时其为两啮合齿轮基圆的外公切线。与外啮合时理论啮合线为两齿轮的内公切线所不同，在内啮合过程中，行星轮为主动轮，以行星轮有效齿根圆与内齿圈齿顶圆接触啮合点B2开始啮合，行星轮的凸齿面与内齿圈的凹齿面逐渐接触，以行星轮齿顶圆与内齿圈有效齿根圆接触啮合点B1结束啮合，B1B2为实际啮合线。与齿轮外啮合时实际啮合线在理论啮合线内不同，内啮合的实际啮合线在理论啮合线的延长线上。在实际啮合线B1B2中，B2C、B1D为双齿啮合区，CD为单齿啮合区。在单双齿啮合区内利用石川公式的当量齿形各部分变形量计算公式求得综合变形量，从而得到行星轮与内齿轮内啮合时一个啮合周期内的啮合刚度曲线，其啮合周期计算公式与式(16)相同。

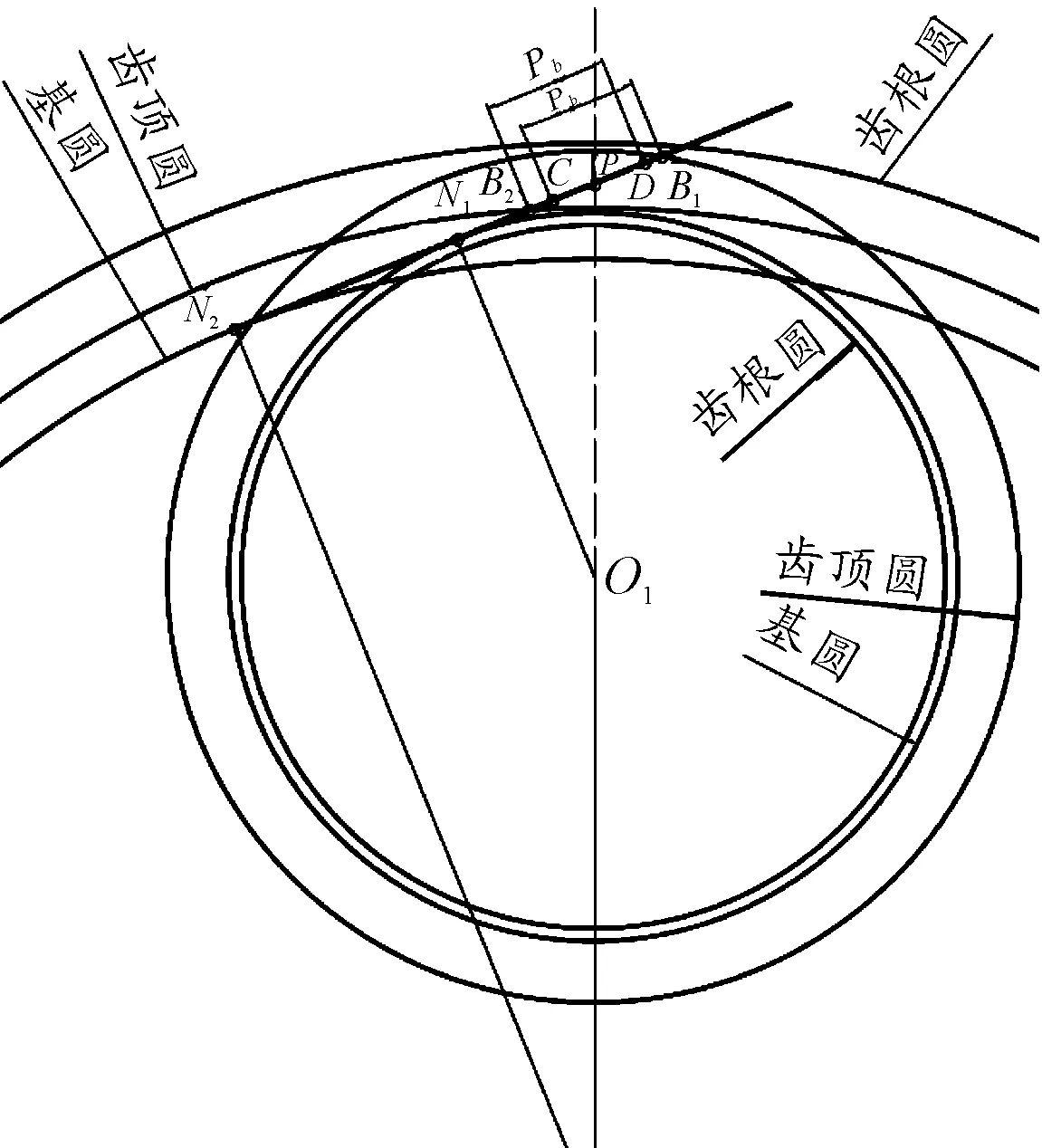
图4　行星轮与内齿轮内啮合过程简图

3算例与结果分析

3.1行星轮系啮合刚度

一个试制的等比例缩小风电行星齿轮箱正变位行星轮系各齿轮参数如表3所示。

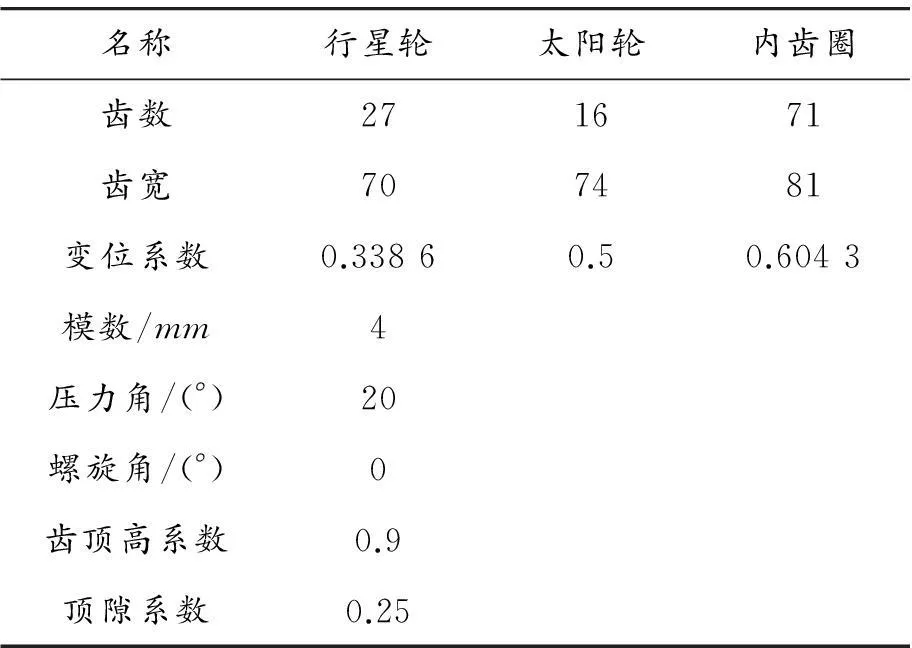
表3　行星轮系齿轮参数

用Matlab编程计算，设内齿圈固定，当输入轴行星架转速为600r/min时，计算得到行星轮相对行星架的转速为1 577.78r/min。行星轮与太阳轮外啮合刚度时频图如图5所示。外啮合的重合度为1.187 8，双齿啮合区占啮合周期比例为0.187 8。行星轮与内齿圈内啮合刚度时频图如图6所示。内啮合的重合度为1.527，双齿啮合区占啮合周期比例为0.527。

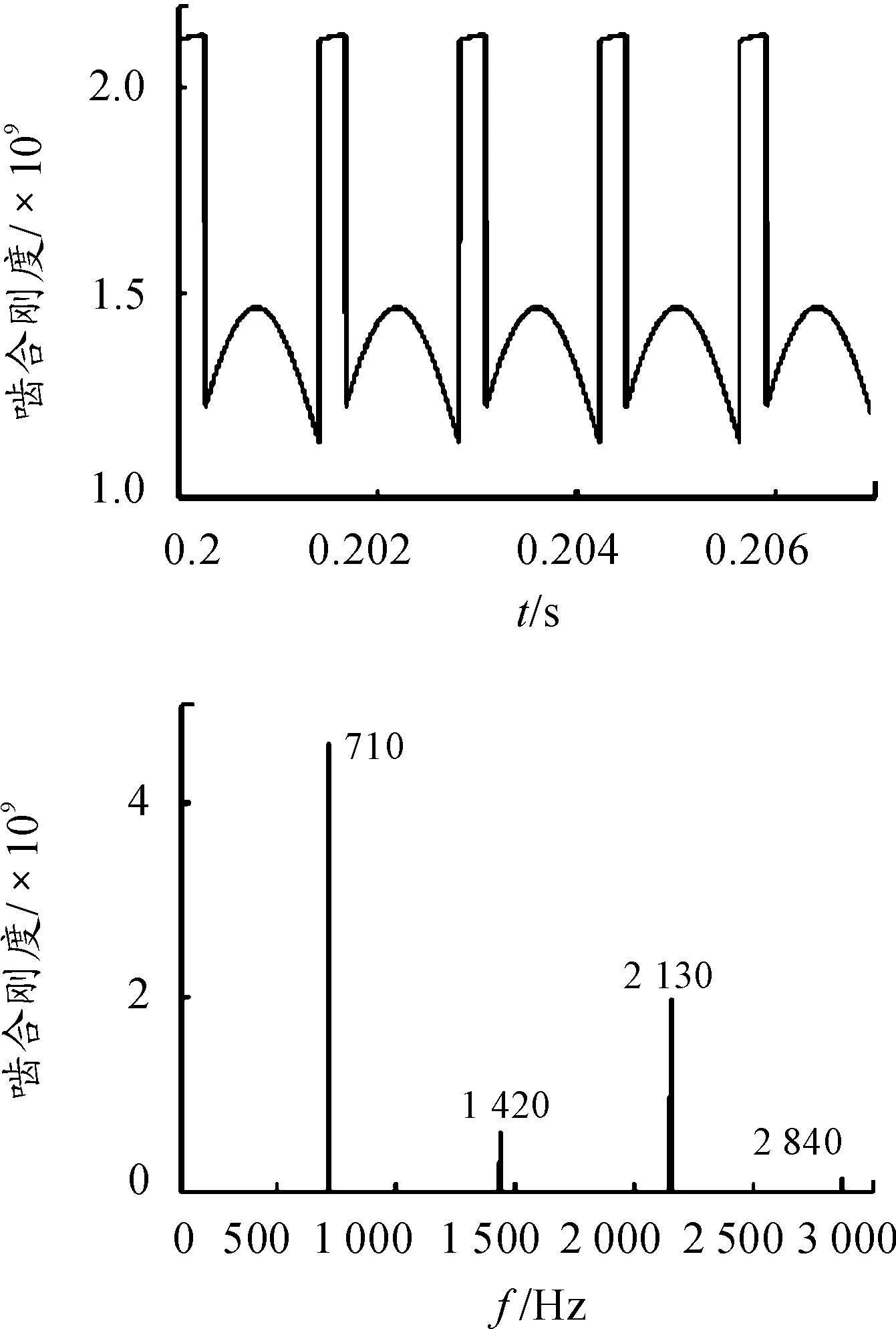
图5　外啮合刚度时频

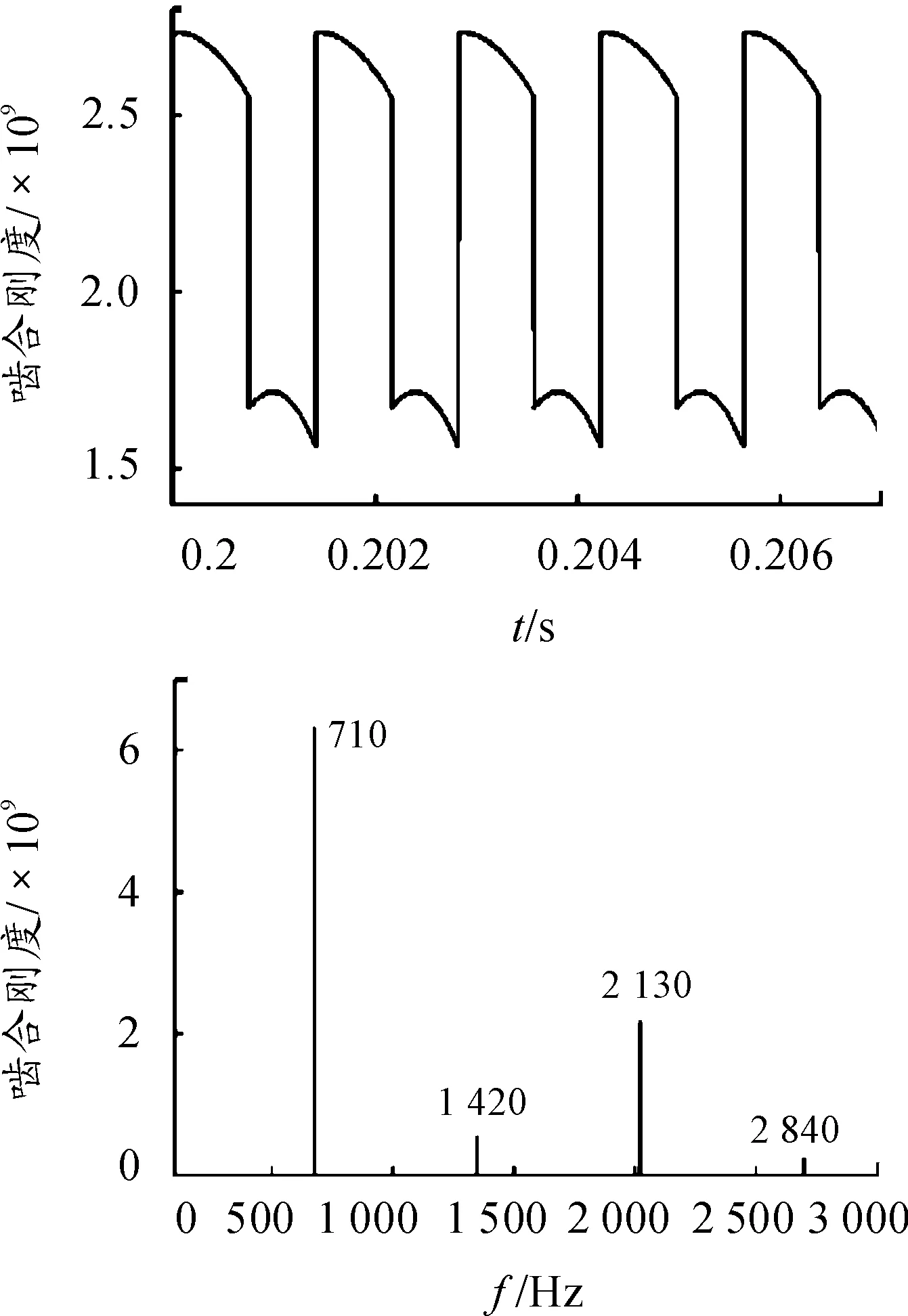
图6　内啮合刚度时频

3.2与Weber能量法计算结果对比

根据Weber能量法，通过Matlab编程得到齿轮啮合过程中时变啮合刚度。因Weber能量法未对轮齿进行简化，计算结果精度相对较高，ISO齿轮刚度计算标准也是以Weber能量法公式为基础的，故以Weber能量法计算结果为标准，对石川公式计算得到的静刚度和前4阶动刚度幅值进行比较，比较数据如表4和表5所示。

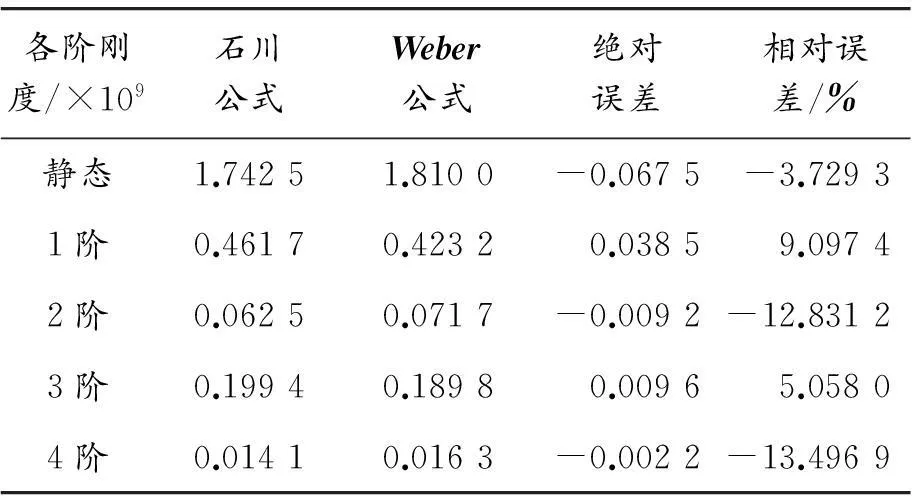
表4　行星轮与太阳轮外啮合刚度

注：数据四舍五入，取小数点后4位

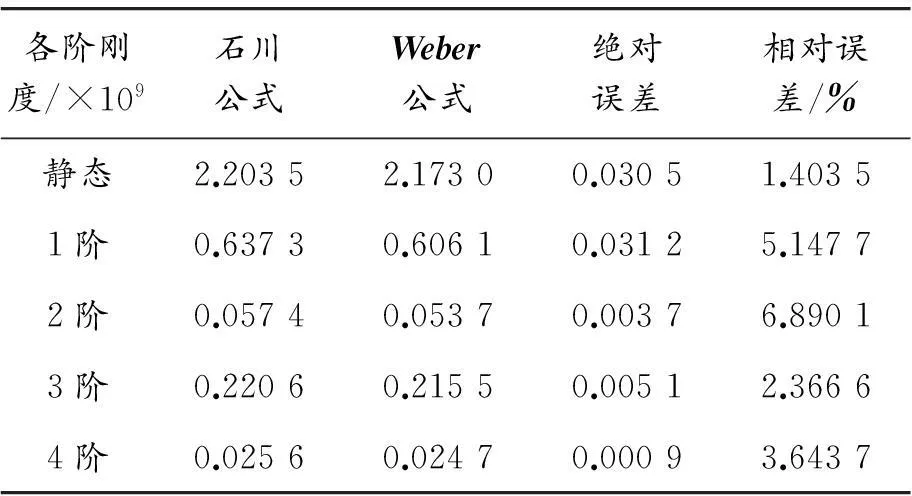
表5　行星轮与内齿圈内啮合刚度

注：数据四舍五入，取小数点后4位

数据分析结果表明：内啮合刚度相对误差整体要比外啮合要小，这是由于内啮合时内齿轮和外齿轮的当量齿形简化形成的误差相互补偿与抵消，石川公式计算结果更接近实际值。而无论内啮合与外啮合，其2、4阶啮合刚度幅值均比1、3阶啮合刚度幅值小一个数量级，相对误差要大些，但总体误差均在可以接受的范围内，可以验证上述分析中利用石川公式计算变位行星轮系啮合刚度的正确性与可行性。

4结束语

基于常见的外啮合轮齿石川公式当量齿形，详细推导了行星齿轮啮合的正变位外齿轮齿形几何参数的计算方法。根据内齿轮齿形与外齿轮齿形不同，做出内齿轮石川公式当量齿形，推导出正变位内齿轮齿形几何参数计算公式。利用石川公式计算方法，通过Matlab编程求解行星轮系内啮合与外啮合综合弹性变形量，得到行星轮系时变啮合刚度曲线，并将计算结果与Weber能量法计算结果进行对比分析。结果表明：静态刚度最大误差为3.7%，不考虑小幅值动态刚度时前4阶谐波幅值最大误差约为9.1%，能满足精度要求，验证了本文所提计算方法的正确性，可为行星轮系动力学特性分析提供较准确的啮合刚度，较有限元法更为有效和方便，计算效率更高。

参考文献：

[1]李润方，王建军.齿轮系统动力学—振动、冲击、噪声[M].北京：科学出版社,1997:11-12.

[2]LIR,YANGC,LINT,etal.Finiteelementsimulationofthedynamicalbehaviorofaspeed-increasegearbox[J].Journalofmaterialsprocessingtechnology,2004,150(1):170-174.

[3]DELRINCONAF,VIADEROF,IGLESIASM,etal.Amodelforthestudyofmeshingstiffnessinspurgeartransmissions[J].MechanismandMachineTheory,2013,61:30-58.

[4]日本机械学会.齿轮强度设计资料[M].李茹贞,赵清慧,译.北京：机械工业出版社,1984:28-35.

[5]TAVAKOLIMS,HOUSERDR.Optimumprofilemodificationsfortheminimizationofstatictransmissionerrorsofspurgears[J].JournalofMechanicalDesign,1986,108(1):86-94.

[6]YANGDCH,LinJY.Hertziandamping,toothfrictionandbendingelasticityingearimpactdynamics[J].JournalofMechanicalDesign,1987,109(2):189-196.

[7]杨长辉,徐涛金,许洪斌,等.基于Weber能量法的直齿轮时变啮合刚度数值计算[J].机械传动,2015,39(2):59-62.

[8]颜海燕,唐进元,宋红光.直齿轮轮齿变形计算的数值积分法[J].机械传动,2005,29(2):7-9.

[9]李亚鹏,孙伟,魏静,等.齿轮时变啮合刚度改进计算方法[J].机械传动,2010,34(5):22-26.

[10]陈再刚,邵毅敏.行星轮系齿轮啮合非线性激励建模和振动特征研究[J].机械工程学报,2015(7):23.

[11]GB/T3480—1997.渐开线圆柱齿轮承载能力计算方法[S].中国:国家技术监督局,1997.

[12]黄祝庆.基于多体动力学的齿轮副建模与实验研究[D].南京：南京航空航天大学,2013.

(责任编辑杨文青)

Numerical Calculation of Planetary Gear Train Involute ModifiedGear Time-Varying Meshing Stiffness

YUE Xi-zheng, DING Wen-si, DING Kang, ZENG Zhi-jie

(School of Mechanical and Automotive Engineering,South China University of Technology, Guangzhou 510641, China)

Abstract:The time-varying gear meshing stiffness is the main cause of gear vibration. To caculate the time-varying meshing stiffness has vital significance. Based on geometric parameters calculation method of external gear tooth profile in positive modified planetary gear train, according to the differences between external and internal gear tooth profiles, the geometric parameters calculation method of internal gear tooth profile was deduced in detail. Using Ishikawa tooth deformation calculation formula and stiffness calculation formula, positive modified planetary gear train internal and external time-varying meshing stiffness curves can be got by Matlab programming. Compared with the calculation result of Weber energy method, maximum static stiffness error is 3.7% and the first four order harmonic amplitude maximum error is 9.1% without considering the small amplitude value of the dynamic stiffness. Calculation accuracy meets the requirements. It can provide relatively accurate meshing stiffness for motion differential equation of the planetary gear train.

Key words:modified gear; Ishikawa formula; external meshing stiffness; internal meshing stiffness

收稿日期：2016-03-09

基金项目：国家自然科学基金资助项目(51475169)

作者简介：岳喜铮(1989—)，男，硕士研究生，主要从事行星轮系动力学特性分析研究； 通讯作者 丁问司(1968—)，男，教授，主要从事机械系统动力学研究。

doi:10.3969/j.issn.1674-8425(z).2016.06.007

中图分类号：TH132.425

文献标识码：A

文章编号：1674-8425(2016)06-0038-07

引用格式：岳喜铮，丁问司，丁康， 等.行星轮系渐开线变位齿轮时变啮合刚度数值计算[J].重庆理工大学学报(自然科学)，2016(6):38-44.

Citation format：YUE Xi-zheng, DING Wen-si, DING Kang, et al.Numerical Calculation of Planetary Gear Train Involute Modified Gear Time-Varying Meshing Stiffness[J].Journal of Chongqing University of Technology(Natural Science)，2016(6):38-44.