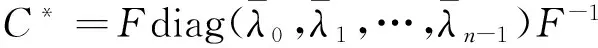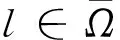循环矩阵填充的均值算法

余丽峰, 王川龙

(1.山西大学 数学科学学院，山西 太原　030006；2.太原师范学院 工程科学计算山西省高等学校重点实验室，山西 太原　030012)



循环矩阵填充的均值算法

余丽峰1, 王川龙2*

(1.山西大学 数学科学学院，山西 太原030006；2.太原师范学院 工程科学计算山西省高等学校重点实验室，山西 太原030012)

摘要：在奇异值阈值法的基础上，针对循环矩阵的特殊结构分别对一般低秩复循环矩阵和特殊低秩实循环矩阵作保结构的均值算法.首先给出构造低秩循环矩阵的方法；其次，给出了修正的保结构算法；最后通过数值实验验证结果.

关键词：循环矩阵；矩阵填充；算法；阈值

0引言

自从Candés和Recht在2009年提出通过凸优化进行矩阵填充[1]，矩阵填充就在信息领域快速发展，研究人员后续提出了很多理论[2-5]和算法[6-9].矩阵填充问题可以应用到很多领域，例如：控制[10]、计算机图像[3]和机器学习[11,12]等.循环矩阵在信息处理和图像处理上都有重要的应用.目前，还没有人研究循环矩阵的保结构算法，本文就将针对循环矩阵的特点对其进行研究.

对循环矩阵的填充问题可以表示为下面的凸优化问题

s.t.PΩ(X)=PΩ(M)

(1)

其中:X和M均是循环矩阵，Ω⊂{-n+1,…,-1,0,1,…,n-1} .

定义一个位移矩阵Rl：

(2)

l=0,…,n-1

一般而言，循环矩阵都是方阵，因此这里的n1,n2相等记为n.

1生成低秩循环矩阵

循环矩阵的特殊结构导致了循环矩阵几乎都是满秩的，对于矩阵填充问题，一般意义上针对的是低秩矩阵，所以生成一个低秩的循环矩阵就是首要解决的问题.

1.1特殊低秩循环矩阵

最容易构成的是一类由循环向量生成的循环矩阵，这类矩阵只要满足：用来生成循环向量的数组元素个数可以整除该向量的维数即可，这样生成的循环矩阵的秩即数组的个数.

其实，这是由一个秩较小的满秩循环矩阵构成的一个分块循环矩阵，该分块矩阵中只有这一个矩阵.

例设a=(1,2,3)，则由a构成的循环向量为c={1,2,3,1,2,3}，c的维数6可以整除a的维数3，因此由a,c构成的循环矩阵分别为

和

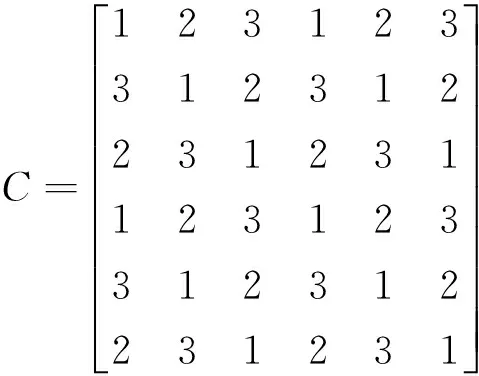
显然，

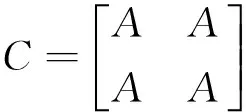
若c={1,2,3,1,2}，则可生成循环矩阵

显然，上述矩阵是满秩的.

对于采样数据结构有特殊循环矩阵定义那样的特点，可以按照分块矩阵做填充.稍后对其进行分析.下面描述生成普通低秩循环矩阵的方法.

1.2低秩循环矩阵

对于一个n×n的循环矩阵C有n个互不相同的特征值，文献[13]有：

F-1CF=diag(λ0,λ1,…,λn-1)

(3)

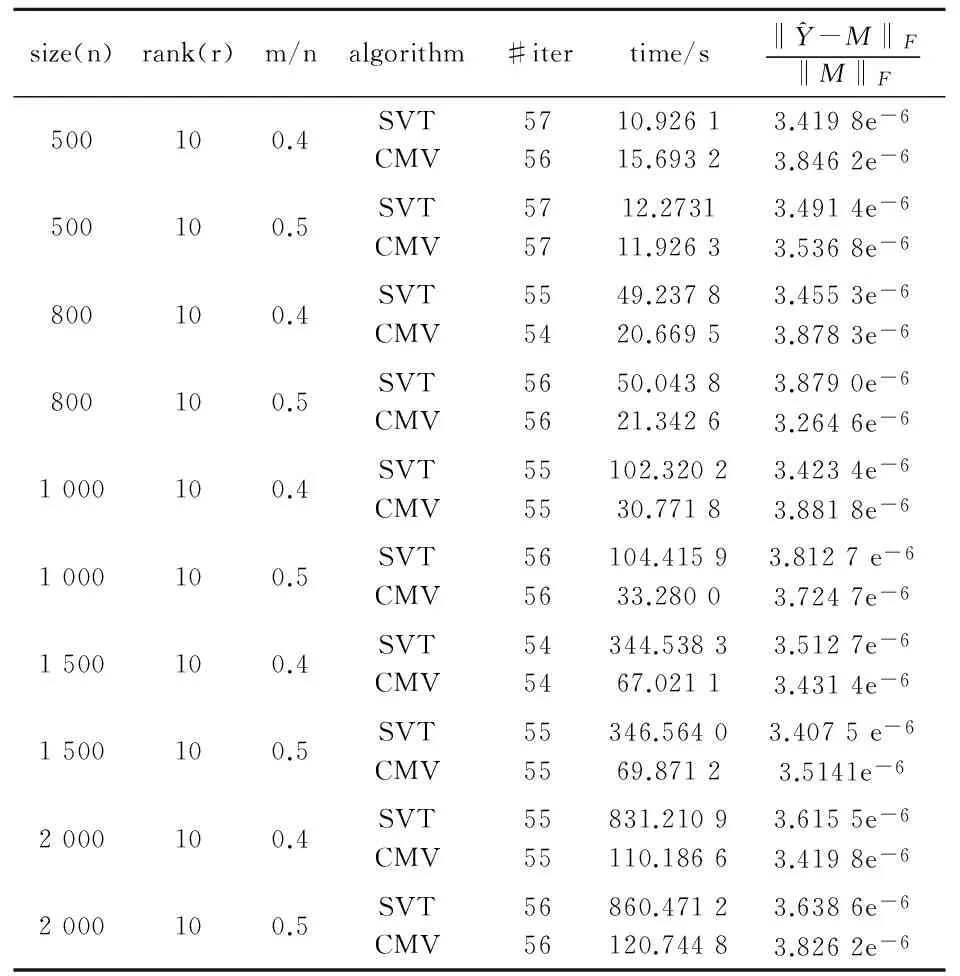
可知，假设给定一组向量λ1,λ2,…,λn-1，该向量有r(r

C=Fdiag(λ0,λ1,…,λn-1)F-1

(4)

如此就可得出一个低秩的循环矩阵C，记Λ=diag(λ0,λ1,…,λn-1).

由于F∈Cn×n，Λ=diag(λ1,λ2,…,λn-1) ，由Fourier矩阵的结构特点知，生成的低秩循环矩阵C∈Cn×n，是个复矩阵.如何利用循环复矩阵的特点，得到一个保持循环矩阵结构的算法，就是接下来要做的工作.

2算法

2.1低秩复循环矩阵填充

由(4)可知

C=Fdiag(λ0,λ1,…,λn-1)F-1，

则

运算如下：

C*=(Fdiag(λ0,λ1,…,λn-1)F-1)*=

(F-1)*(diag(λ0,λ1,…,λn-1))*F*=

则

CC*=Fdiag(|λ0|2,|λ1|2,…,|λn-1|2)F-1

由文献[14]可知，C的奇异值σi为|λi|,(i=1,…,n)对任意的C，F左奇异矩阵，F-1为右奇异矩阵，但直接利用傅里叶变换代替奇异值分解的算法并不收敛.

按照文献[15]的算法，类似的对循环矩阵的奇异值分解做一个均值算法来保持结构.

算法1循环矩阵填充的均值保结构算法(The Mean Algorithm for Circulate Matrix简称CMA算法)

初始化：Ω为下标集合，PΩ(M)为样本值，τ0为参数，c为常数且0

第一步：对矩阵Yk进行奇异值分解

[Uk,Σk,Vk]=svd(Yk)

令

Xk+1=UkDτk(Σk)Vk;

第二步：计算

cl=

Rl是(2)中的Rl且令

第三步：若‖Yk+1-Yk‖F/‖Yk‖F<ε，停止；否则，τk+1=cτk，k:=k+1；转第一步.

经过实验发现,均值算法对低秩循环复矩阵的填充效率并不理想，虽然结构可以保持，但运行时间过长，误差变化不大，因此可以判断出是求均值耗费的时间过长.因此这个算法还需在均值修正或奇异值分解上做改进.

2.2特殊循环实矩阵填充

算法2特殊循环矩阵的均值算法(The Mean Value Algorithm for Special Circulate Matrix简记为CMV)在CMA算法的基础上，用Lanczos 方法对Yk进行奇异值分解，只需将算法1的第一步更改为：

[Uk,Σk,Vk]=lansvd(Yk)

由此得到一个新的算法.

算法3特殊循环矩阵的降阶奇异值算法(The Reduce Order Singular Value Thresholding Algorithm for Special Matrix简记为RSVT) 改变算法的初始化采样矩阵，

初始化：记样本下标集合Ω，Ω∈{-m+1,…,-1,0,1,…,m-1}，m=n/2，m/r∈Z+，样本元素PΩ(M)，M是特殊循环矩阵C的m阶顺序主子矩阵，误差ε，参数τ，c为常数且0

第一步：对矩阵Yk进行奇异值分解

[Uk,Σk,Vk]=svd(Yk)

令

Xk+1=UkDτk(Σk)Vk;

第二步：计算

cl=

Rl是(2)中的Rl且令

第三步：若‖Yk+1-Yk‖F/‖Yk‖F<ε，停止；否则，τk+1=cτk，k:=k+1；转第一步.

由1.1的定义可知一类特殊的低秩循环矩阵，若存在一个秩为r的低阶循环矩阵A，一个所有元素均是1的矩阵B，则有低秩循环矩阵：

C=B⊗A

(5)

则C的秩为r.

由文献[16]可知Kronecker积关于范数和运算的几点性质，所以根据(5)式得

‖C‖F=‖A‖F‖B‖F

(6)

由于B是所有元素均为1的矩阵，所以对于m阶B就有

‖B‖F=m

(7)

可求得B的特征值λB等于奇异值σB等于m. 同样由文献[16]可知Kronecker 积有分配率，用式子可表示为：

C⊗A±C⊗B=C⊗(A±B)

(8)

利用式(6)，(7)和(8)可得如下简单定理:

(9)

由式(9)可以看出，对于此类循环矩阵，只需要对其r阶顺序主子矩阵(即循环矩阵的前r行r列)进行填充即可.由该类循环矩阵生成的方式可知，其r阶顺序主子矩阵是一个低阶满秩的矩阵，由此可知，要解决这个问题，就要解决低阶满秩填充的问题.

在解决填充问题之前，先发现了这类分块循环矩阵与决定其秩的小块循环矩阵的特征值和奇异值之间的关系，其关系见定理2.

定理2已知C=B⊗A，A是r阶的循环矩阵，B是元素均为1的m阶矩阵，若A的特征值为λ1,λ2,…,λr，则C的特征值为mλ1,mλ2,…,mλr.同理，若A的奇异值为σ1,σ2,…,σr，则C的奇异值为mσ1,mσ2,…,mσr.

证明：由循环矩阵的特点有

F-1CF=diag(ξ1,ξ2,…,ξr) ，

即

F-1(A⊗B)F=(F-1AF)⊗(F-1BF)=

diag(λ1,λ2,…,λr)⊗m

所以

ξi=mλi,(i=1,…,r),ξj=0,(j=r+1,…,n);

同理，得到奇异值为mσ1,mσ2,…,mσr.

因此，求得的局部误差就等于全局误差.

本文所有算法的收敛性分析均与文献[15]相同，文献[15]的全部引理定理仍然成立，具体引理定理及详细证明过程见文献[15].

3数值实验

表1　循环矩阵填充的SVT和CMV算法比较

表2　特殊循环矩阵填充的RSVT

由定理1可得到一个最简循环填充矩阵，但得到的矩阵是一个低阶满秩矩阵，经验证发现不能用已知的低秩矩阵填充方法求解，但这仍然提供了一种思路，RSVT算法就是在此基础上得到的.由表2可知，将特殊循环矩阵按规律降阶也能达到快速的效果，而且针对这类特殊矩阵，效果甚至略优于均值算法.因此，可以通过取顺序主子矩阵，顺序主子矩阵的阶数必须远大于秩.

4结论

本文针对低秩循环矩阵的复矩阵结构，运用其特殊性质，对低秩循环矩阵做一个保结构的算法.首先，给出求低秩循环矩阵的方法；其次，提出修正的保结构算法；最后通过数值实验观测分析.并对一类特殊结构的实循环矩阵进行填充，利用Kronecker积得到降阶算法.在数值实验中得出对于一般的低秩复循环矩阵保结构算法效果不理想，仍然可以进行改进，而对于特殊的实循环矩阵降阶算法还可以继续改进.

参考文献

[1] E.J.Candés,B.Recht. Exact matrix completionvia convex optimization[J].Foundations of Computational Mathematics,2009,9:717-772.

[2] E.J.Candés,T.Tao.The power of convex relaxation:Nearoptimal matrix completion[J].IEEE Transactions on Information Theory,2010,56:2 053-2 080.

[3] R.H.Keshavan,A.Montanari,S.Oh.Matrix completion from a few entries[J].IEEE Transactions on Information Theory,2010,56:2 980-2 998.

[4] B.Recht.A simpler approach to matrix completion[J].Journal of Machine Learning Research,2011,12:3 413-3 430.

[5] G.A.Watson.Characterization of the sub-diffe-rential of some matrix norms[J].Linear Algebra and Its Application,1992,170:33-45.

[6] Z.Lin,M.Chen,Y.Ma.The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[EB/OL].http://arxiv.org/abs/1009.5055,2010-09-26.

[7] J.F.Cai,E.J.Candés,Z.Shen.A singular value thresholding algorithm for matrix completion[J].SIAM Journal on Optimization,2010,20:1 956-1 982.

[8] D.Goldfarb,S.Ma.Convergence of fixed-point continuation algorithms for matrix rank minimization[J].Foundation of Computational Mathemtics,2010,11:183-210.

[9] B.Recht.A simpler approach to matrix completion[J].Journal of Machine Learning Research,2011,12:3 413-3 430.

[10] M.Mesbahi,G.P.Papavassilopoulos.On the rank minimization problem over a positive semi definite linear matrix inequality[J].IEEE Transactions on Automatic Control,1997,4:239-243.

[11] Y.Ami,M.Fink,N.Srebro,et al.Uncovering shared structures in multiclass classification[C]//Twenty-fourth International Conference on Machine Learning. New York:Association for Computing Machinery,ACM,2007:17-24.

[12] A.Argyriou,T.Evgeniou,M.Pontil.Multitask feature leafing[J].Advance in Neural Information Processing Systems,2007,19:41-48.

[13] 徐仲,张凯院,陆全.TOEPLITZ矩阵类的快速算法[M].西安:西北工业大学出版社,1998.

[14] G.H.Golub,C.F.Van Loan.Matrix computa-tions[M].3rd edition.Baltimore:The Johns Hopkins University Press,1996.

[15] Chuan Long Wang,Chao Li.A mean value algorithm for toeplitz matrix completion[J].Applied Mathematics Letters,2015,41:35-40.

[16] 王文丹，马昌凤.关于矩阵Kronecker积的几个范数公式[J].福建师范大学学报(自然科学版),2015,31(6):10-17.

【责任编辑：蒋亚儒】

A mean value algorithm for circulant matrix completion

YU Li-feng1，WANG Chuan-long2*

(1.School of Mathematical Science，Shanxi University，Taiyuan 030006，China；2.Higher Education Key Laboratory of Engineering Science Computing in Shanxi Province, Taiyuan Normal University, Taiyuan 030012, China)

Abstract:We propose a mean algorithm to preserving the structure according to the special structure of general low-rank complex circulant matrix and special low-rank real circulant matrix.Firstly,we construct a low-rank circulant matrix;Secondly,the preserving structure algorithm for the circulant matrix is proposed;Finally,the results are verified through numerical experiments.

Key words:circulate matrix; matrix completion; algorithm; threshold

*收稿日期:2016-06-11

基金项目：国家自然科学基金项目(11371275)

作者简介:余丽峰(1992-),女,山西忻州人,在读硕士研究生，研究方向：数值计算与优化 通讯作者:王川龙(1964-),男,山西侯马人，教授，博士，研究方向：数值计算与优化，clwang1964@163.com

文章编号：1000-5811(2016)04-0182-05

中图分类号：O241.6

文献标志码：A