基于对称多边形平滑磁链轨迹的直接转矩控制算法

范文进，　郑琼林，　杨中平，　林飞，　宋文胜，　Do Viet Dung

(1. 北京交通大学 电气工程学院，北京 100044；2. 西南交通大学 电气工程学院，四川 成都 610031；3.交通运输大学 机械系，越南 河内)



基于对称多边形平滑磁链轨迹的直接转矩控制算法

范文进1, 3，郑琼林1，杨中平1，林飞1，宋文胜2，Do Viet Dung3

(1. 北京交通大学 电气工程学院，北京 100044；2. 西南交通大学 电气工程学院，四川 成都 610031；3.交通运输大学 机械系，越南 河内)

摘要:以异步牵引电机为研究对象，提出了基于对称多边形磁链轨迹的直接转矩控制(direct torque control, DTC)算法。该算法通过分析励磁电流的变化，设计出一种具备圆形、六边形及两者之间多边形等多种对称磁链轨迹的控制算法，可获得更加平滑磁链轨迹，有利于提高谐波消除能力与开关频率的利用率。所提出DTC算法仅在传统DTC算法的基础结构上添加定子磁链调节算法，不需要复杂计算，因此具有结构简单与容易实现的优点。理论分析和实验结果证明了该控制算法的有效性和可行性。

关键词:异步牵引电机；直接转矩控制；对称多边形磁链；平滑轨迹

0引言

在传统直接转矩控制(direct torque control, DTC)算法中，逆变器的开关频率和开关次数与磁链调节器的容差呈反比关系，而定子电流谐波含量与磁链调节器的容差呈正比关系[1-3]。DTC理论被提出以后，根据磁链轨迹的不同，目前已经有基于圆形磁链轨迹[4]、三十边形磁链轨迹[5]、十八边形磁链轨迹[6]以及六边形磁链轨迹[7]4种传统DTC算法。其中，圆形磁链轨迹的磁链调节器容差最小，逆变器开关频率最高，谐波消除能力最好；而六边形磁链轨迹的磁链调节器容差最大，逆变器开关频率最低，谐波消除能力最差。

由于大功率牵引变流器开关频率较低[7-9]，因此采用DTC算法的异步牵引电机在恒转矩区必须采用不同磁链轨迹控制模式[10-11]。为了提高开关频率的利用率，改善定子电流的正弦度，文献[5,12]提出三十边形磁链轨迹DTC算法，将现有异步牵引电动机DTC全速度范围定子磁链轨迹扩展为圆形→三十边形→十八边形→六边形的多磁链轨迹控制模式；然而，在开关频率允许条件下，若增加更多对称多边形磁链轨迹以进一步减小定子电流谐波，采用该算法比较复杂。

文献[1]指出，基于圆形磁链轨迹DTC算法，通过调节磁链调节器的容差可获得多种多边形磁链轨迹。该算法通过采用多种非零电压矢量实现磁链偏差不变的目的，因此难以获得六边形、十八边形或三十边形以及更多对称多边形磁链轨迹的控制效果。

传统DTC存在转矩波动大，开关频率不固定等缺点[13-14]。一种比较有效的解决方案是采用空间矢量调制(space vector modulation, SVM)直接转矩控制(DTC-SVM)算法[15]。在近年来提出的改进传统DTC算法中，DTC-SVM算法得到进一步研究与采用[16-19]。文献[20]基于空间矢量调制技术，根据电力牵引交流传动系统的分段同步调制方案，介绍了三十边形、四十二边形、五十四边形等各种定子磁链轨迹的设计方法；但这种改进算法削弱了传统DTC结构简单的特性[21]，而在恒转矩范围内的中高速段的低开关频率场合，传统DTC算法具有更加优异的性能[12]。

针对上述问题，在开关频率允许的条件下，以提高谐波消除能力和开关频率的利用率以及鲁棒性与实现简单为目标，提出了更加平滑的对称多边形磁链轨迹DTC算法。将现有异步牵引电动机DTC全速度范围定子磁链轨迹扩展为：圆形→对称多边形…对称多边形→六边形的多磁链轨迹控制模式。本文首先分析了基于圆形，六边形，十八边形以及三十边形磁链轨迹的传统DTC算法；在此基础上提出了基于对称多边形磁链轨迹的DTC算法；最后，对所提出的DTC算法进行了实验验证。

1基于磁链轨迹的DTC算法

1.1基于圆形磁链轨迹的DTC算法

传统圆形磁链轨迹控制模式的基本思想是使磁链幅值在尽可能小的偏差范围内波动，正与负磁链偏差值相等。

在Takahashi和Noguchi提出的DTC系统中[4]，采用三点式转矩滞环控制器和两点式磁链滞环控制器，达到了使用多种电压矢量同时控制转矩与磁链的目的。该方法应用在低速域和小功率场合时有较好的控制性能。考虑到牵引逆变器的低开关频率要求，且在中高速域反向电压矢量会使转矩下降得较快，导致转矩波动较大。所以，采用两点式滞环控制器代替三点式转矩滞环控制器，可取消反向电压矢量。圆形磁链轨迹与空间电压矢量在d-q定子静止坐标系上的分布情况如图1所示，基于圆形磁链轨迹DTC系统结构框图如图2所示，电压矢量表以电机顺时针旋转来制定，如表1。

图1　圆形磁链轨迹与空间电压矢量Fig.1　Circular stator-flux locus and space voltage vector

1.2现有对称多边形磁链轨迹的DTC算法

1.2.1基于六边形磁链轨迹的DTC算法

六边形磁链轨迹控制模式的系统控制框图和定子磁链轨迹与三相静止坐标系dabc分别如图3和图4所示。

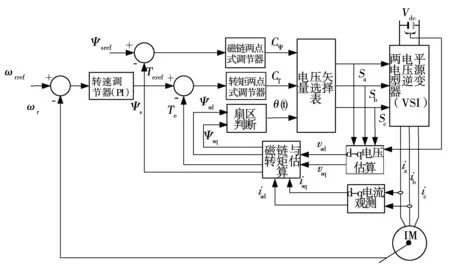
图2　圆形磁链轨迹DTC系统结构框图Fig.2　Block diagram of DTC system with circle　　　stator-flux locus

CTCYq(1)q(2)q(3)q(4)q(5)q(6)11V4(100)V6(110)V2(010)V3(011)V1(001)V5(101)0V6(110)V2(010)V3(011)V1(001)V5(101)V4(100)01V0(000)V1(111)V0(000)V1(111)V0(000)V1(111)0V1(111)V0(000)V1(111)V0(000)V1(111)V0(000)

图3　六边形磁链轨迹DTC系统结构框图Fig.3　Block diagram of DTC system with　　　hexagon stator-flux locus

控制系统中，磁链滞环控制器模块如图5所示，该模块由3个容差均为[-Ψsref,Ψsref]的滞环比较器构成，输入信号分别为三相静止坐标系dabc上的Ψda、Ψdb与Ψdc分量，输出信号为磁链开关状态，分别是S、S、S。

图4　六边形磁链轨迹与空间电压矢量Fig.4　Hexagon stator-flux locus and space　　　voltage vector

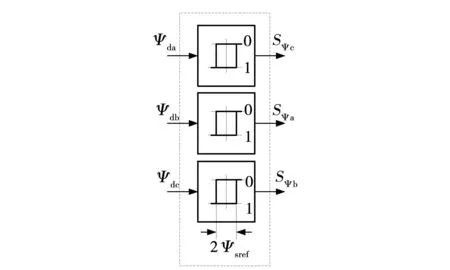
图5　磁链滞环控制器Fig.5　Flux hysteresis band controller

1.2.2基于十八与三十边形磁链轨迹的DTC算法

基于十八边形与三十边形磁链轨迹的DTC算法是在基于六边形磁链轨迹控制算法的基础上，在开关频率允许的条件下，为了进一步提高谐波消除能力而发展起来的一种改进控制算法。它的实现方法主要有两种：查表法和磁链滞环比较器法。

查表法是以实现圆形磁链轨迹的思想来制定电压开关表。若要实现十八边形磁链轨迹，则将原来六磁链扇区分为十八扇区，根据磁链当前所在扇区来选择适当的电压矢量以同时控制转矩与磁链。这种方法工作量大，多边形磁链轨迹的边数越多控制算法越复杂。具体方法可参考文献[12,20]。

磁链滞环比较器法是基于六边形磁链轨迹思想改进而成。首先将目标多边形磁链轨迹分为内与外六边形轨迹，然后通过已设计好的滞环比较器在内外六边形轨迹之间切换，最终实现对称多边形磁链轨迹。

十八与三十边形磁链轨迹DTC的系统控制框图[5,12]与六边形磁链轨迹控制模式系统控制框图基本相同，不同的是改变了磁链滞环控制器模块，即S模块，如图6所示。

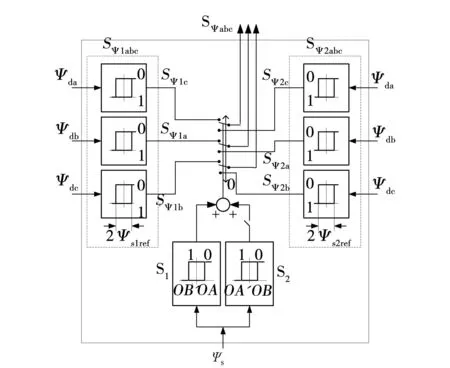
图6　十八与三十边形磁链轨迹的磁链滞环控制器Fig.6　Flux hysteresis band controller of stator-flux　　　locus for eighteen-corner and thirty-corner

该模块主要由两组实现不同尺寸六边形磁链轨迹磁链滞环控制器子模块S与S以及控制这两个磁链滞环控制器子模块交换工作的两个滞环比较器S1与S2所构成。以第1扇区为例，通过磁链滞环控制器模块实现上述两种磁链轨迹的原理图如图7所示。

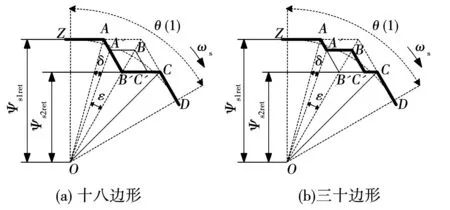
图7　十八与三十边形磁链轨迹的原理图Fig.7　Principle of stator-flux locus for eighteen-corner　　　 and thirty-corner

首先，当只有S、S和S1工作时，选择十八边形磁链轨迹工作模式，其在第1扇区内磁链运动轨迹为ZAB′CD，如图7(a)所示。其中S的容差设置为[-Ψs1ref,Ψs1ref]，S的容差设置为[-Ψs2ref,Ψs2ref]，其中Ψs2ref为

(1)

而S1的容差设置为[OB,OA]，OB和OA分别为：

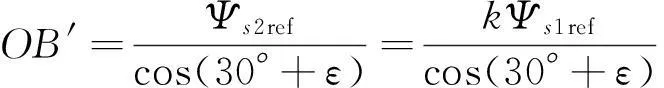
(2)

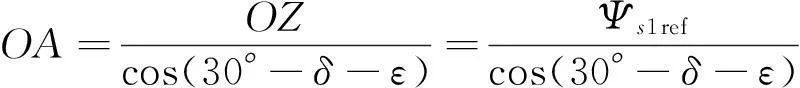
(3)

当磁链端点从Z向A运动时，S与S发出同样磁链开关状态，但由S1使S工作而S暂停工作。当磁链端点达到A点，即达到S与S1设置的上限容差，使其输出状态同时发生变化，S继续工作，磁链端点从A向B′运动。当磁链端点达到B′点，即因达到S1设置的下限容差使其输出状态发生变化，S1使S工作而S暂停工作，因为S开关状态未变，所以磁链端点从B′向C运动。当磁链端点达到C点，即达到S与S1设置的上限容差，使其输出状态同时发生变化，这时S与S发出同样磁链开关状态，但S1使S工作而S停止工作，因为S开关状态未变，所以磁链端点从C走向D。这样就形成了十八边形磁链轨迹。

(4)

(5)

综上所述，采用磁链滞环比较器法实现多边形磁链轨迹需要计算折角的角度，现有的方法是通过谐波分析来获得的。当多边形磁链轨迹的边数越多，需要计算折角的角度越多，需要求解非线性超越方程组越复杂[5,12]。

2对称多边形磁链轨迹的DTC算法

2.1对称多边形磁链轨迹的设计

传统六边形磁链轨迹直接转矩控制(direct self-control，DSC)算法中，六边形磁链虽然轨迹对称，但并非理想圆形，相应的定子电流(励磁电流)必然含有较大的谐波分量，畸变比较严重。由图7可得，为了改善六边形磁链顶角处的电流与磁链畸变，磁链滞环比较器法将顶角处变成单个或多个内折角。通常情况下，内折角数量越多，磁链轨迹越接近圆形，谐波消除能力越好。下面以电流波动平滑为目标，通过分析励磁电流来设计这一类的对称多边形磁链轨迹。

在异步电动机中，定子电流由产生转矩的有功电流分量和产生磁场的励磁电流分量组成，前者由负载与转矩控制算法决定，后者由磁链轨迹决定。因此，可通过分析励磁电流分量的性能指标来设计磁链轨迹。电机在空载稳态情况下运行时，转矩的电流分量可以忽略，所以定子电流只有励磁电流分量。这时定子磁链与定子电流同相，两者的关系如下所示：

(6)

其中:is为定子电流矢量;Ψs为定子磁链矢量；Lm为互感。

因为各个扇区磁链轨迹具有对称性，因此仅以三十边形磁链轨迹的第二扇区为例说明磁链轨迹设计对励磁电流的影响，如图8所示。

图8　第二扇区的三十边形磁链轨迹Fig.8　Thirty-corner stator-flux locus in the second sector

从式(6)可知，在该扇区，磁链的每一条边在定子励磁电流中表示出一个电流增加或减小过程，其中在A、C、E三点处是对应电流增加后的极值点，而在Z、B、D、F四点处是对应电流减小后的极值点。显然，若使定子励磁电流平滑变化，则A、C、E三点需要落在同一个圆形曲线上，而Z、B、D、F四点落在另一个圆形曲线上。这就是Takahashi和Noguchi[4]当初提出基于圆形磁链轨迹DTC算法的原有优点。因此，实现电流平滑变化需要满足以下两个等式：

(7)

这时定子励磁电流的波动范围为iA-iZ, 其中iA和iZ分别为：

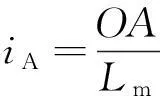
(8)

(9)

根据上面的分析，基于电流平滑变化的目标可设计出三十边形磁链轨迹在第二扇区对应轨迹的示意图如图9所示。

图9　三十边磁链轨迹的设计Fig.9　Design of thirty-corner stator-flux locus

图10　十八边磁链轨迹的设计Fig.10　Design of eighteen-corner stator-flux locus

随着电机速度的增加，开关频率也增加。当开关频率达到限定值，不再逐渐减小折角(图10中的虚线段轨迹)，可直接将十八边磁链轨迹转换至六边形磁链轨迹以满足开关频率要求。这是因为逐渐减小折角方法并没有改善电流波形，需要切换的电压矢量数量不变，因此开关频率也没有优势[3]。

2.2对称多边形磁链轨迹的实现方法

从上节对称多边形磁链轨迹的设计方案可看出，磁链轨迹具有不变的磁链偏差。理论上可以采用传统圆形磁链轨迹DTC算法[4]来实现。但该算法以多种电压矢量来控制磁链偏差不变为目标，在相邻扇区处容易出现附加边形，使得磁链轨迹对称性变差，附加增加开关频率。所以实际上难以获得六边形，十八边形或三十边形以及更多对称多边形磁链轨迹等这一类的控制效果。为了避免这个问题，下面给出解决方案。

从图9和图10可以看出，在第二扇区，折角分区内的部分磁链轨迹分别由V2与V6轮流切换作用来完成，而且该分区磁链偏差为固定的。扇区内剩下的两个分区部分磁链轨迹分别由V2与V6作用来实现。因此，可以通过结合圆形磁链轨迹与六边形磁链轨迹两种方法建立新的系统，实现本文提出的对称多边形磁链轨迹，即折角分区采用圆形磁链轨迹控制模式，其余两个分区采用六边形磁链轨迹控制模式。由此提出的对称多边形磁链轨迹DTC的系统控制框图如图11所示。

图11　提出对称多边形磁链轨迹DTC系统结构框图Fig.11　Block diagram of the proposed DTC system with　　　 the symmetrical polygon stator-flux locus

所提出控制算法的系统控制框图综合了圆形磁链轨迹DTC算法、六边形磁链轨迹DTC算法，增加了确定磁链轨迹变形数量的“σ给定”模块，以及“σ与当前磁链角度比较”模块，其作用是确定两者的切换时刻。

3实验结果

采用实验室的小功率异步电动机进行原理验证。具体电机参数为：额定电压VN=380 V，额定功率PN= 5.5 kW，额定转速ωN=1 450 r/min，定子电阻Rs=1.517，转子电阻Rr=1.483，定子漏电感Lls=2 mH，转子漏电感Llr=2 mH，互感Lm=172 mH，极对数np=2，转动惯量j=0.83 kg.m2。实验参数设定如表2所示。

表2　实验参数

为了验证磁链轨迹优化设计的控制算法的有效性，在同样的实验条件下通过改变磁链偏差对两种控制算法进行实验。下文中采用DTC1代表传统圆形磁链轨迹的DTC算法，DTC2代表本文提出的对称多边形磁链轨迹的DTC算法。

图12分别显示DTC1与DTC2在不同磁链偏差设置下对应的磁链轨迹实验结果。其中，左图为DTC1，右图为DTC2的结果。从图12的左图部分可以看出，当给定磁链偏差越大，磁链轨迹边形数目越少，最后可达到六边形磁链轨迹。但是这种轨迹只是近似的，因为在磁链轨迹中的两个相邻扇区处出现了附加边形(图中的标圆处)。显然这种方法只能实现近似的六边形，十八边形，三十边形等这一类的磁链轨迹，所以跟对应的对称多边形磁链轨迹相比对称性更差，实现时需要更大的逆变器开关频率与开关次数。

图12的右图部分可以看出，所提出的控制算法改善了传统圆形磁链轨迹控制模式的控制效果。在开关频率允许的条件下，只要适当地调节给定(即给定磁链偏差)就能实现六、十八、三十、四十二、五十四以及更多对称偏差不变的对称多边形磁链轨迹的目标。同现有的对称多边形磁链轨迹设计与实现方法相比较，若要获得更多边数的对称多边形磁链轨迹，显然这种方法更简单，更符合实际应用场合。

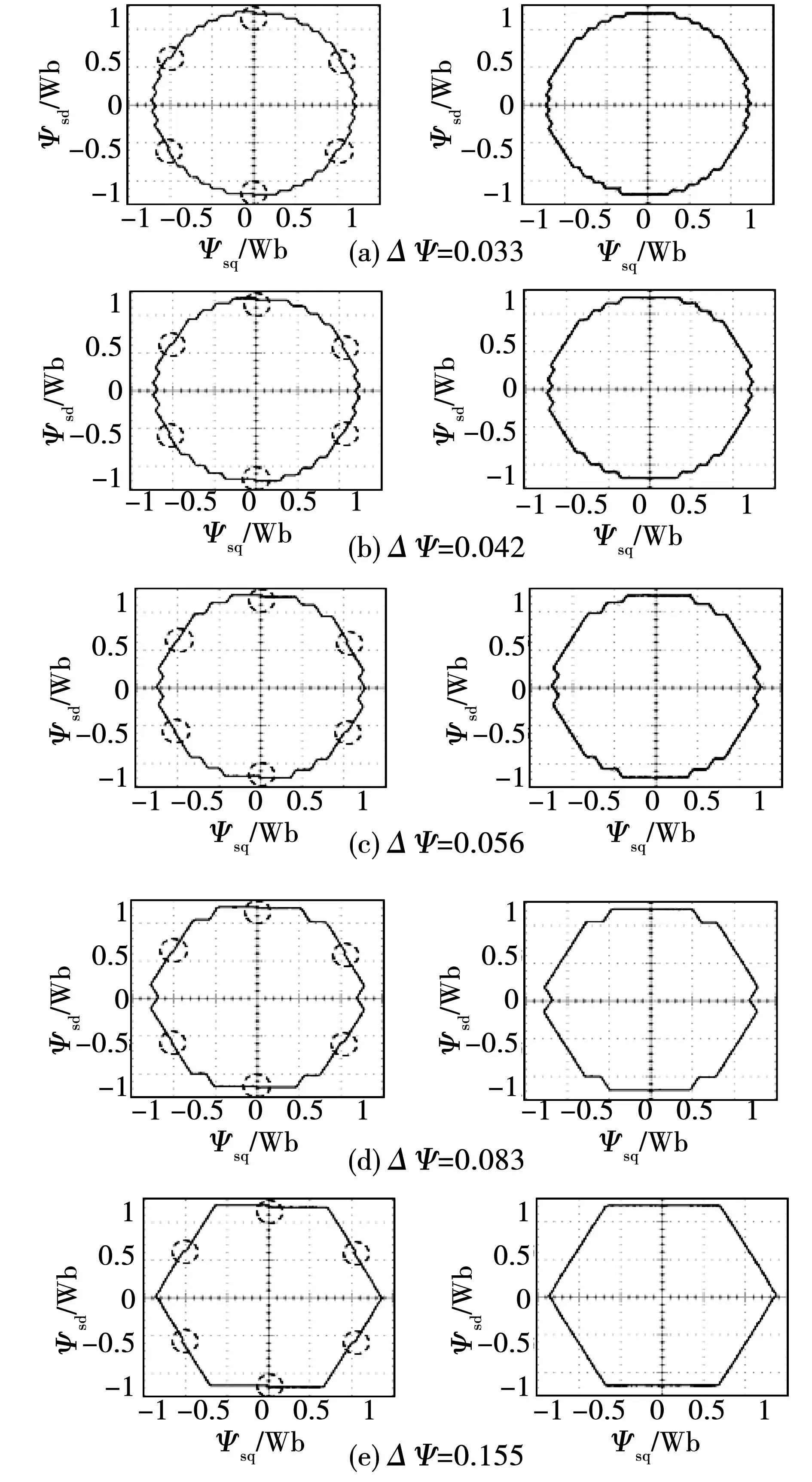
图12　DTC1与DTC2磁链轨迹的实验结果Fig.12　Experimental results of stator-flux locus　　　 with DTC1 and DTC2

4结论

本文以优化磁链轨迹与实现方法为研究目标，首先综合分析了各种基于磁链轨迹的传统DTC算法，然后在此基础上详细分析对称多边形磁链轨迹的控制算法原理，并提出实现方法。本文提出的对称多边形磁链轨迹的控制算法有如下的特点：

1)该算法是一种通过分析励磁电流的变化来设计出具备圆形、六边形以及圆形和六边形之间多种对称偏差不变的磁链轨迹的统一控制模型。在开关频率允许的情况下能实现更加平滑的对称多边形磁链轨迹(例如三十边形，四十二边形，五十四边形等)以提高谐波消除能力与开关频率的利用率。

2)该方法仅需在传统DTC结构中添加简单的磁链调节算法，实现时仅以磁链偏差和开关频率与谐波含量之间的关系为依据，直接调节磁链偏差，而不需要通过复杂的谐波分析与计算即可获得各种磁链轨迹。所以控制算法简单，容易实现。

最后通过小功率电机进行实验验证，实验结果表明了所提出的控制算法与传统圆形磁链轨迹DTC算法相比较有着更佳的控制性能，比现有的查表法和磁链滞环比较器法更加简单。

该算法不仅适合应用于采用多磁链轨迹控制模式的交流牵引传动系统，也适用于各种中、小功率的系统。

参 考 文 献:

[1]CASADEI D, GRANDID,SERRA G, et al. Effects of flux and torque hysteresis band amplitude in direct torque control of induction machines[C]//Industrial Electronics, Control and Instrumentation, Sep 5-9, 1994，In Pro. IEEE IECON'94, Bologna, 1994: 299-304.

[2]KAZMIERKOWSKI M B, KASPROWICZ A B. Improved direct torque and flux vector control of PWM inverter-fed induction motor drives[J]. IEEE Transactions on Industrial Electronics, 1995, 42(4):344-349.

[3]KANG J K, SUL S K. Analysis and prediction of inverter switching frequency in direct torque control of induction machine based on hysteresis bands and machine parameters[J]. IEEE Transactions on Industrial Electronics, 2001,48(3):545-553.

[4]TAKAHASHI I,NOGUCHI T. A new quick-response and high efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications, 1986, 22(5): 820-827.

[5]廖永衡，冯晓云，王珍. 低开关频率下基于直接自控制的谐波抑制方法[J]. 电工技术学报, 2012, 27(8): 126-132.

LIAO Yongheng, FENG Xiaoyun, WANG Zhen. Research on harmonic elimination in low switching frequency based on direct self control [J]. Transactions of China Electrotechnical Society, 2012, 27(8): 126-132.

[6]STEIMEL A. Further development of direct self control for application in electric traction[C]// Proceedings of the IEEE International Symposium on Industrial Electronics, Warsaw, Poland, 1996: 180-185.

[7]DEPENBROCK M. Direct-self control (DSC) of inverter fed induction machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4): 420-429.

[8]BAADER U, DEPENBROCK M, GIERSE G. Direct Self Control (DSC) of inverter fed induction machine: A basis for speed control without speed measuremen[J]. IEEE Transactions on Industrial Applications,1992,28(3): 581-588.

[9]周明磊，游小杰，王琛琛. 电力机车牵引传动系统矢量控制[J]. 电工技术学报, 2011, 26(9): 110-115，129.

ZHOU Minglei, YOU Xiaojie, WANG Chenchen. Vector control of driving system of locomotive[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 110-115，129.

[10]冯晓云. 电力牵引交流传动及其控制系统[M]. 北京: 高等教育出版社, 2009: 189-210.

[11]STEIMEL A. Direct self control and synchronous pulse techniques for high-power traction inverters in comparison[J]. IEEE Transactions on Industrial Electronics, 2004, 51(4): 810-820.

[12]廖永衡. 电力牵引传动系统直接转矩控制若干关键问题研究[D].成都: 西南交通大学, 2013.

[13]杨影，陈鑫，涂小卫，等. 占空比调制的永磁同步电机直接转矩控制[J].电机与控制学报,2014,18(4): 66-71.

YANG Ying, CHEN Xin, TU Xiaowei, et al. Direct torque control of permanent magnet synchronous motor based on duty ratio control[J]. Electric Machines and Control, 2014,18(4): 66-71.

[14]牛峰，李奎，王尧. 永磁同步电机模型预测直接转矩控制[J]. 电机与控制学报, 2015, 19(2): 60-67.

NIU Feng，LI Kui，WANG Yao. Model predictive direct torque control for permanent magnet synchronous machines[J]. Electric Machines and Control, 2015, 19(2): 60-67.

[15]HABLETER T G, PROFUMO F，PASTORELLI M M，et al．Direct torque control of induction machines using space vector modulation[J]. IEEE Transactions on Industry Applications, 1992, 28(5): 1045-1053．

[16]张华强，王新生，魏鹏飞,等. 基于空间矢量调制的直接转矩控制算法研究[J].电机与控制学报,2012,16(6): 14-18.

ZHANG Huaqiang, WANG Xinsheng, WEI Pengfei, et al. Study on direct torque control algorithm based on space vector modulation[J]. Electric Machines and Control, 2012,16(6): 14-18.

[17]王斌，王跃，王兆安. 无速度传感器的永磁同步电机无差拍直接转矩控制方法[J].电机与控制学报,2014,18(6): 42-49.

WANG Bin, WANG Yue, WANG Zhaoan. Deadbeat direct torque control of permanent magnet synchronous motor without speed sensor[J]. Electric Machines and Control, 2014,18(6): 42-49.

[18]林斌，孙丹，贺益康.永磁同步电机直接转矩控制高速运行范围拓宽[J].电机与控制学报,2014,18(9): 9-16.

LIN Bin, SUN Dan, HE Yikang. High-speed operation range extension for direct torque controlledpermanent magnet synchronous motors[J]. Electric Machines and Control, 2014,18(9): 9-16.

[19]孙丹，林斌，陈敏,等. HEV用开绕组永磁同步电机双逆变器协同控制[J]. 电机与控制学报, 2016, 20(2): 29-35.

SUN Dan, LIN Bin, CHEN Min, et al. Coordinate control of dual-inverter driven open-winding PMSM for hybrid electric vehicles[J]. Electric Machines and Control, 2016, 20(2): 29-35.

[20]宋文胜，冯晓云. 电力牵引交流传动控制与调制技术[M]. 北京: 科学出版社, 2014：11-14.

[21]牛峰，李奎，王尧.基于占空比调制的永磁同步电机直接转矩控制[J]. 电工技术学报, 2014, 29(11): 20-29.

NIU Feng, LI Kui, WANG Yao. Model predictive direct torque control for permanent magnetsynchronous machines based on duty ratio modulation[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 20-29.

(编辑：张楠)

Direct torque control algorithm based on smooth of symmetrical polygon stator-flux locus

PHAM Van-tien1, 3，Trillion Q. ZHENG1，YANG Zhong-ping1，LIN Fei1，SONG Wen-sheng2，DO Viet-dung3

(1.School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044, China;2.School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. Department of Mechanical Engineering, University of Transport and Communications, Hanoi, Viet Nam)

Abstract:A direct torque control (DTC) algorithm based on symmetrical polygon stator-flux locus was proposed with asynchronous traction motors as the research object. By analyzing the excitation current changes, a control algorithm characterized by multiple symmetrical stator-flux trajectories in shape of circle, hexagon or other polygons between them was designed. Smoother stator-flux trajectories were obtained and are favorable to improve the harmonic elimination capability and the switching frequency utility. This DTC algorithm is simple in structure and is easy to implement as it only requires adding stator flux regulation to the traditional DTC algorithms. Its effectiveness and feasibility are demonstrated by both theoretical analysis and experimental results.

Keywords:asynchronous traction motor; direct torque control; symmetrical polygon stator-flux; smooth locus

收稿日期:2015-05-27

基金项目：中央高校基本科研业务费专项资金(2014RC013)

作者简介：范文进(1981—)，男，博士，研究方向为轨道交通电力牵引传动技术；

通信作者:范文进

DOI:10.15938/j.emc.2016.07.005

中图分类号:TM 343

文献标志码:A

文章编号:1007-449X(2016)07-0032-08

郑琼林(1964—)，男，教授，博士生导师，研究方向为轨道交通牵引供电与交流传动，高性能低损耗电力电子系统，光伏发电并网与控制，电力有源滤波与电能质量；

杨中平(1971—)，男，教授，博士生导师，研究方向为轨道交通电力牵引传动技术、节能技术、高速列车系统优化设计技术；

林飞(1975—)，男，副教授，博士生导师，研究方向为电力电子与电力传动；

宋文胜 (1985—)，男，博士，研究方向为电力牵引交流传动控制；

Do Viet Dung(1955—)，男，副教授，博士生导师，研究方向为机车电传动。