三电机卷绕系统的状态反馈鲁棒控制
——LMI方法
2016-07-14侯海良年晓红彭智王忠
侯海良, 年晓红, 彭智, 王忠
(1.中南大学 信息科学与工程学院,湖南 长沙 410004; 2.湖南人文科技学院 信息学院,湖南 娄底 417000)
三电机卷绕系统的状态反馈鲁棒控制
——LMI方法
侯海良1,2,年晓红1,彭智1,王忠1
(1.中南大学 信息科学与工程学院,湖南 长沙 410004; 2.湖南人文科技学院 信息学院,湖南 娄底 417000)
摘要:针对具有强耦合、不确定性和非线性的三电机卷绕系统,提出一种基于线性矩阵不等式(linear matrix inequality,LMI)的全局鲁棒控制方法。首先,在三电机卷绕系统的数学模型的基础上给出了一种系统的稳态控制输入和参考速度的计算方法,得到了系统的动态误差模型。接着,考虑到卷绕过程中存在的参数不确定和时变性,引入区间矩阵进行描述,在此基础上,根据Lyapunov稳定性理论得到了使闭环系统鲁棒渐近稳定的LMI充分条件。最后,以实验室搭建的三电机卷绕系统为例进行了仿真和平台实验,实验结果证明了所提出的控制方法的有效性和鲁棒性。
关键词:卷绕系统;线性矩阵不等式;状态反馈;区间变量;鲁棒渐近稳定
0引言
多电机卷绕系统在造纸、印刷、纺织、金属箔、聚合物等生产工业中得到广泛应用。该类系统的主要目标是在控制张力稳定的基础上尽可能的提高处理速度,以实现在保证产品质量的基础上提高生产效率[1]。实际上,由于卷绕系统的工料张力和速度之间存在耦合,速度的变化会影响张力的变化,张力的变化也会引起速度的变化,这给实际控制带来了困难。目前,实际工业中的卷绕系统大多采用分散PI或者PID控制,将张力速度控制解耦成速度控制环和张力控制环,但对于一些控制精度要求较高的场合,这种类型的控制策略难以获得令人满意的控制效果[1-3]。文献[4]提出了一种针对钢管柔性生产线的开卷张力进行控制的二维模糊控制控制方案。文献[5]设计了模糊二阶自抗扰控制器实现了电机间张力和速度的解耦;文献[6-7]提出了基于极点配置的解耦控制方法,并分别应用到带钢平整机和退火机的张力速度控制中;文献[8-9]分别设计了带增益调度的二自由度H2和H鲁棒控制器,通过前馈单元实现张力和速度的解耦,通过反馈单元提高系统的抗干扰能力。然而,由于卷绕系统中存在时变和不确定参数,导致前述的解耦控制方法很难完全有效的抑制速度和张力之间的相互影响[10]。
在整个工作过程中,收、放卷辊的半径和转动惯量随时间大范围内变化,环境温度和湿度对工料杨氏模量和摩擦系数影响较大,因此,鲁棒性是卷绕系统控制器设计需要考虑的问题。文献[2]通过引入线性变参数策略(linear parameter varying,LPV)增强了PI控制器对半径变化的鲁棒性;文献[1,8-9,11]的控制器设计是基于卷绕系统的局部线性化模型,通过引入LPV[1,8]或者增益调度策略[1,8-9,11]增强控制器对半径和转动惯量变化的鲁棒性。文献[10]考虑了杨氏模量、辊子半径和转动惯量等参数有界不确定(偏离标称值±10%)情况下H控制器的设计问题。文献[12-13]利用神经网络、模糊控制的非线性逼近能力处理系统模型的不确定性。文献[14-15]分别提出了非线性滑膜控制和模型参考自适应控制,这两种控制方法都将卷绕系统的时变参数(如辊子半径、转动惯量等)融入到控制器中。实际上,在卷绕过程中,收、放卷辊的半径和卷动惯量是不断变化的,环境温度和湿度对工料杨氏模量和摩擦系数影响较大,有时根据生产的要求需要调整张力和速度的大小,因此,这些参数的值是不确定的或时变的。但由于实际条件的限制,半径和转动惯量只能在一定的范围内变化,环境温度和湿度对参数的影响也是有限的,参考张力和速度也只能在一定范围内重新设定。因此,这些参数可以看成区间变量[16],卷绕系统可以看成区间系统[17]。
本文研究了多电机卷绕系统的鲁棒镇定问题,提出了一种基于线性矩阵不等式(linear matrix inequality,LMI)的状态反馈鲁棒控制器的设计方法。首先在文献[14]的非线性数学模型基础上,采用Taylor公式得到了系统处于平衡状态时的控制输入并推导出动态误差模型。接着,为了处理动态误差模型中的不确定和时变参数,引入区间矩阵[17]进行描述。在此基础上,设计了基于状态反馈的鲁棒控制器,根据Lyapunov稳定性理论推导出使系统鲁棒渐近镇定的LMI充分条件。最后通过仿真和实验平台实验证明了本文方法的有效性。
1卷绕系统动态模型与预备知识
实验室研制的三电机卷绕系统实验平台如图1所示,该系统由放卷辊、牵引辊和收卷辊3个独立的机电子系统组成,3个子系统通过工料(白色牛皮纸带)联成一体。正常工作时,工料从放卷辊展开,经过一系列处理后由收卷辊收取。

图1 实验平台Fig.1 Experimental setup
图2为平台的结构示意图。图中Ri为第i个辊子的实时半径;vi为第i个辊子上工料的线速度,工料在辊子上无滑动时,工料线速度等于辊子线速度;系统的输入是电机的输出转矩ui(i=0,1,2);被控量为放卷张力t1、收卷张力t2和牵引辊速度v1,整个系统的速度由v1决定,放卷张力t1和收卷张力t2分别通过控制放卷和收卷电机的速度进行调节。

图2 实验平台示意图Fig.2 Sketch of the experimental setup
三电机卷绕系统的非线性动态数学模型为[14]:
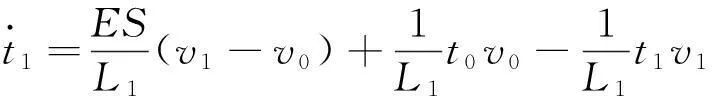
(1)

(2)

(3)

(4)
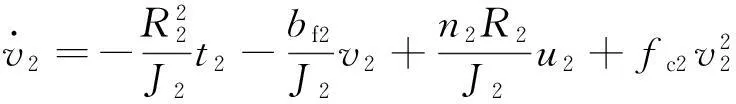
(5)

(6)
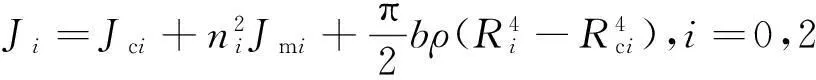
(7)

(8)
式中:Ji和bfi分别为第i个辊子的实时转动惯量和摩擦系数;ni为第i个电机轴与对应的驱动辊之间的传动比;E、S、ρ、b和h分别为工料的杨氏模量、截面积、密度、宽度和厚度;L1和L2分别为放卷辊到牵引辊和牵引辊到收卷辊的工料长度;t0为放卷前放卷工料的内张力;Jci和Rci分别为空收、放卷辊的转动惯量和半径;Jmi为电机侧旋转单元的转动惯量。其中放卷端的转动惯量J0和半径R0随着工料的释放而不断减小,由于收集处理后的工料而使收卷端转动惯量J2和半径R2不断增大。
在本节结束前给出一些后面证明中需要用到的定义和引理。

引理1[18]区间矩阵A∈[Am,AM],A可以写成
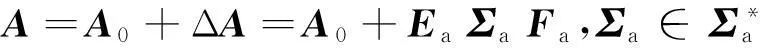
其中
A0=(Am+AM)/2,
ΔA=ΕaΣaFa,
HA=(AM-Am)/2=[ζij]n×n,



|χij|1,1i,jn}。
这里ei(i=1,2,…,n)为n×n维单位矩阵的第i个列向量。显然对∀Σ∈Σ*,有ΣTΣI。
引理2[19]设X和Y为合适维数的实矩阵,对于任意给定的正常数ε,有下列不等式成立:
XTY+YTXε-1XTX+εYTY。

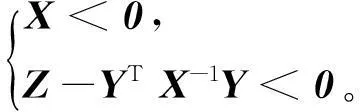
注:文中矩阵小于0表示该矩阵是负定的。本文中所有对矩阵大于0或小于0的描述都分别表示该矩阵是正定或负定的。
2鲁棒控制器设计
卷绕系统的控制输入分成两部分,一部分是稳态控制量,指在不考虑外界干扰和系统不确定性的情况下,保持张力和速度稳定在参考值时所需要的控制量;另一部分是控制补偿,当系统存在干扰作用时,使张力和速度跟随误差收敛所需要的控制量。
2.1稳态控制输入和误差动态模型
为了获得系统的稳态控制输入,定义如下变量:
(9)
式中,vri和tri为速度和张力的参考值,usi为稳定状态时的控制输入,Vi和Ti为速度和张力的跟踪误差,Ui为控制补偿。
采用Taylor公式将式(1)展开,忽略余项,同时将ti=Ti+tri代入有

(10)

(11)
放卷张力的跟随误差模型可表示为
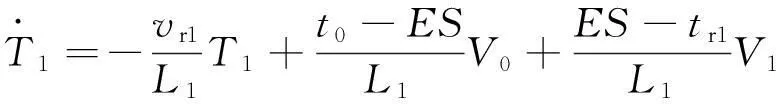
(12)
同样,采用Taylor公式可将式(2)展开为

(13)

(14)
放卷辊速度的跟随误差模型为

(15)
同样,由式(3)、式(4)和式(5)可以得到:
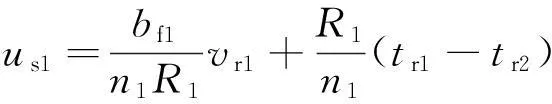
(16)

(17)
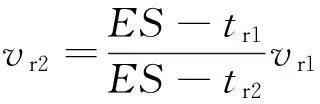
(18)
(19)

(20)
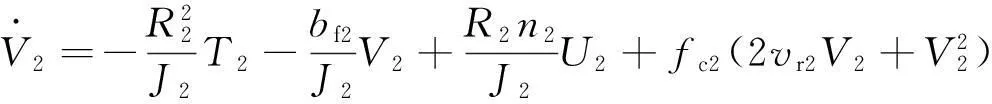
(21)
式(11)和式(18)为收、放卷辊的参考速度,对于任意一组设定值(tr1,tr2,vr1) ,其值是确定的。式(14)、式(16)和式(20)为系统稳定时的控制输入,它们是辊子半径、参考速度和参考张力的函数,因此,稳态控制输入对不同的工作点具有自适应能力。
根据式(12)、式(15)、式(17)、式(19)和式(21)可将系统误差模型写成

(22)
式中:
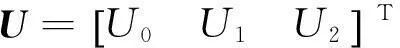
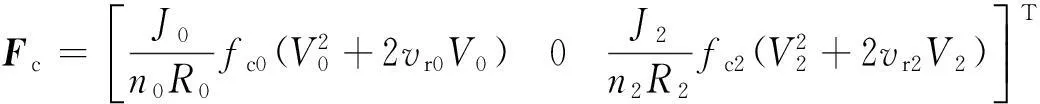
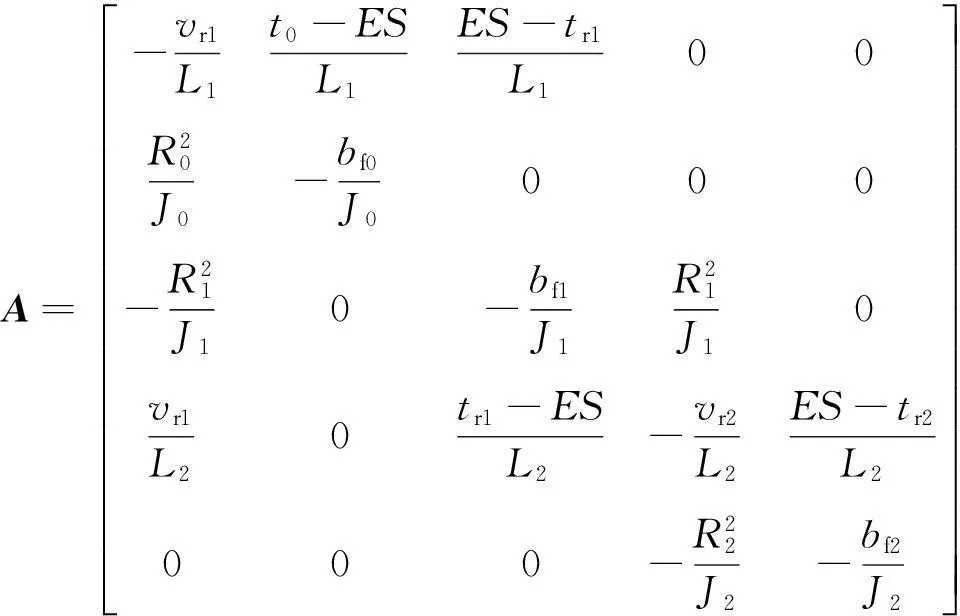
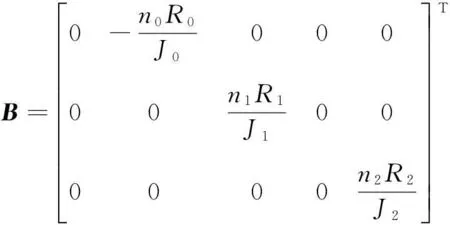
2.2状态反馈控制器设计
根据前面的分析可知,模型(22)中含有时变和不确定参数,要获得好的控制效果,设计的控制器必须有足够强的鲁棒性以消除这些参数的影响。下面将给出鲁棒控制器的设计过程。
对于给定的多电机卷绕系统,受实际工作条件的限制,其参数R0、R2、J0和J2在一定的范围内变化,设定值vr1、tr1和tr2也不能超过某一特定的值,环境对E和bfi(i=0,1,2)的影响也是有限的。因此,这些参数可以看成区间变量,下列假设是合理的。
(23)
根据区间变量的四则运算和代数性质[16],由式(7)可以求出在条件(23)下转动惯量J0、J2变化的上下界,收、放卷的参考速度vr0和vr2的上、下界也可由式(11)和式(18)得到。由式(22)可以看出系统矩阵A和输入矩阵B中的一些元素为上述区间变量的函数,根据区间变量的四则运算和代数性质[16]同样可以推算出这些元素的变化区间。这样,根据引理1,模型(22)可以写成
(B0+EbΣbFb)(U+Fc)。
(24)
设计如下的状态反馈控制器
U=KX-Fc。
(25)
其中K是反馈增益矩阵。
系统(24)在控制器(25)作用下的闭环系统为

(26)
可以得到如下定理。
定理1对于满足条件(23)的系统(22),如果存在实对称正定矩阵Q、正常数α,β和矩阵M使下面的LMI成立,则系统(22)在控制器(25)作用下得到的闭环系统(26)对平衡状态X0=0是渐近稳定的。

(27)
证明:由式(26)可知X0=0是闭环系统的平衡状态。要使卷绕系统能够实现对张力和速度的渐近跟踪,需要系统(26)在X0=0是渐近稳定的。
选取Lyapunov候选函数为
V(X)=XTPX。
(28)
式中P为实对称正定矩阵。将式(28)沿轨迹(26)对时间求导,经整理后可得
(EaΣaFa)TP+P(EaΣaFa)P+
(EbΣbFbK)T+P(EbΣbFbK)]X。
(29)
(EaΣaFa)TP+P(EaΣaFa)=
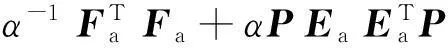
(30)
和
(EbΣbFbK)TP+PEbΣbFbK≤
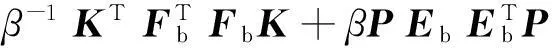
(31)
其中α,β为正常数,将式(30)和式(31)代入式(29)有
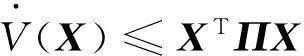
(32)
式中


(33)
由式(9)可知实际控制量ui=Ui+usi,(i=0,1,2),通过式(14)、式(16)和式(20)可以计算出usi,未知干扰和系统不确定性带来的影响通过控制量Ui进行抑制,其总体的控制结构如图3所示。
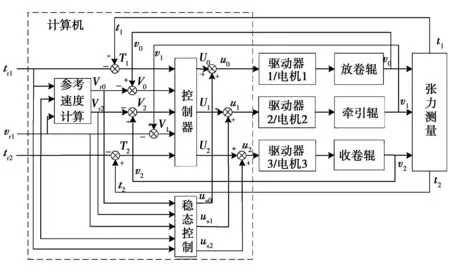
图3 三电机卷绕系统控制框图Fig.3 Block diagram of three-motor winding system
3实验研究
3.1仿真实验研究
为了验证本文所设计的鲁棒控制器的有效性,采用Matlab对控制系统进行仿真,并与常规的分散PID控制进行比较。

在控制器设计时,考虑了杨氏模量和摩擦系数在上述标称值的±30%范围内波动,半径和参考值的变化范围如下:
(34)

首先假设杨氏模量和摩擦系数为标称值,牵引辊初始给定值vr1为0.5m/s,3s时突加到1m/s,放卷张力初始值tr1为10N,1s时突加到15N,收卷张力初始值tr2为15N,2s时突减到10N,采用PID控制和鲁棒控制时的响应曲线如图4所示。
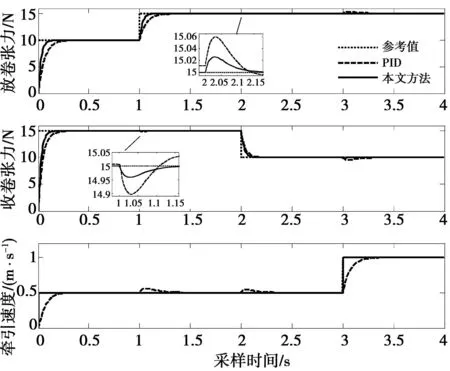
图4 标称参数下张力和速度仿真曲线Fig.4 Simulation curves of the tensions and velocity with the nominal parameters
由图4可以看到,与PID控制相比,采用本文所提出的鲁棒控制方法张力和速度能更快、更稳定的跟随设定值。当速度突变时,PID控制对放卷和收卷张力影响明显;收、放卷张力变化对速度也有明显的影响。而采用鲁棒控制时,无论放卷张力变化还是收卷张力变化对速度的影响都不明显;当放卷张力或者速度发生变化时,收卷张力有很小的变化,当收卷张力变化时,甚至采用PID控制时放卷张力看不到明显变化。表1统计了两种控制方式下张力和速度的相对最大变化值(括号中的数表示出现的时间)。由表1可以看出采用本文提出的鲁棒控制方法,张力和速度的最大变化比PID控制时小很多。

表1 仿真中设定值改变时张力和速度最大变化统计
为了验证本文方法的鲁棒性,假设杨氏模量E、摩擦系数bfi和转动惯量Ji(i=0,1,2)等参数存在不确定性,在仿真时假设它们在标称值上下30%范围内随机变化(实际应用中这些参数的不确定性不可能有如此强烈)。图5显示了杨氏模量E、摩擦系数bf0和转动惯量J0的变化曲线,限于篇幅,其他参数未一一显示。在该条件下,PID控制和鲁棒控制的效果见图6。
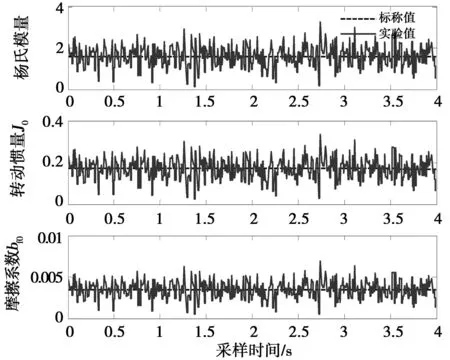
图5 部分系统参数变化曲线Fig.5 Change curves of some system parameters
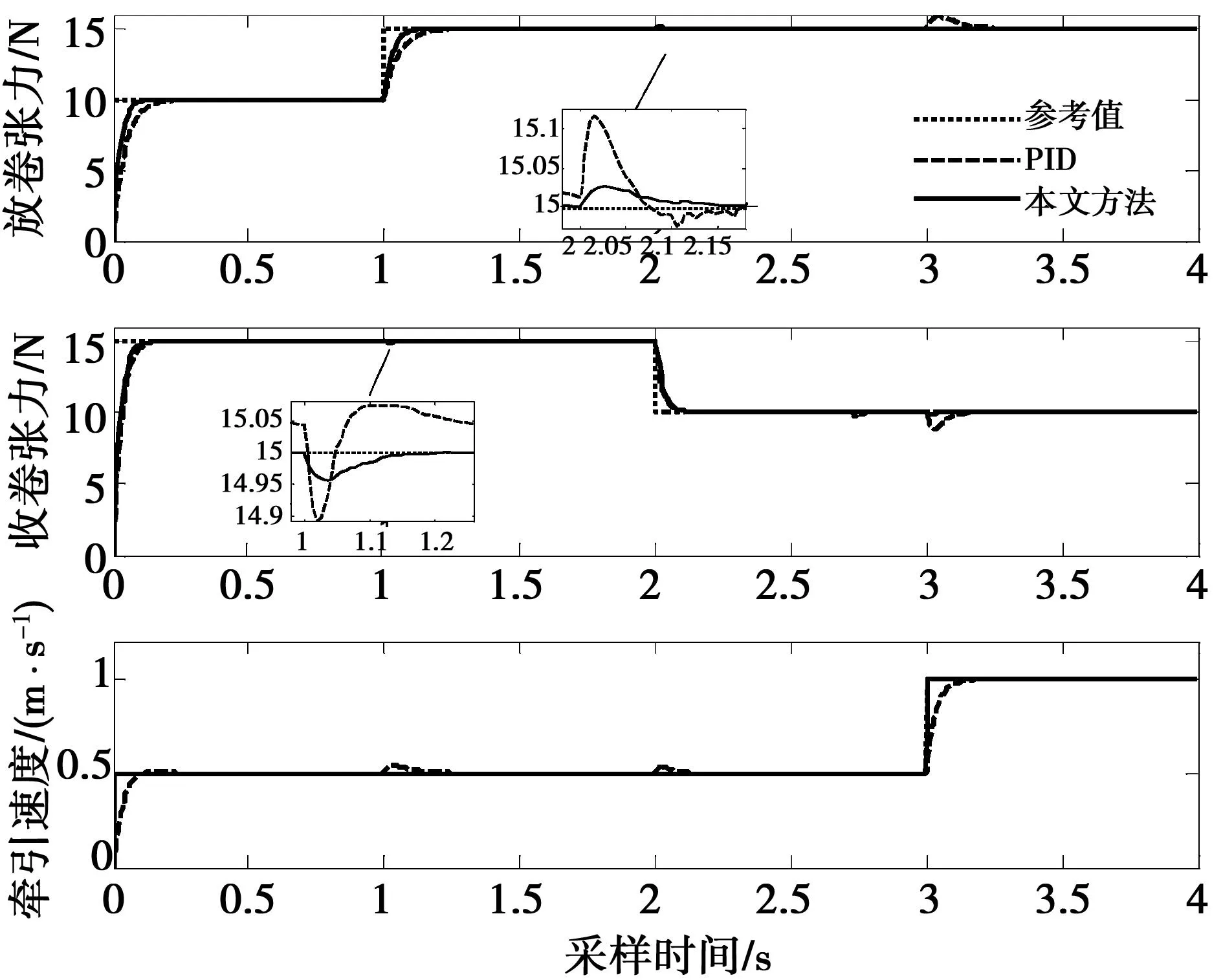
图6 不确定参数下张力和速度突变的响应曲线Fig.6 Simulation curves of the tensions and velocity with the uncertain parameters
由图6可以看出,在参数存在不确定性的情况下,两种控制方法下张力和速度的控制效果都有一定的变差。由表1可以看出,PID控制时收、放卷张力和速度相对最大变化值增加比较明显,当速度发生变化时(3 s时),放卷张力最大变化由1.92%增加到5.98%,收卷张力最大变化由4.86%增加到11.65%。而采用本文提出的方法两者变化值分别从0.43%和1.32%增加到0.54%和1.66%,增加量并不太明显。从仿真效果来看,本文提出的方法对参数变化有较强的鲁棒性。
3.2实验研究
采用本文所提出的方法在图1所示的自制实验平台上进行实验,并与常规的PID控制方法进行对比。实验平台的收、放卷电机型号为西门子1FK7060-5AH71-1型永磁同步电机,牵引电机型号为西门子1FK7042-5AH71-1型永磁同步电机。电机速度由编码器测量,张力由科帝公司的张力传感器测量。
当牵引电机以线速度0.5 m/s,放卷和收卷张力分别为10 N和15 N稳定运行后,开始采集数据。20 s时将放卷张力由10 N突增到15 N,50 s时将收卷张力突减到10 N,80 s时将速度由0.5 m/s突增到1 m/s,PID控制和本文的方法的实验结果分别如图7、图8和表2所示。
通过对比图7和图8可以看出采用本文的方法明显减小了速度和张力间的相互影响,其结果与仿真结果相一致。给定速度为0.5 m/s时,放卷张力增大50%,采用PID控制时速度变化为15.88%,收卷张力减小50%时,速度变化为26.72%。而速度增大到1 m/s,速度的调节时间约为0.1 s,放卷张力和收卷张力变化分别为5.07%和9.20%。本文设计的控制器放卷和收卷张力变化对速度的影响小得多,分别为11.30%和15.58%;速度变化的调节时间为0.06s,超调小,对收、放卷张力的影响也小很多,分别为2.84%和4.90%。表2列出了张力和速度设定值变化时的相互影响,由表2中的速度和张力最大变化值可以看出,对以PID控制,提出的鲁棒控制明显减小了张力和速度间的相互影响,抑制干扰的能力更强。综合以上分析可以看出,采用本文提出的鲁棒控制器控制时控制效果明显优于PID控制。

图7 PID控制的实验结果Fig.7 Experiment results with PID controllers

图8 本文方法的实验结果Fig.8 Experiment results with the proposed method

最大变化/%速度改变放卷张力改变收卷张力改变PID本文方法PID本文方法PID本文方法T1/tr15.072.84——3.682.31T2/tr29.204.904.533.12——V1/vr1——15.8811.3026.7215.58
5结论
本文以三电机卷绕系统为研究对象,提出了一种基于LMI的鲁棒控制器设计方法。首先,根据系统参考张力和参考速度计算出了系统的稳态控制输入和收、放卷辊的参考速度,同时得到了系统的动态误差模型;接着,在动态误差模型的基础上,提出了一种基于状态反馈的鲁棒控制器设计方法,在控制器设计过程中将设定值的改变,将收、放卷辊半径、转动惯量和受环境影响大的杨氏模量、摩擦系数等看成区间变量进行处理,因而所得的控制器对不同的工作点具有自适应能力且对参数变化具有较强的鲁棒性;此外,控制器参数只需要通过求解LMI就可得到,求解方便。最后,仿真和平台实验结果证明了本文所提出的控制方法的有效性。
参 考 文 献:
[1]HAKAN Koc,DOMINIQUE Knittel,MICHEL de Mathelin,et al.Modeling and robust control of winding systems for elastic webs[J].IEEE Transactions on Control Systems Technology,2002,10(2):197-208.
[2]VINCENT Gassmann,DOMINIQUE Knittel.Robust PI-LPV tension control with elasticity observer for roll-to-roll systems[C]//15th IFAC World Congress on,August 28-September 2,2011: 8639-8644.
[3]VINCENT Gassmann,DOMINIQUE Knittel,PRABHAKAR R Pagilla,et al.Fixed-orderHtension control in the unwinding section of a web handling system using a pendulum dancer[J].IEEE Transactions on Control Systems Technology,2012,20(1):173-180.
[4]茹锋,茹媛,胡飞虎.柔性成型生产中电机模糊张力控制技术研究[J].电机与控制学报,2011,15(2): 89-93.
RU Feng,RU Yuan,HU Feihu.Research on tension control technology based on fuzzy control algorithm[J].Electric Machines and Control,2011,15(2):89-93.
[5]刘星桥,唐琳,朱丽婷.模糊自抗扰控制的三电机同步协调系统[J].电机与控制学报,2013,17(4): 104-109.
LIU Xinqiao,TANG Lin,ZHU Liting.Three-motor synchronous control system based on fuzzyactive disturbances rejection control[J].Electric Machines and Control,2013,17(4): 104-109.
[6]贺建军,喻寿益,钟掘.板带钢平整机张力-速度解耦控制[J].控制与决策,2003,18(5): 522-526,544.
HE Jianjun,YU Shouyi,ZHONG Jue.Tension-speed decoupling control of temper mill for plate-strip steet[J].Control and Decision,2003,18(5): 522-526,544.
[7]白锐,佟绍成,蔡天佑.连续退火机组张紧辊带钢张力的建模及解耦控制[J].控制理论与应用,2013,30(3):392-397.
BAI Rui,TONG Shaocheng,CHAI Tianyou.Modeling and decoupling control for the strip tension of bridling roll in the continuous amnealing line[J].Control theory & Application,2013,30(3):392-397.
[8]CLAVEAU F,CHEVREL P,KNITTEL K.A 2DOF gain-scheduled controller design methodology for a multi-motor web transport system[J].Control Engineering Practice,2008,16:609-622.
[9]DOMINIQUE Knittel,EDOUARD Laroche,DANIEL Gigan,et al.Tension control for winding systems with two-degrees-of-freedomHcontrollers[J].IEEE Transactions on Industry Applications,2003,39(1):113-120.
[10]DOU Xijiang,WANG Wilson.Robust control of multistage printing systems [J].Control Engineering Practice,2010,18: 219 -229.
[11]ANDREW Kadik,WILSON Wang.Adaptive force control of in web handling systems[J].Intelligent Control and Automation,2012,3: 329 -336.
[12]Janabi-Sharifi F.A neuro-fuzzy system for looper tension control in rolling mills[J].Control Engineering Practice,2005,13:1-13.
[13]CHEN Chiehli,CHANG Kuoming,CHANG Chihming.Modeling and control of a web-fed machine[J].Applied Mathematical Modelling,2004,28 :863-876.
[14]ABJADI N R,SOLTANI J,ASKARI J,et al.Nonlinear sliding-mode control of a multi-motor web-winding system without tension sensor[J].IET Control Theory and Applications,2009,3(4):419-427.
[15]PRABHAKAR R Pagilla,NILESH B Siraskar,RAMAMURTHY V Dwivedula.Decentralized control of web processing lines[J].IEEE Transactions on Control Systems Technology,2007,15(1):106-117.
[16]王雅文,宫云战,肖庆,等.扩展区间运算的变量值范围分析[J].北京邮电大学学报,2009,32(3) :36-41.
WANG Yawen,GONG Yunzhan,XIAO Qing,et al.Introduction of interval analysis[J].Journal of Beijing University of Posts and Telecommunications,2009,32(3):36-41.
[17]LU Junguo,CHEN Yangquan.Robust stability and stabilization of fractional-order interval systems:an LMI approach[J].IEEE Transactions on Automatic Control,2009,54 (6) :1294-1299.
[18]申涛,王孝红,袁铸钢.一类不确定系统的鲁棒稳定性分析[J].自动化学报,2007,33(4) : 426-427.
SHEN Tao,WANG Xiaohong,YUAN Zhugang.Robust stability for a class of uncertain system[J].Acta Automatica Sinica,2007,33(4) : 426-427.
[19]Silviu-Inlian N,ROGELIO L.On the passivity of linear delay systems[J].IEEE Transactions on Automatic Control,2001,46(3): 460-464.
[20]BOYD s,GHAOUI L E,BALAKRISHNAN V.Linear matrix inequalities in systems and control theory[M].Philadelphia:Society for Industrial Mathematica,1994.
(编辑:刘琳琳)
State feedback robust control for three-motor winding system—LMI approach
HOU Hai-liang1,2,NIAN Xiao-hong1,PENG Zhi1,WANG Zhong1
(1.School of Information Science and Engineering,Central South University,Changsha 410004,China;2.School of Information,Hunan University of Humanities,Science and Technology,Loudi 417000,China)
Abstract:For the multi-motor winding system with strong coupling,uncertainties and nonlinearities,a global robust control strategy based on linear matrix inequality (LMI) was proposed.Firstly,a method for computing the equilibrium control inputs and reference speeds based on the mathematic model of the winding system was given,and the variation dynamic model was derived.Then,in order to cope with the uncertain and time-varying parameters existing in the winding system,interval matrix was introduced.Sufficient condition of closed-loop winding system robustly asymptotic stability was derived based on Lyapunov stability theory and the result was presented in terms of the LMI.Finally,the effectiveness and robustness of the proposed method was validated by some computer simulation and experimental setup experiments.
Keywords:winding system; linear matrix inequality (LMI); state feedback; interval variable; robustly asymptotic stability
收稿日期:2015-03-31
基金项目:国家自然科学基金(61473314,61403425,61321003,61472135);娄底市科技计划项目(2015KJ012);湖南省重点建设学科项目
作者简介:侯海良(1980—),男,博士研究生,研究方向为多电机系统协调控制、复杂系统建模与优化; 年晓红(1965—),男,教授,博士生导师,研究方向为交流技术与传动控制,多电机协调控制;
通信作者:侯海良
DOI:10.15938/j.emc.2016.07.015
中图分类号:TP 273
文献标志码:A
文章编号:1007-449X(2016)07-0111-08
彭智(1991—),男,硕士研究生,研究方向为多电机协调控制;
王忠(1991—),男,硕士研究生,研究方向为多电机协调控制。
