信号稀疏分解理论在轴承故障检测中的应用*

张新鹏，胡茑庆，程　哲，胡　雷，陈　凌

(国防科技大学 装备综合保障技术重点实验室， 湖南 长沙　410073)



信号稀疏分解理论在轴承故障检测中的应用*

张新鹏，胡茑庆，程哲，胡雷，陈凌

(国防科技大学 装备综合保障技术重点实验室， 湖南 长沙410073)

摘要：将信号稀疏分解理论引入到轴承故障检测问题中，提出新的轴承故障检测方法。通过字典学习的方式可有效实现轴承正常状态振动信号稀疏表示的超完备字典。利用该字典只适用于轴承正常状态信号稀疏分解的特点，将待分析信号在该字典上展开，通过比较信号稀疏表示误差与所设定阈值的关系来判断轴承对应的状态，从而实现轴承的故障检测。实验结果表明：当误差阈值设置合理时，该方法可有效地判断出轴承是否发生故障。

关键词：轴承故障检测；稀疏分解；字典学习；稀疏表示误差

由于材料缺陷、制造误差和运行环境等因素以及疲劳、老化等效应，旋转机械设备在运行过程中发生故障和损伤不可避免。而轴承作为旋转机械中最常用和最重要的关键部件之一，一旦发生故障，轻则导致设备停机影响工作效率，造成经济损失，重则会出现极端的危险事故，危及整套设备和工作人员的安全。因此，对于旋转机械设备中轴承运行状态的监控就显得尤为重要。

对于现代设备健康监控而言，首先需要解决的便是故障的检测问题，即在设备发生故障时能够及时地发现并提醒工作人员采取相应措施，从而降低故障所带来的危害。目前常用的轴承故障检测方法主要围绕着振动信号而展开，即通过安装在轴承座或箱体上的振动传感器来监测轴承的振动信号，通过分析振动信号来判断轴承状态。Zhu等[1]将零空间匹配法和S变换相结合来处理轴承振动数据，实现轴承故障的检测；Zhang等[2]将经验模式分解法和支持向量机相结合，通过计算轴承振动信号组合熵实现故障检测和分类；Faghidi等[3]提出了一种高阶能量解析算子，并将其用于强噪声背景下的轴承振动信号分析中，得到了较好的故障检测效果；Zhang等[4]基于窄带干扰消除来提取轴承振动信号中的周期脉冲信号，提高了传统方法如快速傅里叶变换等对轴承故障早期检测和退化状态分析的能力；Dae等[5]将经验模式分解法、最小熵反褶积、Teager-Kaiser能量算法以及遗传算法等结合起来，增强了峭度对振动信号的敏感度，提高了基于峭度指标的轴承故障检测方法的性能。在振动信号分析方法中，利用不同状态信号某些特征的区别来实现轴承故障检测是常用的一种较为简单和准确的，可实现轴承故障快速在线检测的方法[6-9]。特征参数的选择直接影响着故障检测效果，然而在信号分析过程中，优秀特征参数的选择往往是比较困难的。

1信号稀疏分解理论

为了更加灵活、简洁和自适应地表示信号，1992年，Coifman等[10]提出了稀疏分解的概念。稀疏分解理论认为，分解结果越稀疏则越接近信号的本质或内在结构。信号的稀疏表示(分解)能有效提取信号的本质特征，有利于信号的后续处理，可从本质上降低信号处理成本。因此，在数字信号处理应用中，人们总是用信号在某个域上的稀疏逼近取代原始数据表示。目前，稀疏表示被广泛应用于信号处理和图像处理的各个领域，如雷达成像处理、图像压缩、音频压缩、视频信号压缩、噪声抑制、盲源分离、自动控制、地震数据处理、系统辨识、轮廓识别、人脸识别等[11-18]。

给定一个超完备集合：

其中，K个元素是张成整个Hilbert空间H=RN的单位向量，若K>N，则称集合G为过完备字典，其中的元素称为原子。对于任意的信号f∈H，在G中选择m个原子对其做m项逼近，即

(1)

其中，Im是原子gγ下标的集合，cγ是原子gγ对应的系数。定义逼近误差为：

(2)

由于m远小于空间H的维数N，式(2)定义的逼近称为信号f的稀疏逼近，{cγ}γ∈Im为信号f在字典G上的稀疏表示系数。稀疏表示系数可通过匹配追踪(MatchingPursuit，MP)等方法来计算[19]。设D为超完备字典中的原子以向量形式排列组成的矩阵，c为稀疏表示系数{cγ}γ∈Im对应的向量，则式(1)可写为：

fm=D·c

(3)

可以看出，超完备字典直接影响着信号的稀疏逼近误差。按照适用范围的不同，超完备字典可分为两类：无特定使用对象的固定字典和通过训练得到的有特定使用对象的字典。固定字典的适用范围广泛，但是对信号的稀疏化程度较低，且逼近误差较大；通过训练得到的字典，由于在字典学习过程中利用了训练样本的结构和特征等信息，因此具有较好的稀疏逼近效果，但是使用范围十分有限，仅对与训练样本状态相同的信号有效。目前常用的字典学习方法主要有最优方向法(MethodofOptimalDirections,MOD)[20-21]和K奇异值分解(K-SingularValueDecomposition，K-SVD)法[22-23]等。现使用K-SVD方法来训练可稀疏表示正常状态信号的超完备字典。

2故障检测方法

由字典训练的原理可知，对于通过训练得到的字典，其只对特定信号(与训练样本类型相同的信号)具有较好的稀疏分解性能，而对异于训练样本类型的信号则不适用。设D为利用轴承正常运行过程中采集到的历史数据，通过字典学习的方式得到的超完备字典。D只适用于正常状态信号的稀疏分解，但不适用于其他状态信号的分解。设D中包含M个原子，每个原子的维数均为N，即D∈RN×M。在字典D中选择m个原子对信号x∈RN做m项逼近。

(4)

其中，di表示字典中的第i个原子，ci表示信号x∈RN在原子di上的展开系数。将式(4)转化为矩阵形式，则有：

xm=D·c

(5)

则易知展开系数向量c中非零项个数为m。

计算此时xm对信号x∈RN的逼近误差，即

(6)

将式(5)带入式(6)，则可得信号x在字典D上的稀疏分解误差为：

(7)

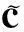
(8)

当信号x对应轴承正常状态时，由于字典D是使用轴承正常状态信号训练得到的，则此时δm应较小；而当信号x对应轴承故障状态时，由于字典D并不适用于故障状态信号的稀疏分解，因此相应的δm应较大。利用不同状态信号在字典D上稀疏表示误差的这种差异，实现轴承故障状态的检测。

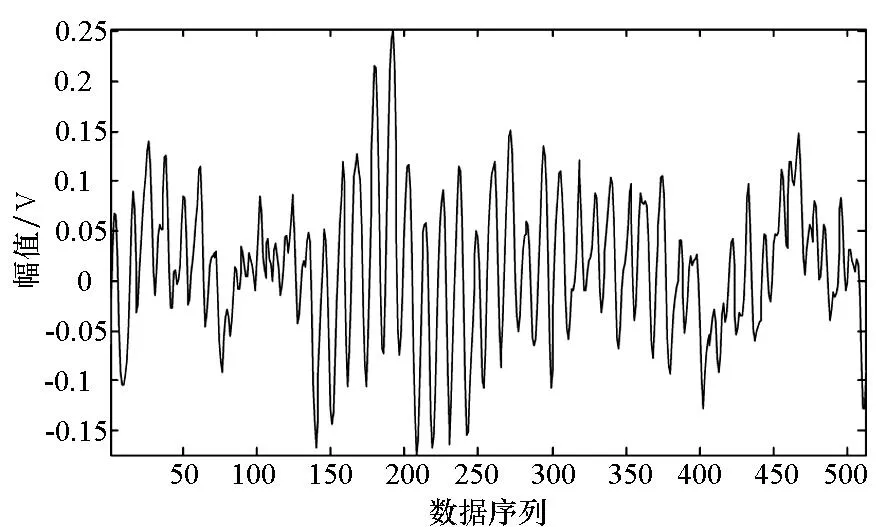
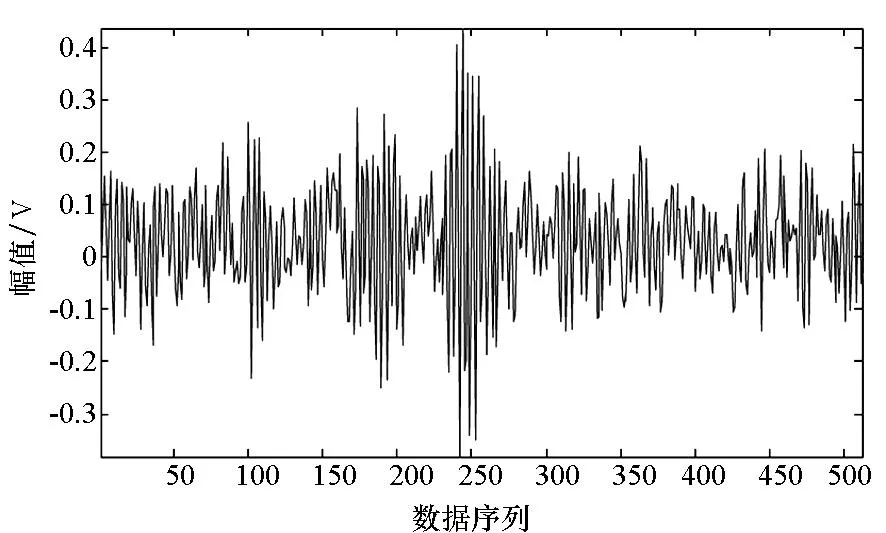
图1直观地说明了不同状态信号在字典D(由轴承正常状态样本训练所得的超完备字典)上稀疏表示误差的这种差异。图1(a)表示轴承正常状态信号；图1(b)表示轴承故障状态信号；图1(c)和图1(d)分别表示正常状态信号和故障状态信号在字典D上进行稀疏分解，对应的信号重构结果。上述信号长度均为512，均来自于6205-2RSJEKSKF深沟球轴承(数据来源于凯斯西储大学轴承实验中心，信号采样频率为12K)。字典训练时设置的信号稀疏度为10，使用MP作为信号重构算法，参与信号重构的原子个数设置为10。从图1中可以看出，正常状态信号的稀疏表示误差为0.62，明显小于故障状态信号的稀疏表示误差(2.32)。利用这种稀疏表示误差的差异，便可判断轴承状态，实现故障的检测。

(a) 正常状态信号(a) Signal in normal state

(b) 故障状态信号(b) Signal in fault state

(c) 正常状态信号重构结果(重构误差：0.62)(c) Reconstructed result of signal in normal state(reconstruction error: 0.62)

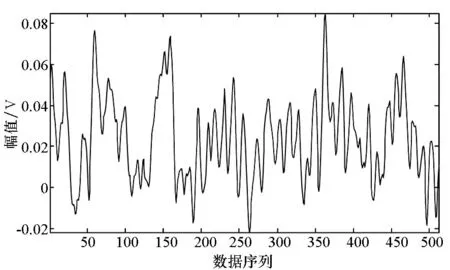
(d) 故障状态信号重构结果(重构误差：2.32)(d) Reconstructed result of signal in fault state(reconstruction error: 2.32)图1　不同状态振动信号在由正常状态样本训练所得字典上的稀疏分解结果Fig.1　Decomposition results of vibrationsignals in different states on dictionarytrained by samples in normal state

综上可得基于信号稀疏分解的轴承故障检测方法，其实现过程如图2所示，具体步骤如下：

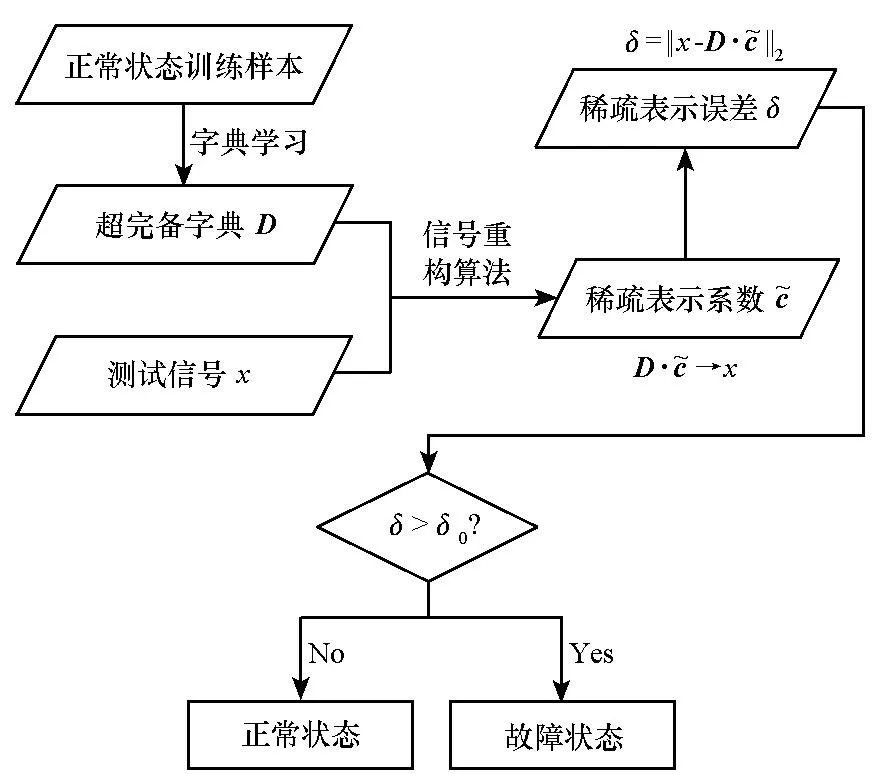
图2　基于信号稀疏分解的轴承故障检测方法流程图Fig.2　Flow chart of bearing fault detection methodbased on signal sparse decomposition

1)采集正常状态下的数据得到训练样本。

2)通过字典学习方式训练得到对应于正常状态信号的稀疏表示字典D。

3)确定稀疏表示误差阈值δ0。

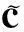
5)判断待检测信号对应的轴承状态：

当δ>δ0时，判断轴承处于故障状态；

当δ≤δ0时，判断轴承处于正常状态。

需要说明的是，由于在设备实际运行过程中，故障发生的概率是比较小的，并且故障类型较多，因此一般很难获取充足的包含足够故障信息的故障样本。而设备的正常运行是常态，因此可获取大量的正常状态信号样本，这对于字典学习是很有利的。这便是使用轴承正常运行状态样本来训练字典的原因。

3实验验证

使用6205-2RSJEKSKF深沟球轴承不同状态的振动数据对进行实验验证(数据来源于凯斯西储大学轴承实验中心[24]，信号的采样频率为12K)。

采集正常状态下轴承的振动数据作为训练样本，以此来训练对应于正常状态的稀疏表示字典。每个训练样本的数据长度均为512，训练样本个数为20 480。这些训练样本按照转速和负载的不同，又可分为四类，见表1。

表1　正常状态训练样本

利用表1中的训练样本，采用K-SVD方法训练得到可稀疏分解正常状态信号的超完备字典矩阵Dnormal，字典训练时的相关参数设置如下：字典原子个数为1024，稀疏分解原子个数为10，循环次数为20，初始字典从训练样本中选择。则可得字典矩阵Dnormal∈RN×M，N=512，M=1024。

测试样本包含800个正常状态样本和1200个故障状态样本，每个样本长度均为512。轴承故障状态包括三类：内环故障、外环故障以及滚动体故障。故障均为单点故障，通过在内环、外环以及滚动体上使用电火花加工直径为0.533mm，深度为0.279mm的故障点来模拟，实验中所用测试样本及其运行参数见表2。

将表2中的四种状态振动信号分别在超完备字典Dnormal上展开(均使用10个原子参与信号分解)，使用MP作为信号重构算法，计算相应的稀疏表示误差，结果如图3所示。

从图3中可以看出，正常状态振动信号对应的稀疏表示误差和三种故障状态振动信号对应的稀疏表示误差可以明显地区分开来，这意味着按照所提思路实现轴承故障检测是可行的。若要实现故障检测，则需要确定合适的阈值来区分正常状态和故障状态对应的稀疏表示误差，阈值的设定对检测结果应具有重要影响。下面分析不同阈值下的故障检测结果。

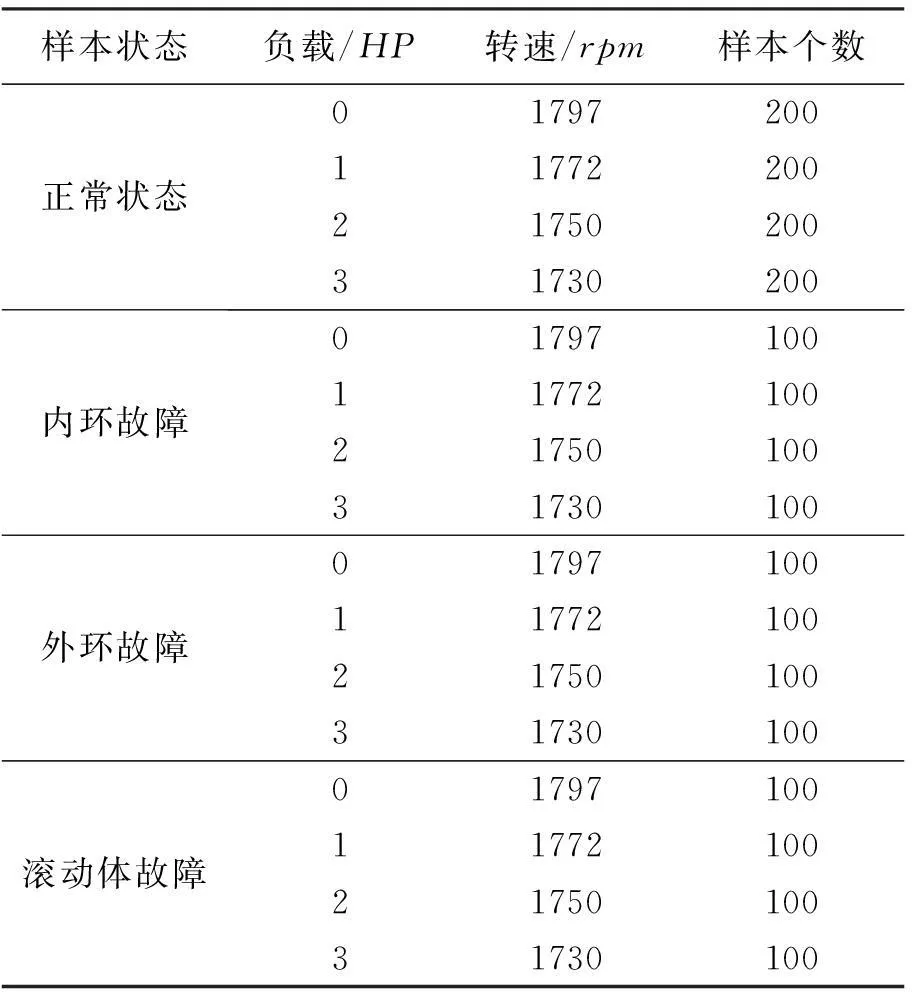
表2　测试样本

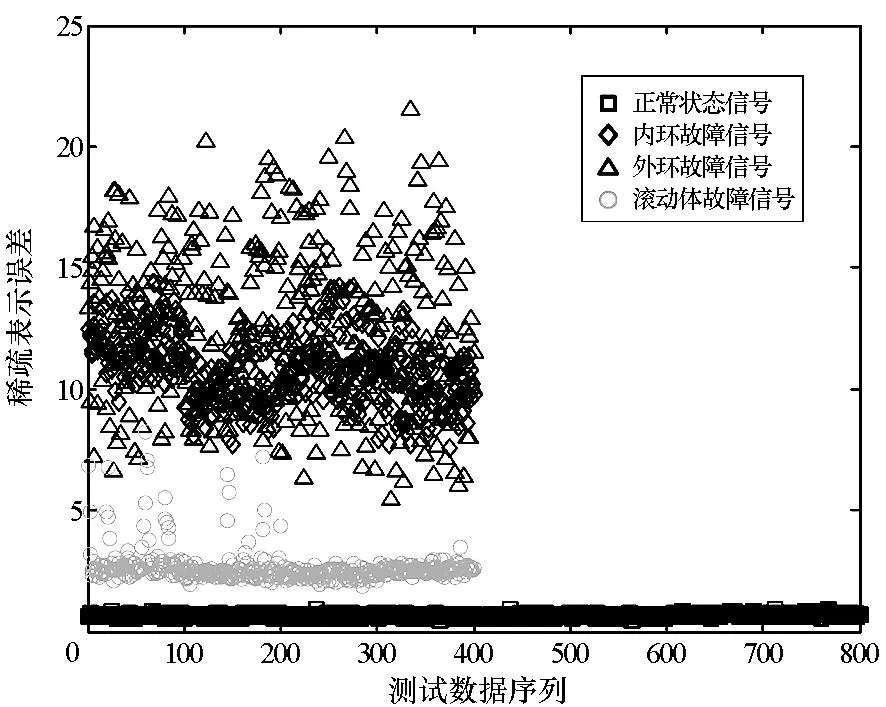
图3　不同状态振动信号对应的稀疏表示误差Fig.3　Sparse representation errors corresponded tovibration signals in different states

对表2中的测试样本进行故障检测，使用MP作为信号重构算法，使用10个原子来重构信号，则不同阈值对应的故障检测结果如图4所示。故障检测结果用故障检测率和虚警率来表示。故障检测率定义为准确检测出的故障样本个数与实际故障样本总数的比值；虚警率定义为实际为正常状态却被判定为故障状态的样本个数与实际正常状态样本总数的比值。

从图4中可以看出，阈值的选择直接影响着故障检测结果。随着稀疏表示误差阈值的增大，故障检测率和虚警率均降低。阈值越小，故障检测率就越高，同时虚警率也就越大。优秀的故障检测结果应在保证较高故障检测率的同时，具有尽可能低的故障虚警率。因此，从图4中可以看出，当阈值取值范围为[0.9，2]时，故障检测结果是最优的，此时故障检测率可达到100%，虚警率为0。

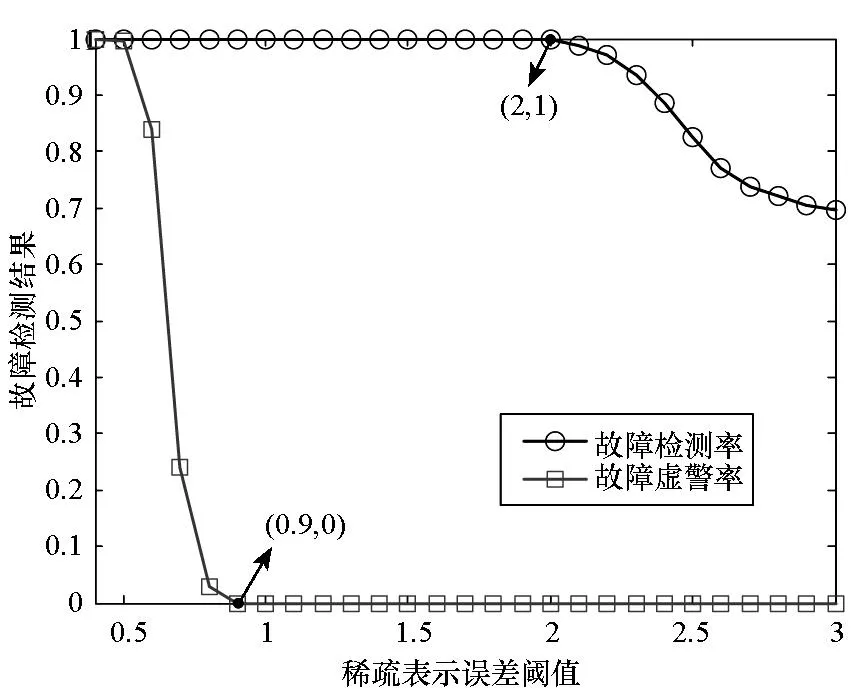
图4　故障检测结果Fig.4　Fault detection results

实际故障检测时，稀疏表示误差阈值可根据先验知识来确定。从轴承正常状态振动数据样本中，随机选择若干个信号(以2000个为例)，将其在字典Dnormal上分解，参与信号分解的原子个数设置为10个，信号重构算法使用MP算法，计算相应的稀疏表示误差e，结果如图5所示。

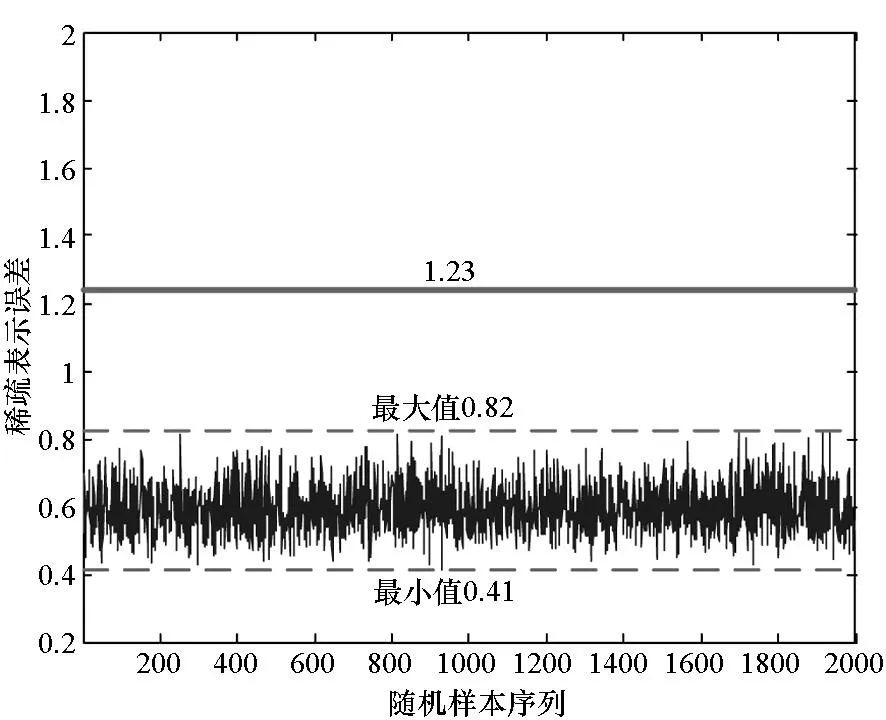
图5　正常状态信号的稀疏表示误差Fig.5　Sparse representation error ofsignals in normal state

从图5中可以看出，稀疏表示误差在一个较小的范围内波动，总体稳定。由此可近似地确定，当分解原子个数为10时，阈值δ0的下界，即δ0>max(e)。考虑到误差可能的波动情况，按照式(9)所示原则设置阈值。

δ0=max(e)+[max(e)-min(e)]

=2·max(e)-min(e)

(9)

在上述实验中，按照该阈值设置原则，可得阈值δ0=1.23(如图5中粗实线所示)，此时阈值处于[0.9, 2]范围内，相应的故障检测结果将达到最优，这也说明按照上述原则来设置阈值是合理的。

需要说明的是，利用正常状态信号可基本确定稀疏表示误差阈值的下界，上述原则在此基础上设定阈值。实际中，设备一般是处于正常运行状态的，发生故障后且在故障状态下运行的时间是比较短的，因此采集大量正常状态信号是较为容易的，而要得到较为完备的故障状态信号则较为困难。如果能够得到故障状态信号，则可根据其在字典Dnormal上的稀疏表示误差来确定阈值的上界。阈值在上述上界和下界之内设定会更为可靠。考虑到实际中往往缺乏故障状态信号，因此按照前述的阈值设定原则，即在下界的基础上设置合适的稀疏表示误差阈值。

在上述实验过程中，信号分解时使用了字典中的10个原子，实际上，参与信号分解的原子并不局限于10个，下面分析参与信号分解的原子个数变化时，对表2中测试样本的故障检测结果。分解原子个数影响着信号的稀疏表示误差，进而影响阈值δ0的设置。为便于比较，均按照前述的阈值设置原则设定不同分解原子个数下的稀疏表示误差阈值，其中随机选择的正常状态样本个数为2000。信号重构算法使用MP算法，计算不同分解原子个数对应的故障检测率和完成所有测试样本检测的总耗时，实验所用计算机配置双核Inter(R)Core(TM)2DuoCPU，E7400 @2.80GHz，1.96GB内存。检测结果如图6所示。

从图6中可以看出，参与信号分解的原子个数对故障检测率几乎没有产生影响，当分解原子取不同数量时，轴承故障检测率均维持在较高的水平。而随着分解原子的增多，完成表2中2000个测试样本检测的计算耗时近似呈现线性增长的趋势。因此，在进行故障检测时，应尽可能选择较少的原子来参与信号分解。

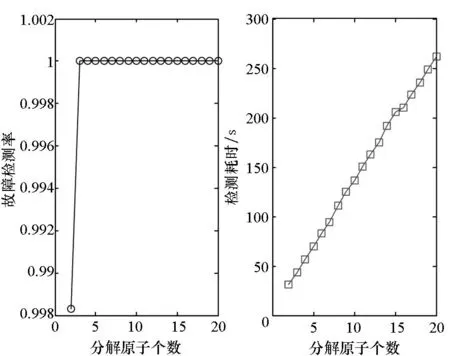
图6　不同分解原子个数下的故障检测结果Fig.6　Fault detection results with different numbers ofatoms involved in signal decomposition

基于正常状态和故障状态振动信号在字典Dnormal上稀疏表示误差之间的差异来实现轴承故障的检测。这种差异越大，越容易区分正常状态和故障状态，则该方法的故障检测性能越好。目前众多常用的故障检测方法则是选择若干特征参数，利用正常状态和故障状态信号对应特征值的差异实现故障检测。同样地，这种特征值的差异越大，越容易区分正常状态和故障状态，则该特征参数对应的故障检测性能就越好。常用的特征参数主要包括均值、方根幅值、均方根值、方差、绝对平均值、峰值、峰峰值、裕度因子、峰值因子、波形因子、脉冲因子、偏度指标和峭度指标等[24]，见表3。

表3　常用特征参数

注：N为数据总数，x为样本序列，i为数据索引。

为了便于对比本文方法与基于特征参数的故障检测方法的故障检测性能，设振动信号在字典Dnormal上的稀疏表示误差为T0，统一起见，以下也称T0为特征参数。根据前述分析可知，对于特征参数Tk(k=0,1,2,…,13)，故障状态信号对应特征值与正常状态信号对应特征值的差别越大，则基于该特征参数的故障检测方法的故障检测性能就越好。计算表2中所示四种状态下测试样本对应特征值Tk(k=0,1,2,…,13)的平均值，结果如图7所示。

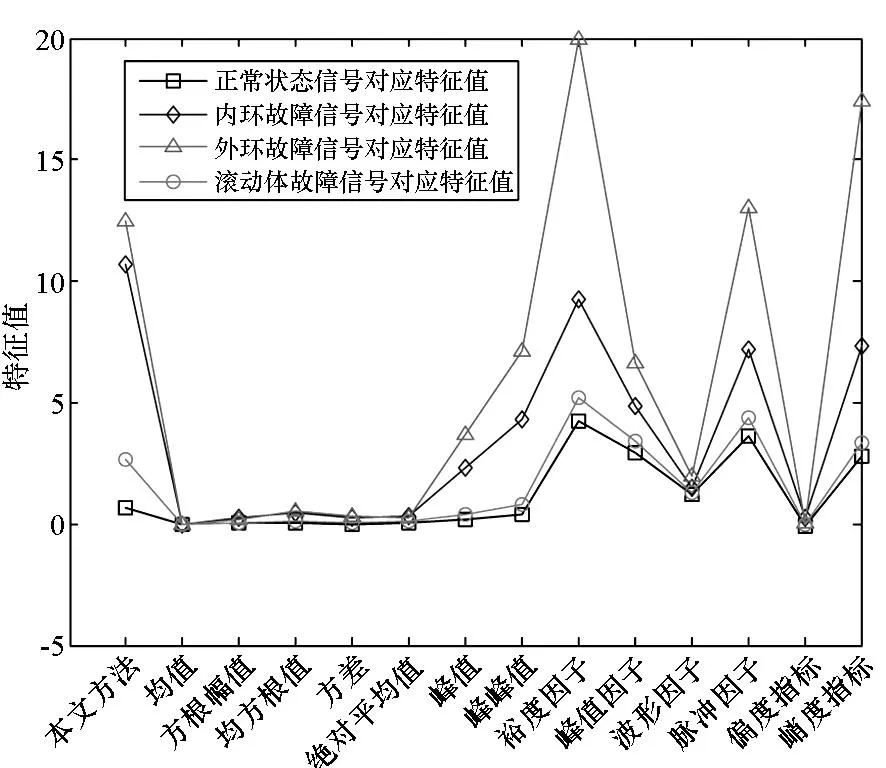
图7　不同状态信号对应的特征值Fig.7　Values of parameters corresponded tosignals in different states

从图7中可以看出，本文方法中，各种状态对应的特征值差别是最为明显的，因此故障状态和正常状态是易于区分的。正常状态信号与内外环故障对应的峰值、峰峰值、裕度因子、峰值因子、脉冲因子和峭度指标之间存在较为明显的差别，意味着内外环故障与正常状态较易区分；而滚动体故障和正常状态对应的特征值的差别却不太明显，导致滚动体故障与正常状态不易于区分。因此，通过对比可以看出，本文方法的故障检测性能要优于基于上述特征参数的故障检测方法。

4结论

基于信号稀疏分解理论的轴承故障检测方法引入了一种新的特征参数，根据正常状态轴承和故障状态轴承对应的该类参数值的不同，实现轴承故障的检测。实验结果表明，在阈值设置合理的情况下，该方法具有较好的故障检测效果，且相对于基于常用的特征参数的方法，也具有更好的故障检测性能。阈值的设定直接影响着故障检测的结果，而对于阈值的选择，可以参考字典对正常状态信号的稀疏表示误差来确定；如果能得到一些故障样本，则有助于阈值范围的进一步确定。构造的正常状态信号稀疏表示字典可实现正常状态信号稀疏分解，但无法对故障状态信号进行有效的稀疏分解，这是所提故障检测方法的基础。另外，从故障检测原理可以看出，当能够获得足够故障样本时，可扩展到故障识别方向。利用训练所得字典仅可实现对应状态信号稀疏分解的特性，可以进一步实现轴承故障模式判断，这也是下一步的研究方向。

参考文献(References)[1]Zhu D, Gao Q W, Sun D, et al. A detection method for bearing faults using null space pursuit and S transform [J]. Signal Processing, 2014, 96: 80-89.

[2]ZhangXY,LiangYT,ZhouJZ,etal.Anovelbearingfaultdiagnosismodelintegratedpermutationentropy,ensembleempiricalmodedecompositionandoptimizedSVM[J].Measurement, 2015, 69: 164-179.

[3]FaghidiH,LiangM.Detectionofbearingfaultdetectionfromheavilycontaminatedsignals:ahigher-orderanalyticenergyoperatormethod[J].JournalofVibrationandAcoustics, 2015, 137(4): 041012.

[4]ZhangXH,KangJS,BechhoeferE,etal.Enhancedbearingfaultdetectionanddegradationanalysisbasedonnarrowbandinterferencecancellation[J].InternationalJournalofSystemAssuranceEngineeringandManagement, 2014, 5(4): 645-650.

[5]KwakDH,LeeDH,AhnJH,etal.Faultdetectionofroller-bearingsusingsignalprocessingandoptimizationalgorithms[J].Sensors, 2014, 14(1): 283-298.

[6]栗茂林, 梁霖, 王孙安. 基于稀疏表示的故障敏感特征提取方法[J]. 机械工程学报, 2013, 49(1): 73-80.LIMaolin,LIANGLin,WANGSunan.Sensitivefeatureextractionofmachinefaultsbasedonsparserepresentation[J].JournalofMechanicalEngineering, 2013, 49(1): 73-80. (inChinese)

[7]王国彪, 何正嘉, 陈雪峰, 等. 机械故障诊断基础研究“何去何从”[J]. 机械工程学报, 2013, 49(1): 63-72.

WANGGuobiao,HEZhengjia,CHENXuefeng,etal.Basicresearchonmachineryfaultdiagnosis—whatistheprescription[J].JournalofMechanicalEngineering, 2013, 49(1): 63-72. (inChinese)

[8]曾庆虎, 邱静, 刘冠军, 等. 小波相关特征尺度熵在滚动轴承故障诊断中的应用 [J]. 国防科技大学学报, 2007,29(6): 102-105.

ZENGQinghu,QIUJing,LIUGuanjun,etal.Applicationofwaveletcorrelationfeaturescaleentropytofaultdiagnosisofrollerbearings[J].JournalofNationalUniversityofDefenseTechnology, 2007, 29(6): 102-105. (inChinese)

[9]王炳成, 任朝辉, 闻邦椿. 基于非线性多参数的旋转机械故障诊断方法[J]. 机械工程学报, 2012, 48(5): 63-69.WANGBingcheng,RENZhaohui,WENBangchun.Faultdiagnosesmethodofrotatingmachinesbasedonnonlinearmulti-parameters[J].JournalofMechanicalEngineering, 2012, 48(5): 63-69. (inChinese)

[10]CoifmanRR,WickerhauserMV.Entropy-basedalgorithmsforbestbasisselection[J].IEEETransactionsInformationTheory, 1992, 38(2): 713-718.

[11]杜小勇. 稀疏成分分析及在雷达成像处理中的应用[D]. 长沙: 国防科学技术大学, 2005.

DUXiaoyong.Sparsecomponentanalysisandtheapplicationinradarimagingprocessing[D].Changsha:NationalUniversityofDefenseTechnology, 2005. (inChinese)

[12]NeffR,ZakhorA.Verylowbitratevideocodingbasedonmatchingpursuits[J].IEEETransactionsonCircuitsandSystemsforVideoTechnology, 1997, 7(1): 158-171.

[13]DonohoDL.De-noisingbysoft-thresholding[J].IEEETransactionsonInformationTheory, 1995, 41(3): 613-627.[14]韦泉华. 基于稀疏表示的盲信号分离算法及其改进[D]. 北京: 中国地质大学, 2006.

WEIQuanhua.Blindsourceseparationbasedonsparserepresentationanditsimprovement[D].Beijing:ChinaUniversityofGeosciences, 2006.(inChinese)

[15]ShmiloviciA,MaimonO.Applicationofadaptivematchingpursuittoadaptivecontrolofnonlineardynamicsystems[J].IEEEProceedingofControlTheoryandApplication, 1998, 145(6): 575-581.

[16]ChenS,BillingsSA,LuoW.Orthogonalleastsquaresmethodsandtheirapplicationtonon-linearsystemidentification[J].InternationalJournalofControl, 1989, 50(5): 1873-1896.

[17]JaggiS,KarlWC,MallatSG,etal.Silhouetterecognitionusinghighresolutionpursuit[J].PatternRecognition, 1991, 32(5): 753-771.

[18]PhillipsPJ.Matchingpursuitfiltersappliedtofaceidentification[J].IEEETransactionsonImageProcessing, 1998, 7(8): 1150-1164.

[19]MallatS,ZhangZ.Matchingpursuitswithtime-frequencydictionaries[J].IEEETransactionsonSignalProcessing, 1993, 41(12): 3397-3415.

[20]EnganK,AaseSO,HusoyJH.Multi-framecompression:theoryanddesign[J].SignalProcessing, 2000, 80(10): 2121-2140.

[21]EnganK,AaseSO,Hakon-HusoyJH.Methodofoptimaldirectionsforframedesign[C]//ProceedingsofInternationalConferenceonAcoustics,SpeechandSignalProcessing, 1999: 2443-2446.

[22]AharonM,EladM,BrucksteinAM.K-SVD:analgorithmfordesigningofovercompletedictionariesforsparserepresentation[J].IEEETransactionsonSignalProcessing, 2006, 54(11): 4311-4322.

[23]AharonM,EladM,BrucksteinAM.Ontheuniquenessofover-completedictionaries,andapracticalwaytoretrievethem[J].LinearAlgebraanditsApplications, 2006, 416(1): 48-67.

[24]孙闯, 何正嘉, 张周锁, 等. 基于状态信息的航空发动机运行可靠性评估[J]. 机械工程学报, 2013, 49(6): 30-37.SUNChuang,HEZhengjia,ZHANGZhousuo,etal.Operatingreliabilityassessmentforaero-enginebasedonconditionmonitoringinformation[J].JournalofMechanicalEngineering, 2013, 49(6): 30-37.(inChinese)

Application of signal sparse decomposition theory in bearing fault detection

ZHANG Xinpeng, HU Niaoqing, CHENG Zhe, HU Lei, CHEN Ling

(LaboratoryofScienceandTechnologyonIntegratedLogisticsSupport,NationalUniversityofDefenseTechnology,Changsha410073,China)

Abstract：Anewbearingfaultdetectionmethodbasedonthesignalsparsedecompositiontheorywasdeveloped.Anover-completedictionaryonwhichthebearingvibrationsignalsinnormalstatecanberepresentedsparselywastrainedbythedictionarylearningmethod.Accordingtothefactthatthisdictionaryjustcansparselyrepresentthesignalsinnormalstate,thebearingvibrationsignalinunknownstatewasdecomposedonthisdictionary.Thebearingstatewasdeterminedbycomparingtherepresentationerrorofthesignalonthedictionarywiththegivenerrorthreshold,andthenthebearingfaultdetectionwasachieved.Experimentaltestsvalidatetheeffectivenessoftheproposedmethodinbearingfaultdetectionwhensettinganappropriateerrorthreshold.

Keywords：bearingfaultdetection;sparsedecomposition;dictionarylearning;sparserepresentationerror

doi:10.11887/j.cn.201603024

收稿日期：2015-04-13

基金项目：国家自然科学基金资助项目(51375484，51205401，51475463)；国防科学技术大学博士生跨学科联合培养计划资助项目(kxk140301)

作者简介：张新鹏(1986—)，男，陕西咸阳人，博士研究生，E-mail：zhangxinpeng@nudt.edu.cn； 胡茑庆(通信作者)，男，教授，博士，博士生导师，E-mail：hnq@nudt.edu.cn

中图分类号：TP206

文献标志码：A

文章编号：1001-2486(2016)03-141-07

http://journal.nudt.edu.cn