高动态GNSS信号多普勒模拟任意阶直接数字合成器设计*

周　超，王跃科，乔纯捷，戴卫华

(国防科技大学 机电工程与自动化学院， 湖南 长沙　410073)



高动态GNSS信号多普勒模拟任意阶直接数字合成器设计*

周超，王跃科，乔纯捷，戴卫华

(国防科技大学 机电工程与自动化学院， 湖南 长沙410073)

摘要：为高精度模拟高动态条件下GNSS信号的多普勒特性，提出一种任意阶直接数字合成信号合成器的设计方法。设计任意阶直接数字合成信号合成器的结构；通过理论分析，推导各级累加器相位初值的计算公式；给出字长选择方法。经仿真验证，该方法能精确模拟GNSS信号的多普勒特性。此外，提出的直接数字合成器设计方法不受阶数的限制，可普遍应用于各类信号模拟器的设计。

关键词：高动态；GNSS信号；多普勒；任意阶直接数字合成

全球导航卫星系统(Global Navigation Satellite System, GNSS) 的应用越来越广泛，几乎涉及各行各业和生活中的各个领域[1-2]。GNSS信号模拟器可根据接收机载体与卫星的相对运动关系，模拟产生接收机接收到的GNSS信号，用于接收机的功能测试、测量精度鉴定等[3-4]，为接收机的研发、生产和测试提供低成本而有效的手段[5-6]。在高动态使用条件下的导航过程中，例如高速飞行器导航、低轨卫星定位等，卫星与接收机载体间高速、复杂的相对运动会使得接收信号产生明显的多普勒效应[7]。接收信号相对于发射信号往往存在多普勒频偏、多普勒加速度及更高阶的多普勒特征，是影响导航接收机性能的关键要素之一。因此，为了测试和评估导航接收机对高动态条件下接收信号多普勒特性的处理能力，需要利用信号模拟器精确仿真GNSS信号的多普勒特性，以模拟真实的高动态运动环境。

目前，信号合成通常采用传统直接数字合成(Direct Digital Synthesis, DDS)的一阶合成方法[8-9]。由于每个控制周期内的信号频率被看作是固定值，所以它只能模拟卫星信号多普勒频移量，无法满足高动态环境下的应用要求。为了模拟多普勒特性更高阶的特征，提高信号模拟精度，齐巍等[10]采用了二阶DDS结构，刘芊岑等[11]和Zhang等[12]采用了三阶DDS结构。然而，这些研究工作都是在特定的阶数下讨论DDS合成器的设计方法，并无文献考虑普遍问题，展开对任意阶数下DDS信号合成器设计方法的研究。

1高动态GNSS信号模型

不考虑引入的噪声，GNSS信号模型通常可

表示为：

(1)

式中，c表示信号传播速度，Ω0表示载波频率，A(t)表示信号幅度，PN(t)表示调制的伪随机码，D(t)表示信号中调制的电文比特，d(t)表示接收机与卫星间的径向距离。GNSS信号多普勒模拟最为关键的就是载波相位φ(t) =-Ω0d(t)/c的高精度实时计算与合成。在高动态条件下，径向距离d(t)的函数表达式比较复杂，通常用多项式模型进行逼近，表示为：

d(t)=p0+p1t+p2t2+…+pNtN

(2)

式中，多项式系数pn(n= 0, 1, 2, …,N)具有实际物理意义，分别代表接收机与卫星间运动学模型的各阶特征量，例如：p0等价于初始距离，p1等价于速度，p2等价于加速度的二分之一等。由此，载波相位φ(t)也可用如式(3)所示的多项式模型进行表示：

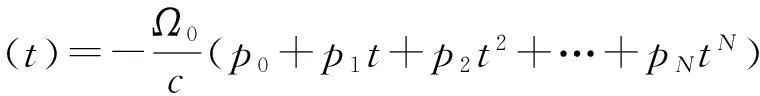
(3)

式(3)是DDS合成器模拟合成载波相位的数学基础，多项式阶数N即为DDS的阶数。给定时间区间，采用分段多项式对载波相位φ(t)进行逼近，其中多项式的分段时间间隔称为DDS合成器的控制周期。

载波相位的高精度模拟有两种方式：一种是保持较小控制周期，增大DDS的阶数，其优点是信号参数只需进行少量的计算和更新，但过高的阶数会急剧增大DDS合成器的硬件规模；另一种是保持较低的阶数，缩小DDS的控制周期，其优点是硬件规模相对较小，但要求硬件必须具备较高的计算能力，对各控制周期的信号参数进行实时计算和更新。

因此，DDS阶数及控制周期的确定需要综合考虑信号模拟精度和硬件资源情况两个方面的因素。一种可行的方案是：首先根据信号模拟器硬件的参数实时计算能力和参数配置接口的带宽，确定可接受的最小控制周期，即多项式逼近的分段时间间隔；然后根据给定的信号模拟精度要求(等同于多项式逼近的容许误差)，取满足精度要求的多项式阶数最小值作为最终的DDS阶数。

2任意阶DDS信号合成器

给定DDS阶数N，设计的DDS信号合成器结构如图1所示，共包含N+1级相位累加器(ACCumlator, ACC)。向量Φ(0)=[φ(0)(0),φ(1)(0), …,φ(N)(0)]T表示各级累加器的相位初值，在各控制周期的初始时刻，需要对Φ(0)进行实时更新。在时钟驱动下，各级累加器开始工作，Φ(k) = [φ(0)(k),φ(1)(k), …,φ(N)(k)]T表示第k个时钟周期各级累加器的相位状态值，其状态转移方程可由式(4)进行表示。

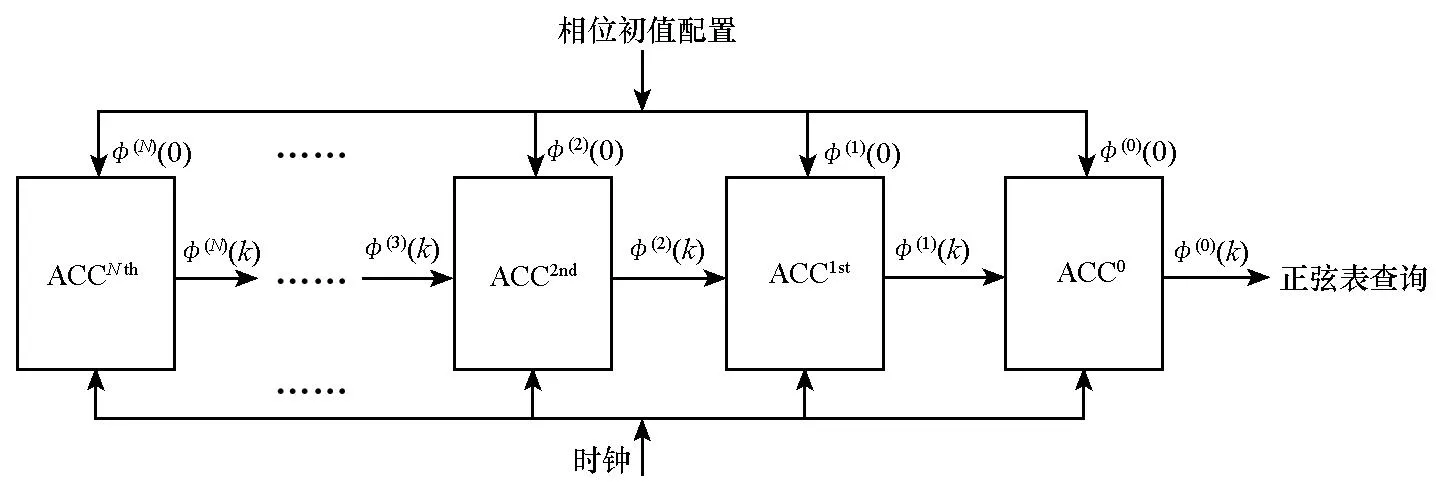
图1　N阶DDS合成器结构图Fig.1　Structure of N-order DDS synthesizer

(4)

当一个时钟周期结束时，除了最后一级累加器状态始终不变外，即φ(N)(k)≡φ(N)(0)，其余各级累加器的相位状态都会发生变化，并且相位状态值由前一个时刻此累加器与前一级累加器的相位状态值求和得到。φ(0)(k)是DDS信号合成器的相位输出，其作为正弦表的查表输入导出信号波形值。

3相位初值的计算

如图1所示的DDS信号合成器设计，首先要讨论的是各级相位累加器初值Φ(0)的计算问题。

定理对N级DDS信号合成器，第k个时钟周期的相位输出与各级累加器的相位初值满足如式(5)所示关系：

(5)

并且当N给定时，式中的系数是确定的，可通过简单计算得到。

证明：利用数学归纳法证明定理。首先，由式(4)可导出DDS各级相位状态的计算公式：

(6)

当给定阶数N，由式(6)最后一行逐次代入前一行即可得到相位输出φ(0)(k)的表达式。

显然，对1阶DDS有相位输出：

φ(0)(k)=φ(0)(0)+kφ(1)(0)

(7)

假设对N阶DDS有式(5)成立，则对N+1阶DDS，第2级相位状态φ(1)(k)可表示为：

(8)

结合式(6)可得：

(9)

根据Bernoulli自然数求幂和公式[13]：

(10)

联合式(9)和式(10)可导出N+1阶DDS的相位输出可表示为：

(11)

至此，定理证明完毕。

假设驱动DDS合成器的时钟周期为TS，由式(3)可知，在一个控制周期内，要模拟的载波相位φ(k)为：

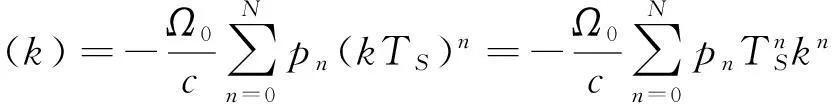
(12)

由于定理中的式(5)成立，所以通过待定系数法可建立如式(13)所示的线性方程组：

B·Φ(0)=P

(13)

式中，矩阵B和向量P均确定已知，

(14)

由此可得如图1所示DDS结构的各级累加器相位初值的计算公式为：

Φ(0)=B-1·P

(15)

4字长选取方法

DDS合成器以二进制定点数表示各阶相位状态量，字长选择是DDS设计的又一重要问题，其包括两个方面：一是各级相位初值量化字长；二是各级累加器字长。前者用于DDS启动前对式(15)计算得到的相位初值Φ(0)进行量化，其长度取决于GNSS信号各阶特征量的仿真精度要求；后者用于DDS启动后存储各级累加器的相位状态值。在选定量化字长的基础上，累加器字长取决于各相位状态值的动态范围。

相位初值量化字长的选择等价于初始相位量化误差的确定问题。假设W1=[W10,W11, …,W1N]T表示各级相位初值的量化字长，则对应的各级量化误差e=[e0,e1, …,eN]T与W1应满足：

(16)

量化误差e直接影响了GNSS信号各阶特征量的仿真精度，因此e的确定取决于设计者对各阶特征量的仿真精度要求。若给定式(2)中各阶特征量精度要求ε=[ε0,ε1, …,εN]T，则由式(13)可知，量化误差必须满足不等式：

(17)

考虑最低要求，量化误差正好满足仿真精度约束，则此时相位初值量化字长的选择方法可表述为：由e=B-1ξ计算各级量化误差，导出量化字长的最低要求W1=ceil{log2(2π/e)}；为简化硬件实现过程，各级统一采用W1中的最大值max{W1}作为量化字长。

DDS各级累加器的作用是存储信号合成过程中各级相位的状态值，累加器字长的大小决定了各级累加器开辟的存储空间容量。而当量化字长选定后，存储空间的容量直接影响各级相位状态的动态范围，累加器存储空间越大，能承受的相位动态范围也就越大。因此，累加器字长的选择完全取决于各级相位状态的动态范围要求。在一个控制周期内，若给定动态范围区间长度ΦL，则累加器字长W2= [W20,W21, …,W2N]T由式(18)进行计算：

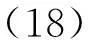
第一级累加器的相位状态就是DDS合成器的相位输出，其累加器字长W20就等于选择的量化字长。

现将提出的任意阶DDS合成器的设计步骤总结如下：

1)设计者根据要模拟的多普勒特性需求确定相位多项式的分段间隔、阶数，以及各段区间的函数表达式；

2)计算各级DDS累加器的相位初值；

3)根据各阶特征量的模拟精度要求确定各级相位初值的量化字长；

4)根据各级相位状态的动态范围确定各级DDS累加器字长。

5仿真与验证

在高动态环境下，载体接收机与导航卫星之间存在复杂的相对运动。在一个控制周期内，假设用3阶多项式描述其径向距离的变化：

(19)

式中：d0，v，α，α′分别表示初始时刻载体接收机与卫星间的径向距离、速度、加速度、加加速度。若从零时刻开始，则接收到的GNSS信号的载波相位表示为：

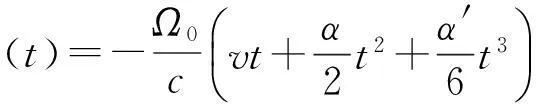
(20)

假设具体场景：载波频率Ω0=2πf0，f0=1.555 GHz；控制周期为100 ms，时钟周期为50 μs；运动模型初始参数d0,v,α,α′分别为1000 km, 2000 m/s, 1 m/s2, 60 m/s3；各特征量模拟精度要求分别为1 mm, 10 mm/s, 10 mm/s2, 100 mm/s3。为合成如式(20)所示的载波相位，按照所提出的设计方法可得DDS合成器的设计参数如表1所示。

表1　DDS合成器的设计参数

图2给出了所设计的3阶DDS信号合成器的多普勒仿真误差。由图表明，设计的合成器可以精确模拟多普勒特性的变化，在一个控制周期内，偏差不大于0.1 mHz。随着时间的推移，多普勒仿真误差呈现增长趋势，这是DDS累积误差逐渐增大所致，但此累积误差是受控的，在下一个控制周期参数更新后将被消除。

在高动态条件下，DDS合成器的阶数是GNSS信号多普勒模拟精度的决定性因素。式(19)是一个包含加加速度的运动模型，若用低于3阶的DDS合成器进行信号合成，多普勒仿真精度将会急剧下降，并且时间累积越长，差异越明显。如图3所示，在一个控制周期内，2阶DDS的多普勒仿真误差接近1.5 Hz，相对于3阶DDS增大了近15 000倍；而1阶DDS的多普勒仿真偏差接近2 Hz，相对3阶DDS增大了近20 000倍。此外，由于采用低阶DDS导致的多普勒仿真误差还会随着高阶特征量的增大而增大。如图4所示，当加加速度的取值分别为20 m/s3, 60 m/s3, 100 m/s3时，2阶DDS的多普勒仿真误差随着加加速度的增大而不断增大，并且时间累积越长，差异越明显。

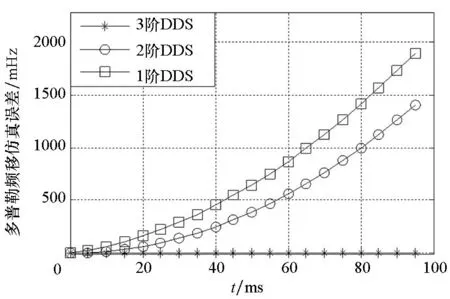
图3　不同DDS阶数下多普勒仿真误差Fig.3　Doppler simulation error in different DDS orders

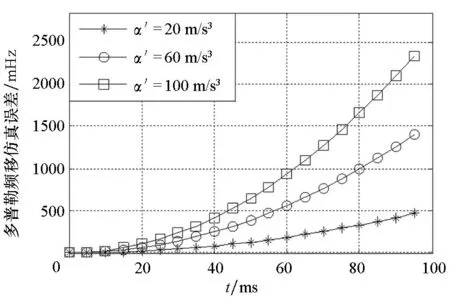
图4　二阶DDS在不同加加速度下多普勒仿真误差Fig.4　Doppler simulation error based on 2-orderDDS in different acceleration rates

6结论

高动态GNSS信号多普勒特性的精确模拟是信号模拟器必须要面临的一个关键问题，故提出一种任意阶DDS信号合成器的设计方法。基于相位多项式数学模型，设计了任意阶DDS信号合成器的结构；给出了各级累加器相位初值的计算公式；讨论了各级相位初值量化字长和各级累加器字长的选取方法。仿真实验表明，该设计方法能精确模拟GNSS信号的多普勒特性，在一个控制周期100 ms内，多普勒偏移的仿真误差不大于0.1 mHz。此外，提出的DDS设计方法不受阶数的限制，可普遍应用于各类信号模拟器的设计。

参考文献(References)[1]贺凯飞. 航空重力测量中GNSS动态定位与测速研究[J]. 测绘学报, 2015, 44(10): 1179.

HE Kaifei. GNSS kinematic position and velocity determination for airborne gravimetry [J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1179.(in Chinese)

[2]Shan Z Y, Han H Z, Jiang K. Optimization model of GNSS/pseudolites structure design for open-pit mine positioning[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(7): 2201-2208.

[3]Brown A, Gerein N, Taylor K. Modeling and simulation of GPS using software signal generation and digital signal reconstruction [C]//Proceedings of the ION National Technical Meeting of the Institute of Navigation, 2000: 646-652.[4]Lee D U, Luk W, Villasenor J D, et al. A Gaussian noise generator for hardware based simulations [J]. IEEE Transactions on Computers, 2004, 53(12): 1523-1534.

[5]陈鹏飞, 孙克文, 杨东凯. 基于FPGA的GLONASS中频信号模拟器设计[J]. 全球定位系统, 2015, 40(2): 81-87.CHEN Pengfei, SUN Kewen, YANG Dongkai. GLONASS IF signal simulator design based on FPGA [J]. GNSS World of China, 2015, 40(2): 81-87. (in Chinese)

[6]Li D, Yue F H, Sun L S, et al. Study on GNSS satellite signal simulator [J]. Journal of Measurement Science and Instrumentation, 2013, 4(4): 349-352.

[7]孙国良, 沈士团, 丁子明, 等. 一种无源双星与多普勒导航系统组合的实现方法[J]. 航空学报, 2006, 27(4): 682-686.

SUN Guoliang, SHEN Shituan, DING Ziming, et al. An integration method for passive RDSS and DNS [J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(4): 682-686. (in Chinese)

[8]张硕, 寇艳红. GNSS模拟器中频调制卡设计与实现[J]. 北京航空航天大学学报, 2009, 35(5): 555-558.

ZHANG Shuo, KOU Yanhong. Design and implementation of IF signal modulator for GNSS signal simulator [J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(5): 555-558. (in Chinese)

[9]徐琪, 段哲民. 泰勒级数的DDS设计与FPGA实现[J]. 计算机工程与应用, 2014, 50(5): 208-211.

XU Qi, DUAN Zhemin.Design of DDS based on Taylor series and implementation in FPGA [J]. Computer Engineering and Applications, 2014, 50(5): 208-211.(in Chinese)

[10]齐巍, 常青, 张其善, 等. 高动态信号模拟器中的多普勒模拟算法[J]. 航空学报, 2008, 29(5): 1252-1257.

QI Wei, CHANG Qing, ZHANG Qishan, et al. Arithmetic of Doppler simulation in high dynamic signal simulator [J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1252-1257. (in Chinese)

[11]刘芊岑, 裘正定, 沈超. 高动态下三阶信号源的设计与实现 [J]. 计算机技术与发展, 2008， 18(5): 197-199.

LIU Qiancen, QIU Zhengding, SHEN Chao. Simulation and design of third-order high dynamics signal source [J]. Computer Technology and Development, 2008， 18(5): 197-199. (in Chinese)

[12]Zhang B, Liu G B, Jiao W, et al. High-order DDFS applied in simulated high-dynamic GNSS signal synthesis[C]//Proceedings of 9th International Conference on Electronic Measurement & Instruments, 2009, 4: 102-106 .[13]陈景润, 黎鉴愚. 关于自然数前n项幂的和[J]. 厦门大学学报(自然科学版), 1984, 23(2): 134-147.

CHEN Jingrun, LI Jianyu. On the sum of powers of natural numbers [J]. Journal of Xiamen University (Natural Science), 1984, 23(2): 134-147. (in Chinese)

Design of any-order direct digital synthesizer for high-dynamic GNSS signal Doppler simulation

ZHOU Chao, WANG Yueke, QIAO Chunjie, DAI Weihua

(College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China)

Abstract：In order to accurately simulate the Doppler characteristics of high dynamic GNSS signals, a method for designing any-order DDS (direct digital synthesis) signal synthesizer was proposed. An any-order DDS synthesizer structure was designed; a formula for calculating the initial phase of every accumulator in DDS synthesizer was derived by using theoretical analysis; a technique to determine the DDS word length was developed. Finally, the simulation accuracy of the proposed method for the Doppler characteristics of GNSS signals was validated through simulations. In addition, since the proposed method for designing DDS synthesizer has no order limitation, it can be widely used in different types of signal simulators.

Key words：high dynamic; GNSS signal; Doppler; any-order direct digital synthesis

doi:10.11887/j.cn.201603002

收稿日期：2016-01-18

基金项目：国家自然科学基金资助项目(61201031)

作者简介：周超(1988—)，男，贵州贵阳人，博士研究生，E-mail：zhouchaowhu@126.com； 王跃科(通信作者)，男，教授，博士,博士生导师，E-mail：wangyueke@139.com

中图分类号：TN967.1

文献标志码：A

文章编号：1001-2486(2016)03-007-05

http://journal.nudt.edu.cn