一类非线性生化系统的参数辨识

徐恭贤，刘　丰，王佳星

(渤海大学 数理学院， 辽宁 锦州 121013)



一类非线性生化系统的参数辨识

徐恭贤*，刘丰，王佳星

(渤海大学 数理学院， 辽宁 锦州 121013)

摘要：研究了一类非线性生化系统的参数辨识问题.针对一类非线性生化系统，建立了以浓度误差与斜率误差之和为目标函数的参数辨识优化模型.采用三次样条插值方法估计实验数据导数，运用MATLAB软件求解所建立的参数辨识优化模型.计算结果表明本文方法是有效的.

关键词：三次样条插值；参数辨识；生化系统

0引言

针对非线性生化系统的参数辨识问题，国内外学者已经做了很多有价值的研究工作〔1-9〕.例如，Liu和Wang〔1，2〕应用多目标优化方法求解S-型生化系统的参数辨识问题；Chemmangattuvalappil等〔3〕采用整数规划方法研究了非线性S-型生化系统模型的参数辨识问题；Vilela等〔4〕基于蒙特卡洛技术研究了S-型生化系统的参数辨识问题；Wu等〔5〕提出了一种蟑螂遗传算法用于S-型生化系统的参数辨识问题；为了解决参数辨识问题中求解S-系统微分方程计算量大和误差大等问题，Kimura等〔6〕运用分解法把原问题分解成若干子问题，然后对子问题进行分析求解；为了进一步解决计算量大和误差大的问题，Tsai等〔7〕利用修正配置法将微分方程转化成代数方程，再运用混合差分算法进行参数辨识.

本文针对非线性S-型生化系统，首先建立了以浓度误差与斜率误差之和为目标函数的参数辨识优化模型；然后采用三次样条插值方法估计实验数据导数，并运用MATLAB软件求解所建立的参数辨识优化模型.数值计算结果表明本文方法是有效的.

1参数辨识模型

考虑如下生化系统：

(1)

其中，X=(X1,X2,…Xn+m)T∈Rn+m;Xi(i=1,…,n)为生化系统的代谢物浓度；Xj(j=n+1,…,n+m)为生化系统的酶活性；αi和βi为速率常数；gij和hij为动力阶；向量p=(αT,βT,GT,HT)T，这里α，β，G和H可分别表示为：

α=(α1,α2,…，αn)T

(2)

β=(β1,β2,…，βn)T

(3)

gi=(gi1,gi2,…,gi(n+m))T,i=1,…，n

(4)

(5)

hi=(hi1,hi2,…，hi(n+m))T，i=1,…，n

(6)

(7)

为了确定模型(1)中的速率常数和动力阶，本文综合考虑浓度误差和斜率误差准则，建立了如下参数辨识优化模型：

(8)

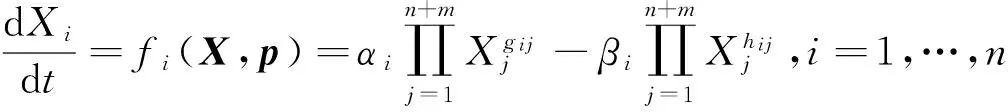
(9)

(10)

(11)

(12)

(13)

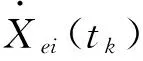
2参数辨识问题的求解

Xi(tk)=Xei(tk-1)+0.5ηk(fi(Xe(tk),p)+fi(Xe(tk-1),p)),i=1,…,n,k=1,…,NS

(14)

其中ηk=tk-tk-1.

则优化问题(8-13)可转化为如下非线性规划问题：

(15)

s.t.Xi(tk)=Xei(tk-1)+0.5ηk(fi(Xe(tk),p)+fi(Xe(tk-1),p)),i=1,…，n,k=1,…，NS

(16)

(17)

(18)

(19)

(20)

应用MATLAB软件提供的优化工具箱可以求解优化问题(15-20).

3数值算例

例1考虑如下生化系统〔11〕：

(21)

(22)

(23)

(24)

(25)

由式(8-13)可得生化系统(21-25)的参数辨识模型为：

(26)

(27)

(28)

(29)

(30)

(31)

0≤αi≤20,i=1,2,3,4,5

(32)

0≤βi≤20,i=1,2,3,4,5

(33)

-4≤gij≤4,i≠j,j=1,2,3,4,5

(34)

gij=0,i=j

(35)

-4≤hij≤4,i≠j

(36)

0≤hij≤4,i=j

(37)

取初值X(0)=(0.5,0.2,0.4,0.2,0.1,1,1,1,1)T，时间t的范围是0≤t≤0.5，时间间隔ηk=0.005，各参数的真实值如表1所示.

表2为无噪声情况下本文方法的参数辨识结果.由表1和表2可以看出，本文获得的参数辨识结果与真实参数值比较接近.为考察本文方法在有噪声情况下的性能，在代谢物浓度的实验值Xei(tk)中加入一个均值为零、标准方差为0.05Xei(tk)的高斯白噪声，参数辨识后生化系统的仿真曲线如图1所示.

表1参数的真实值

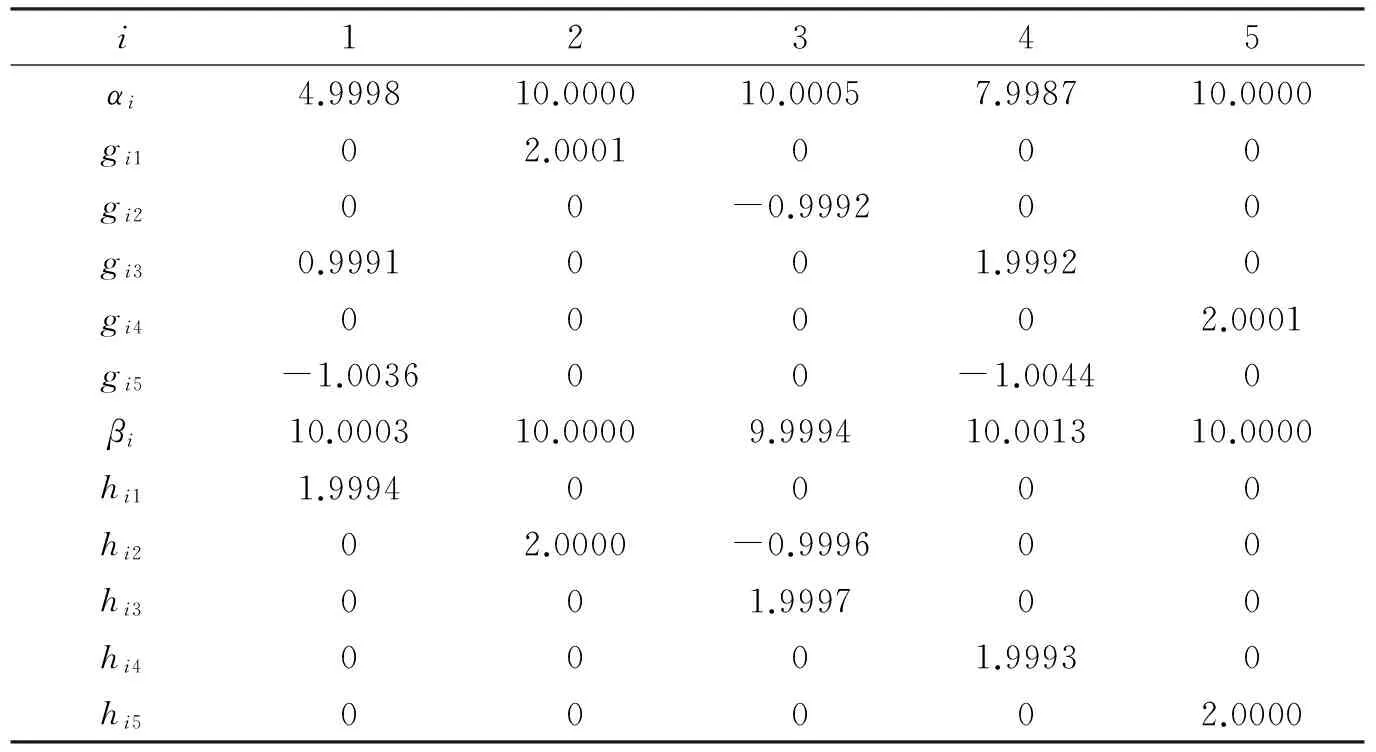
表2　无噪声情况下本文方法的辨识结果

4结论

针对一类非线性生化系统，本文建立了以浓度误差与斜率误差之和为目标函数的参数辨识优化模型，并为其设计了有效的求解方法.计算结果表明本文方法能够比较准确地辨识出生化系统的参数.

参考文献:

〔1〕LIUPK,WANGFS.InferenceofbiochemicalnetworkmodelsinS-systemusingmultiobjectiveoptimizationapproach〔J〕.Bioinformatics, 2008, 24(8): 1085-1092.

〔2〕LIUPK,WANGFS.Inverseproblemsofbiologicalsystemsusingmulti-objectiveoptimization〔J〕.JournaloftheChineseInstituteofChemicalEngineers, 2008, 39(5): 399-406.

〔3〕CHEMMANGATTUVALAPPILN,TASKK,BANERJEEI.Anintegeroptimizationalgorithmforrobustidentificationofnon-lineargeneregulatorynetworks〔J〕.BMCSystemsBiology, 2012, 3: 119.

〔4〕VILELAM,VINGAS,MAIAMAGM,etal.Identificationofneutralbiochemicalnetworkmodelsfromtimeseriesdata〔J〕.BMCSystemsBiology, 2009, 3: 47.

〔5〕WUSJ,WUCT.ComputationaloptimizationforS-typebiologicalsystems:Cockroachgeneticalgorithm〔J〕.MathematicalBiosciences, 2013, 245(2): 299-313.

〔6〕KIMURAS,IDEK,KASHIHARAA,etal.InferenceofS-systemmodelsofgeneticnetworksusingacooperativecoevolutionaryalgorithm〔J〕.Bioinformatics, 2005, 21(7): 1154-1163.

〔7〕TSAIKY,WANGFS.Evolutionaryoptimizationwithdatacollocationforreverseengineeringofbiologicalnetworks〔J〕.Bioinformatics, 2005, 21(7): 1180-1188.

〔8〕KIKUCHIS,TOMINAGAD,ARITAM,etal.DynamicmodelingofgeneticnetworksusinggeneticalgorithmandS-system〔J〕.Bioinformatics, 2003, 19(5): 643-650.

〔9〕KIMURAS,HATAKEYAMAM,KONAGAYAA.InferenceofS-systemmodelsofgeneticnetworksfromnoisytime-seriesdata〔J〕.Chem-BioInformaticsJournal, 2004, 4(1): 1-14.

〔10〕TheMathWorksInc.MATLAB[OL].http://www.mathworks.com/.

〔11〕HLAVACEKWS,SAVAGEAUMA.Rulesforcoupledexpressionofregulatorandeffectorgenesininduciblecircuits〔J〕.JournalofMolecularBiology, 1996, 255(1): 121-139.

Parameter identification for a class of nonlinear biochemical systems

XU Gong-xian，LIU Feng，WANG Jia-xing

(College of Mathematics and Physics，Bohai University，Jinzhou 121013，China)

Abstract：This paper addresses the parameter identification for a class of nonlinear biochemical systems. A parameter identification optimization model for these systems is established. This model can minimize the sum of least-square error and the slop error. A cubic spline interpolation method is used to estimate the derivatives of experiment data. The MATLAB software is applied to solve the proposed optimization model. The computational results show the effectiveness of the proposed approach.

Key words：cubic spline interpolation; parameter identification; biochemical systems

收稿日期：2016-01-18.

基金项目：国家自然科学基金项目(No: 11101051， No:11371071)；辽宁省高等学校优秀人才支持计划(No: LJQ2013115)；辽宁省自然科学基金(No: 2015020038)；辽宁省大学生创新创业训练计划项目(No: 201510167000012).

作者简介：徐恭贤(1976-)，男，博士，副教授，主要从事最优化方法与应用研究.

通讯作者：gxxu@bhu.edu.cn.

中图分类号：O29

文献标志码：A

文章编号：1673-0569(2016)01-0006-05