基于正交设计表的连续刚构桥主梁形状优化

2016-07-13许明

湖南交通科技 2016年2期

关键词：参数优化结构设计

许　明

(湖南尚上建设开发有限公司，湖南长沙　410022)

基于正交设计表的连续刚构桥主梁形状优化

许明

(湖南尚上建设开发有限公司，湖南长沙410022)

摘要：预应力混凝土连续刚构桥因结构整体性好，受力合理，施工方便而得到广泛应用。但在设计过程中，刚构桥主要参数的确定主要依靠设计经验，缺乏足够的理论依据。以国内外已修建的典型预应力混凝土连续刚构桥设计参数为依据，确定参数的合理取值范围，然后采用ANSYS建立参数化模型，基于正交表对某主跨200 m的连续刚构桥关键参数进行了优化研究。分析结果表明：基于ANSYS模型的正交试验设计法可快速、高效地得到较好的优化结果。对于该桥刚构桥优化后建议：边中跨比值为0.6，主跨与墩顶梁高比值为19，梁底曲线指数为1.8。

关键词：混凝土连续刚构桥；正交表；参数优化；结构设计

0引言

预应力混凝土连续刚构桥具有连续梁桥受力性能合理、行车平顺、施工方便等优点。连续钢构桥在200m以内具有足够的竞争力，虽然刚构桥的设计及施工经验均得到了有效积累，但是此类桥梁主要设计参数确定方式主要依靠经验，缺乏相应的理论基础[1-3]。

优化设计是结构设计的重要方向，它综合了计算力学、有限元理论、计算机学及规划学等多学科。优化设计按层次由低到高可分为：拓扑优化、结构形状优化、构件尺寸优化[4-6]。其中本文采用的构件尺寸优化是指在结构类型、材料参数、结构布局及几何构型已确定的情况下，对结构主要构件尺寸进行优化，常用的结构优化方法有规划法、遗传算法及准则法[7，8]。本文对混凝土连续刚构桥的优化主要是在结构形状优化的层次，并以现有规范的限制准则为基础，采用准则法对连续刚构桥进行结构参数优化。

1工程背景

研究的工程背景为某大跨高墩连续刚构桥。该桥为3跨预应力混凝土连续刚构箱梁桥。跨径组合为106 m+200 m+106 m=412 m，单幅桥宽度为12.5 m，主梁采用单箱单室结构，墩顶梁高12 m，跨中梁高3.5 m。图1为其墩顶及跨中箱梁尺寸图，材料为C55混凝土。汽车荷载为公路-I级。上部结构采用挂篮悬臂浇筑方式施工。

图1　断面图(单位： cm)

2有限元模型建立

计算模型如图2所示。边界条件为墩底固结，边跨支座采用竖向支承。有限元模型采用ANSYS软件参数化建模，选取需要优化的3个参数作为变量，分析模型的其他参数与边界条件和实际工程保持一致。

图2　计算模型参数示意

假定桥梁总长为L，边跨长L1，中跨长L2。边中跨长度比值为λ。如图2所示，假定薄壁墩高度为H，梁底曲线指数为n。

采用ANSYS内嵌的APDL语言建立参数化计算分析模型，其中箱梁及桥墩均采用shell63单元模拟，预应力钢束采用link10单元。通过ANSYS的生死单元模拟施工过程[9]，典型的APDL命令为Ekill、Ealive，有限元分析模型如图3。

图3　有限元分析模型

本次优化的设计参数为：边中跨比值λ、梁底曲线指数n，主跨与墩顶梁高比值k，常规模拟过程采用单变量参数模拟法，即保持3个参数3个不变，依次只改变其中的1个，这样不断循环分析，最后统计参数结果，得到一组最优参数，但是这种分析法效率较低，而且可能因参数设置不合理导致分析结果不收敛，因此在进行参数优化之前需进一步优化分析策略。本文采用的优化策略为： ①根据以往刚构桥设计经验统计设计参数的合理区间； ②基于正交试验设计涉及法，选用合适的正交表，安排计算项目。

3连续刚构桥设计参数统计分析

根据已建国、内外混凝土连续刚构桥[1-3]的设计参数，对刚构桥边中跨比值、梁底曲线指数、主跨与墩顶梁高比值(跨高比)等参数进行统计。确定分析参数的变化范围以便于参数优化。

经统计调查发现：混凝土连续刚构跨径布置通常采用不等跨形式。边中跨比值在0.5～0.7之间，图4为既有连续刚构桥边中跨比值的统计。统计发现：大跨连续刚构桥梁底曲线指数一般小于等于2，通常采用1.6次或1.8次抛物线，本文优化时梁底曲线指数的取值范围为1.5～2.0。

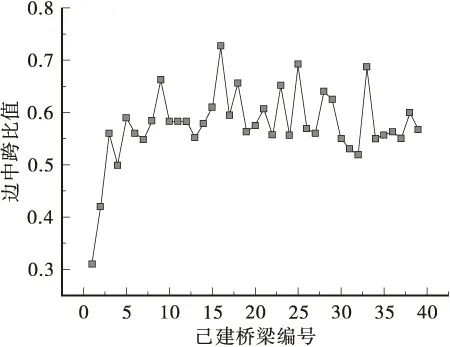
图4　已建连续刚构桥边中跨比值统计

图5a、5b分别为既有混凝土连续刚构桥主跨与根部梁高比值、主跨与跨中梁高比值的统计。统计结果表明：主跨与根部梁高比值在15～20之间，主跨与跨中梁高的比值在35～65之间。

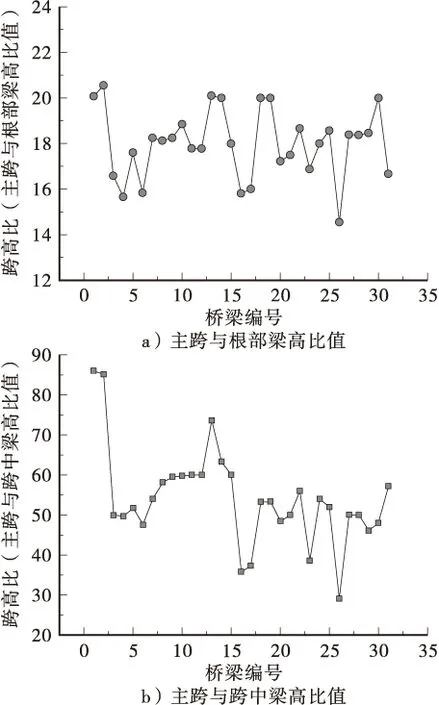
图5　混凝土连续刚构桥跨高比统计

基于既有桥梁统计结果，本文优化时，边中跨比值在0.5～0.7之间，梁底曲线指数的取值范围为1.5～2.0，主跨与根部梁高比值在15～20之间。

4优化设计方法

本文采用准则法进行参数优化，优化的关键是确定约束方程的确定、目标函数、正交试验的设计。

4.1确定约束函数

本文的约束条件为施工过程中的应力水平、运营阶段的应力状态及变形条件，如式(1)～式(3)所示。

施工阶段应力约束：

(1)

运营阶段应力约束：

(2)

运营阶段位移约束：

(3)

4.2确定目标函数

目标函数直接关系优化结果的可行性，是参数优化的关键步骤。对于本文的混凝土连续刚构桥，随着优化参数的改变，结构的内力大小及分布均将发生较大的改变，合理的分析结果应要满足在一定条件下材料强度得到最大程度的利用。为使所有选的截面应力的方差最小，构造目标函数f1：

(4)

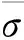
为使所选截面应力的均值最小，构造目标函数f2：

(5)

式(5)中：f2为第2个构造目标函数。通过第1和第2目标函数就可得到使截面应力最均匀的参数组合。在满足构件截面应力均匀的情况下，一般还希望尽量减少材料用量，因此引入目标函数f3：

f3=混凝土用量最小

(6)

因此本文的目标函数为3个，但实际分析中同时考虑多目标最优问题时，常常会导致多目标间相互冲突。于本文目标函数的特点选择采用评价函数法中的极小距离理想点法[10]。分析的步骤如下：

第1步：求个目标函数的理想点。对3个目标函数分别求最小，如式(7)所示。

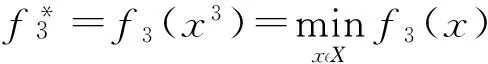
(7)

第2步：检验理想点。若理想点为绝对最优点，即若x1=x2=x3，则输出最优解x*=x1(x2或x3)，若理想点不是绝对最优点，则进行第3步。

第3步：求极小距离，按式(8)求解多目标函数的极小距离：

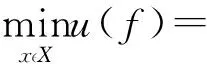
(8)

4.3正交试验表设计

由于本文优化模型需考虑到3个因数，每个因数的变化范围又有3～6项，因此实验次数较多，因此选择通过正交试验表选择一部分有代表性水平组合进行试验[11]。由于各个因素的水平数不同，本文采用混合正交表进行分析。各个因素水平取值依据统计结果确定。各因素的水平选择如表1所示。表1中：因素1至因素3分别为：边中跨比、主跨与根部梁高比值、梁底曲线指数。边中跨比、跨高比均考虑6个水平度，梁底曲线考虑3个水平度。

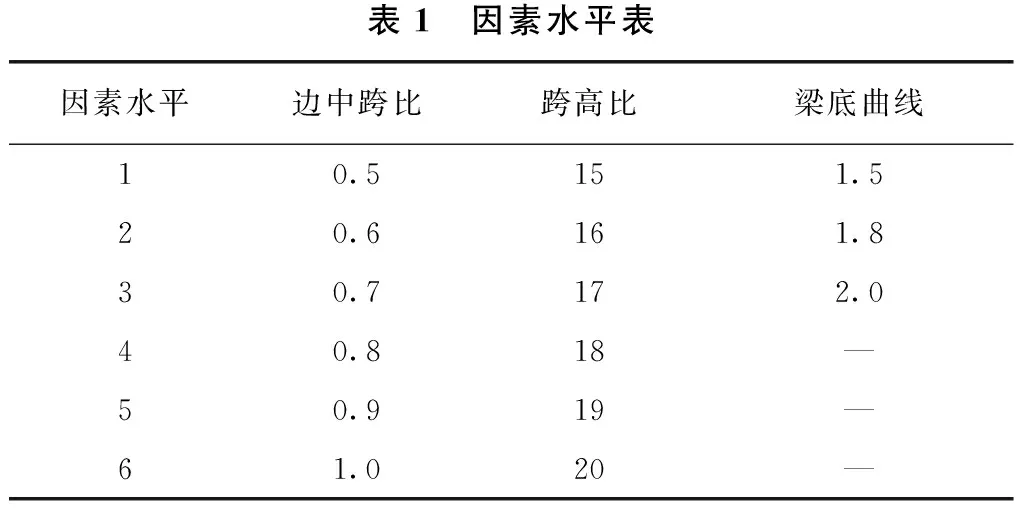
表1 因素水平表因素水平边中跨比跨高比梁底曲线10.5151.520.6161.830.7172.040.818—50.919—61.020—

5优化分析结果

表2 正交表计算结果试验号边中跨比跨高比梁底曲线多目标10.5171.50.9020.5151.80.8630.5162.00.8240.5192.00.7450.5201.80.8260.5181.50.84

表3 正交表多目标分析结果试验号边中跨比跨高比梁底曲线M14.905.099.99M24.885.009.99M34.945.009.70M44.925.000.00M54.954.890.00M64.924.960.00R0.080.200.28

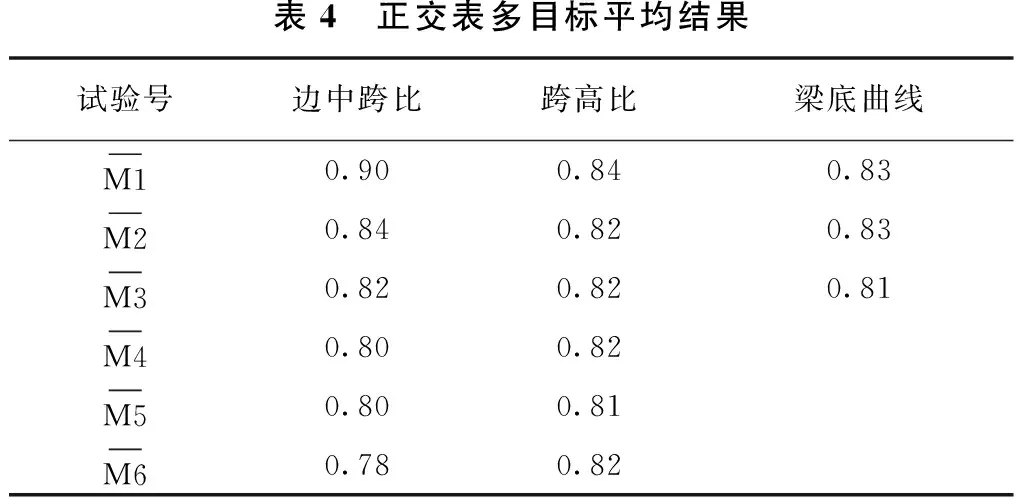
表4 正交表多目标平均结果试验号边中跨比跨高比梁底曲线M10.900.840.83M20.840.820.83M30.820.820.81M40.800.82M50.800.81M60.780.82

其中各水平多目标总和的数值最小的为最好的水平，比较分析结果表3中各列的各水平多目标总和的数值可以发现，对于边中跨比值这一因素，比较M1～M6的大小，发现M2最小，于是相应的0.6是使目标函数最优的边中跨比值。同理可得其他各因数的最优选择。基于分析结果得到，该连续刚构桥的最优组合参数为：边中跨比值为0.6，主跨与墩顶梁高比值为19，梁底曲线指数为1.8。

6主要结论

1) 采用大型有限元软件ANSYS建立参数化模型，结合正交试验法对某大跨高墩连续刚构桥进行优化设计，分析结果表明：基于ANSYS模型的正交试验设计法可快速高效地得到较好的优化结果。

2) 基于统计结果，混凝土连续刚构桥边中跨比值在0.5～0.7之间，梁底曲线指数的取值范围为1.5～2.0，主跨与根部梁高比值在15～20之间。

3) 利用正交试验的方法进行结构的优化，并得到了一组优化参数。建议：边中跨比值为0.6，主跨与墩顶梁高比值为19，梁底曲线指数为1.8。

参考文献：

[1] 保林.高墩大跨连续刚构桥[M].北京：人民交通出版社，2001.

[2] 周军生，楼庄鸿.大跨径预应力混凝土连续刚构桥的现状和发展趋势[J].中国公路学报，2000，13(1)：31-37.

[3] 杨高中.连续刚构桥在我国的应用和发展[J].公路，1998(6)：1-7.

[4] 李明燕，方志.预应力混凝土连续刚构桥的参数优化[J].公路工程，2008，33(1)：74-80.

[5] 胡雄伟.大跨连续刚构桥主梁设计参数的优化研究[D].昆明：昆明理工大学，2008.

[6] 李杰，徐岳，郑凯锋.预应力混凝土连续刚构桥结构参数分析[J].广西交通科技，2003，28(5)：28-30.

[7] 李杰.大跨径 PC 连续刚构桥设计参数优化研究[D].西安：长安大学，2003.