内灌砂钢管柱受力性能有限元分析

徐　鑫， 陈建兵， 俞志豪

(苏州科技大学 土木工程学院， 江苏 苏州　215011)



内灌砂钢管柱受力性能有限元分析

徐鑫， 陈建兵， 俞志豪

(苏州科技大学 土木工程学院， 江苏 苏州215011)

摘要：内灌砂钢管柱是目前桥梁施工中常用的一种临时支撑结构，为研究其受力特征，采用ABAQUS软件建立其不同构造参数的有限元模型。经模拟计算分析，得到了轴心荷载作用下各模型的极限承载能力，对比了钢管柱、混凝土钢管柱与内灌砂钢管柱的荷载-位移曲线、荷载-应变曲线变化规律。在内灌砂密实度相同情况下，讨论了长细比、径厚比、含钢率等3参数对内灌砂钢管柱的纵向位移和纵向应变的影响，且其承载力随三者变化也较为显著。该研究结果对内灌砂钢管柱在桥梁施工中的推广应用提供了参考。

关键词：内灌砂钢管柱； 受力性能； 轴心受压； 有限元； 承载力

0引言

随着国民经济的高速发展，各类重大工程、建设项目包括大跨度空间结构、高层结构也日益增多。为了满足这些大型结构的施工顺利进行和施工质量的保证，需要搭设稳定的临时结构来辅助施工。当前常用的临时支撑可分为整体式稳定体系、半稳定体系、单点支撑体系三种类型[1]。在施工中由于钢管柱单点支撑安装简单、施工成本少、并可周转使用等特点，所以在工程施工较为常见，且备受工程界青睐[2]。

在钢管中灌入砂子而形成的支撑柱，由于其承载能力、稳定性等特性皆较空心钢管支撑优越，近几年来，工程界已对其进行相关应用及研究。如文献[3]把内灌砂钢管柱作为钢筋混凝土桩的接长支架结构、文献[4]把灌砂钢管柱成功应用于基坑围护中、文献[5]研究了砂卵石的不同压实度对内灌砂卵石方薄壁钢管柱承载力性能的影响。但内灌砂钢管柱独立作为支撑结构，例如如图1所示，还鲜见有相关研究报道。因而，有必要对其受力性能进行研究。

图1　某桥梁内灌砂钢管临时支撑柱

本文采用ABAQUS有限元软件建立了砂钢管柱的结构模型，通过对其长细比、径厚比、含钢率等参数研究，分析了其对砂钢管柱受力性能的影响。

1构件设计

参照图1中内灌砂钢管支撑柱的实际尺寸进行缩尺，设计了直径分别为89、108、133 mm 等3种不同长细比的内灌砂钢管柱，钢管皆采用强度等级为Q235的钢。为对比其受力性能，又分别设计了1根钢管柱和内灌C20混凝土的钢管混凝土柱。构件设计参数见表1所示。在表1中，SFST表示钢管砂；CFST表示钢管混凝土；ST表示空心钢管；D为钢管外直径；L为试件长度；λ为长细比；α为含钢率。

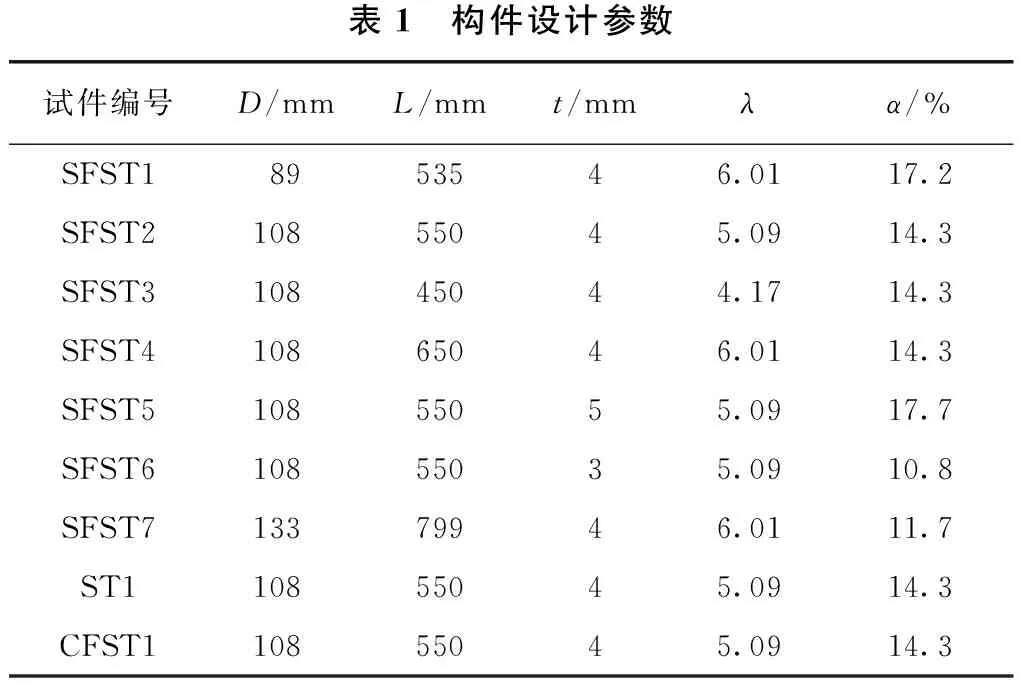
表1 构件设计参数试件编号D/mmL/mmt/mmλα/%SFST18953546.0117.2SFST210855045.0914.3SFST310845044.1714.3SFST410865046.0114.3SFST510855055.0917.7SFST610855035.0910.8SFST713379946.0111.7ST110855045.0914.3CFST110855045.0914.3

2模型建立

2.1组建构件

根据表1中的构件设计参数，建模时内灌砂钢管柱采用全截面形式，并在柱上下端各设置尺寸为170 mm×170 mm×10 mm的刚度无穷大的垫块作为加载板。底垫块板采用固定端约束，顶垫块板约束X和Y方向自由度。其组成结构如图2所示。

图2　支撑柱组成结构(单位： mm)

2.2材料本构模型

应力-应变关系是工程结构受力过程中材料受力和变形关系的概括，是内部微观机理的宏观表现。对应力-应变关系模型准确的确立关系到有限元软件模拟的准确性，以下依次对钢材、混凝土、砂子的本构模型参数进行确定。

2.2.1钢材本构模型

钢材本构模型选取双直线模型[6]，其应力-应变关系为：

(1)

式中：σ为钢材等效应力；取fu=1.5 fs；钢管的弹性模量为Es=2.1×105MPa；εi为钢管的等效应变；εy为钢管屈服时应变；εst为钢管强化时的应变；εu为钢管达到极限强度时的应变，取εst=12εy，εu=120εy，ζ=1/216。

2.2.2混凝土本构模型

混凝土本构关系模型采用ABAQUS中自带的混凝土损伤塑性模型，其受压应力-应变关系模型参数取值参考文献[6]。具体表达式如下：

(2)

2.2.3砂子本构模型

ABAQUS中拓展的Drucker-Prager模型根据屈服面在子午面上的形状分为3种：线性D-P模型，双曲线D-P模型和指数型D-P模型。文中砂子本构采用线性D-P模型，该模型是目前为止岩土工程方面运用十分广泛的本构模型，可以很好地反映岩土非线性变形的特点[7，8]。

线性Drucker-Prager模型的屈服函数为[8]：

F=t-ptanβ-d=0

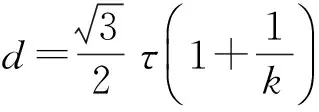
2.3加载方法

在有限元求解过程中考虑相关非线性因素，采用位移增量迭代法加载的方式施加荷载，利用Amplitudes方法建立加载规律，将位移加在轴心RP1点与上垫块的耦合处。进而利用位移反算荷载以得到荷载-位移曲线、荷载-应变曲线。

2.4有限单元划分及界面的处理

圆钢管砂中的钢管采用4节点壳单元(S4R)，砂和混凝土以及刚性加载板均采用8节点三维实体单元(C3D8R)，该种单元类型计算精度比较低，但计算自由度可以减少很多，从而加快有限元软件计算速度。整个模型采用六面体结构化网格划分，在进行网格划分的时候，根据计算精度要求，对钢管、砂子、混凝土进行精细化划分，加载板则粗略划分。网格划分见图3所示。

　a) 有限元模型　　b) 加载板刚体　　c) 砂实体单元　　d) 钢管壳单元　

为考虑受压过程中钢管和砂协同受力，本文定义加载板与内灌砂为绑定约束，加载板和钢管端采用壳实体耦合，钢管和砂之间定义库伦摩擦，具体参数参见文献[7]，该模型有法向接触和切向黏结构成。

3计算结果分析

ABAQUS模拟计算所得到的各个模型极限承载力及纵向位移的计算值，其中CFST1柱抗压承载能力为791.43 kN，约为SFST2柱承载力的1.32倍，SFST2柱的峰值荷载相比与ST1柱提高了约35%左右。不同长细比、径厚比、含钢率砂柱的极限承载力也有所不同，但较纯钢管柱都有所提高，见表2所示。

3.1灌砂柱受力特征

这里仅以模型SFST2为例进行内灌砂钢管柱的受力分析，其在轴心压力下的变形及云应力分布如图4所示。

在模拟计算过程中，当加载接近极限荷载600 kN时，受压柱两端发生局部屈曲，压力稍微增加模型呈现出破坏现象，表明其已丧失承载能力。从图4b、图4c可以看出钢管和砂子整体压应力分布均匀，但在荷载作用下钢管首先受力，之后内灌注砂即协同钢管共同受力。由于钢管的约束效应，靠近钢管外围的砂子首先出现了屈服，其应力明显大于管内近圆心砂子。

表2 各模型参数模拟值试件编号Δ/mmNu/kNμ1SFST12.5574.981.23SFST22.56600.781.29SFST32.56680.121.45SFST42.54557.811.19SFST52.52654.471.4SFST62.52554.471.19SFST72.5399.970.86ST12.49467.481CFST12.62791.431.69 注:Δ为纵向位移;Nu为极限承载力;μ1为各试件的极限承载力与试件ST1承载力之比。

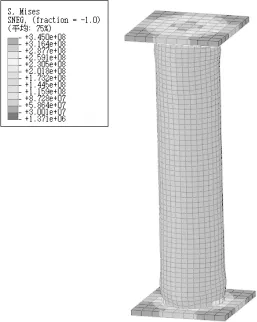
　a) 整体变形图　　b) 钢管云应力　　c) 砂柱云应力　

3.2荷载-纵变形曲线

图5给出了CFST1和ST1与基本模型SFST2的荷载-纵向变形对比曲线。从图中曲线变化可以看出，CFST1柱在弹性阶段荷载上升比较快，说明在开始阶段就具有较高的刚度，进入屈服阶段后纵向位移逐渐增大。ST1和SFST2在弹性阶段曲线几乎重合，随后ST1先开始出现屈服，SFST2柱仍继续上升，其峰值点荷载较ST1明显提升。3种模型的峰值荷载对应的纵向位移基本相同，在加载后期钢管砂柱荷载值略微下降，曲线下降段较小而钢管混凝土柱和纯钢管柱则无明显下降段。

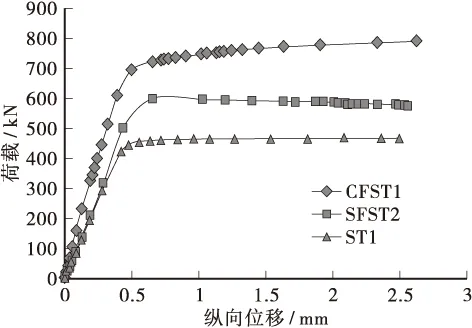
图5　荷载-纵变形曲线

3.3荷载-纵应变曲线

模型CFST1、ST1、SFST2的荷载-纵向应变曲线如图6所示，可以看出在相同条件下钢管混凝土柱的应变延性最好，相比于钢管柱，砂管柱具有较好的抵抗变形能力，其纵向应变约为钢管柱的2倍左右。可以这么认为，具有一定压实度的内灌砂钢管柱可以增强钢管柱的自生稳定性，从而保证构件具有更高的承载能力。

图6　荷载-纵应变曲线

3.4结构参数对灌砂柱的影响

3.4.1长细比

图7为不同长细比λ的钢管砂柱的荷载-纵向位移曲线、荷载-应变曲线。从中可以看出，长细比λ=4.17的SFST3荷载曲线上升最快，峰值荷载达到700 kN左右，而后逐渐略微有所下降。当长细比由4增加到6时，承载力下降了约19%。这是由于随着长细比的增大，构件开始由短柱向长柱发展，承载力会逐渐减小，因而长细比为4左右的钢管砂具有最大承载力。随着λ的增加荷载-应变曲线也开始下降，构件的后期延性略有降低，如图7b所示。

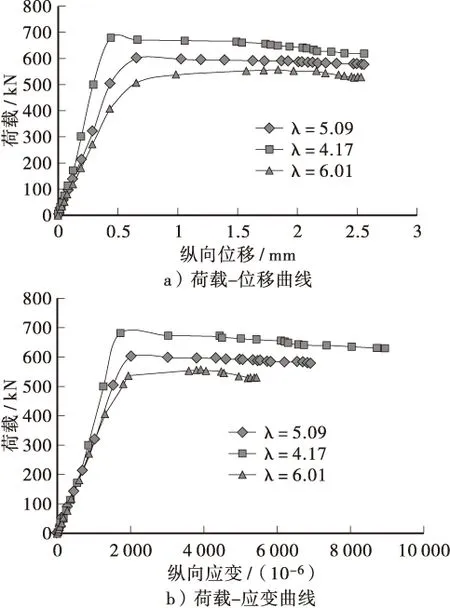
图7　不同长细比影响

3.4.2径厚比

图8a所示，在其它条件相同的情况下，SFST2、SFST5、SFST6灌砂柱的荷载-位移曲线的弹性阶段几乎重合，表明这三类砂柱具有相近的初始刚度。随着管壁的厚度(径厚比)增加，构件的极限承载能力也有所提高，如t=5 mm(径厚比为21.6)比t=3(径厚比为36)的构件提高约20%，但荷载后期纵向位移变化则基本一致，可以说明具有相近的延性。图8b可以看出，这些构件达到峰值荷载时对应的纵向应变基本差不多，相比于厚度小的钢管砂柱，厚度大的具有更高的抵抗变形能力。

图8　不同径厚比影响

3.4.3含钢率

含钢率对构件的承载力也很大，如图9所示，不同含钢率α变化范围为11.7%～17.2%时的3种构件的荷载-位移曲线、荷载-应变曲线。结果表明，在其他条件相同的情况下，构件SFST1较SFST7的α的增加了47%，其承载值提高了70%左右。图9b结果表明，随着α的变化，纵向应变也相应的提高，但在后期荷载中不为明显。

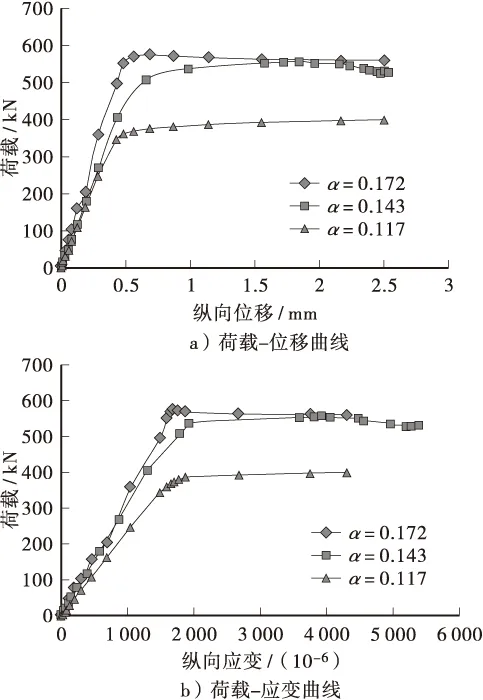
图9　不同含钢率影响

4结论

1) 在轴心受压作用力下，具有一定压实度的灌砂钢管柱由于砂和圆钢管共同作用，一定程度上延缓了圆钢管柱的屈曲，改善钢管柱的整体稳定性。相比于钢管柱，灌砂钢管柱的轴心抗压承载能力提高了约35%左右。相对于钢管混凝土柱，这种新型的灌砂钢管柱临时支撑可以重复利用原料，具有经济性和环保性的特点。

2) 长细比不同的钢管砂柱，在轴心受压作用力下，长细比为4的构件具有最高的承载力，随着长细比的增加，极限承载力随之下降，各构件的荷载位移、荷载应变形状基本相似。长细比变化对构件的极限承载力较为明显。

3) 径厚比和含钢率对钢管砂柱的承载能力有一定的影响，尤其是含钢率的变化更为明显。含钢率提升6%左右，其钢管砂柱的极限承载能力提高了70%左右。

参考文献：

[1] 秦海强，靳军峰，辛森.临时支撑在场馆类大型钢结构安装中的应用[A].第十届中国科协年会论文集(四)[C].2008.

[2] 余流.施工临时结构设计与应用[M].北京：中国建筑工业出版社，2010.

[3] 郦铃福.钢管砂桩在深水无覆盖层支架现浇上部结构中的应用[J].中国公路学报，1995，8(4)：64-70.

[4] 周成，蔡整银，殷建华.大型深基坑中钢筋混凝土联合钢管砂支撑的应用与快速拆除[J].华南理工大学学报，2003，31(S)：56-62.

[5] 刘欢，姚勇，褚云朋，等.内填砂卵石薄壁方钢管柱轴压性能试验研究[J].工业建筑，2013，43(9)：120-123.

[6] 丁发兴，周林超，余志武，等.钢管高性能混凝土短柱受力性能研究[J].建筑结构学报，2002，23(2)：41-47.

[7] 江涛.大直径超长钻孔灌注桩群桩效应的三维非线性有限元分析[D].南京：河海大学，2007.

[8] 刘世涛，程培峰.基于ABAQUS土体数值分析的本构模型[J].低温建筑技术，2010(2)：90-92.

文章编号：1008-844X(2016)02-0165-05

收稿日期:2016-01-07

作者简介:徐鑫( 1991-) ，男，硕士研究生，主要从事桥梁结构的研究

通讯作者:陈建兵( 1968-) ，男，教授，主要从事桥梁结构的研究。

中图分类号：U 445

文献标识码：A