“CAT初始作答影响最终成绩”的模拟分析与纠正*

简小珠，戴海琦

(1.上饶师范学院教育科学学院，上饶 334001；2.江西师范大学心理学院，江西省心理与认知科学重点实验室，南昌 330022)



“CAT初始作答影响最终成绩”的模拟分析与纠正*

简小珠1，2，戴海琦2

(1.上饶师范学院教育科学学院，上饶 334001；2.江西师范大学心理学院，江西省心理与认知科学重点实验室，南昌 330022)

摘要：在两参数模型(2PM)下模拟计算机化自适应测验(CAT)初始阶段的三种作答情境，由模拟结果发现只有当被试作答情境为睡眠现象时会导致能力低估现象，猜测现象时会导致能力高估现象，并探讨了“CAT初始阶段作答影响最终成绩”考试现象发生的具体情境范围。由模拟结果分析可得，CAT考试现象是被试作答异常现象(猜测、睡眠现象)和CAT数学模型(2PM)共同影响的结果。在四参数模型(4PM)、2PM-Biweight下进行CAT模拟，被试能力高估现象和低估现象都得到了较好的纠正。

关键词：CAT；CAT模拟；猜测现象；睡眠现象；能力高估；能力低估

1研究背景

1.1“CAT初始作答影响最终成绩”考试现象及以往的研究

许多参加过CAT测试的被试有这样的体验：如果初始阶段的几道试题都答对了，即使测验后期阶段答错了若干道难度较大的试题，仍可能得到较高的分数；如果在初始阶段的几道试题有些答错了，即使后期阶段被试做得很好，也难以得到高分。所以有这样的说法，“千错万错，头五道试题不能错”(张华华，程莹，2005)。本文将这种现象命名为“CAT初始作答影响最终成绩”考试现象，简写为CAT考试现象。在CAT实践中也存在着被试能力低估事件，张华华(2002)论述到ETS曾经让参加GRE-CAT测试大约0.5%的被试免费重考，许多研究者认为由于这些被试能力估计值过低；在商学院研究生入学考试中曾有将近一千人的被试的分数估计不准确(Merritt，2003)。

已有研究者从选题策略、数学模型的角度来纠正CAT考试现象。张华华(2002)认为是CAT的选题策略存在设计误区所导致被试能力低估，并通过公式推导论述，强调a参数导致被试最终能力估计偏差过大。Chang和Ying(2008)在CAT模拟中使用a分层信息量方法，在测验开始时选择区分度较小的试题，可以在一定程度上避免被试能力被低估。Rulison 和Loken(2009)在三参数模型下进行CAT模拟，发现高能力被试(即得分前10%的被试)答错前两题会存在能力低估现象；在四参数模型下高能力被试不再出现能力低估现象。Yen，Ho，Laio，Chen和Kuo(2012)在CAT实例研究中使用四参数模型时，发现高能力被试答错前两题而没有出现能力低估现象。但Rulison，Loken，Yen等以往研究中还有以下几个方面没有进行探讨：(1)没有对CAT中被试能力高估现象进行模拟分析，也没有探讨对CAT高估现象的纠正方法；(2)在数学模型上只有三、四参数模型的设计，没有两参数模型；本文认为，在实际使用中多数是两参数模型，Rasch模型(也可以看作是两参数模型的一个特例)，而且在两、三、四参数模型下进行比较，才能更为完整的分析被试能力低估与高估现象的发生情况以及对应的纠正情况；(3)没有确切探讨和回答CAT考试现象产生的具体发生情境范围，即在什么样的情境或在什么样的情境下会发生被试能力高估现象或低估现象；也没有探讨纠正方法(4PM)对能力低估和高估现象纠正的发生范围。本文将对以上几个方面进行探讨。

Mislevy和Bock(1982)在纸笔测验时使用2PM-Biweight方法实现了对被试能力的稳健性估计。2PM-Biweight是在2PM下对极大似然估计方法的改进，本质上是2PM的改进形式，本文简写为2PM-BIW。BILOG软件中有Biweight方法命令。简小珠，戴海崎，彭春妹(2007)在固定纸笔测验形式下使用四参数模型能纠正被试能力高估和低估现象。以上两个研究都是纸笔测验形式，而在CAT测验时四参数模型、2PM-BIW是否能纠正被试能力高估和低估现象，这是本文将要探讨的内容之一。

1.2本文的研究思路

本文将从猜测现象和睡眠现象的角度对CAT考试现象进行探讨。Mislevy和Bock(1982)认为被试只有试题难度远远大于被试能力时(即期望概率P小于0.20)才会进行猜测，并将猜测作答的临界期望概率分为0.15，0.10，0.05三种水平。期望概率计算是根据被试能力水平(需已知)和项目参数(需已知)而计算出来的概率。本文将在2PM下期望概率P小于0.05时被试在高难度试题上得分的现象命名为猜测现象。高能力被试由于焦虑、转录错误、动机过强等原因可能导致答错相对容易的试题，Wright(1977)称为睡眠现象。本文将在2PM下期望概率P大于0.95时被试在相对容易的试题失分的现象命名为睡眠现象。这里将能力区间为[-1.64，-3]的被试定义为低能力被试，约占正态分布群体的5%，区间为[1.64，3]的被试定义为高能力被试，约占5%。本文假设：(1)如果高能力被试在初始阶段连续答错多道中等难度试题，且期望概率P>0.95(睡眠现象)则可能会出现能力低估现象；(2)如果低能力被试在初始阶段连续答对多道中等难度试题，且P<0.05(猜测现象)则可能会出现能力高估现象。本文将在两、三、四参数模型下模拟CAT初始作答情境，分析被试能力高估和低估现象及其纠正。

2CAT模拟设计

CAT模拟测试使用两、三、四参数模型，和两参数模型的改进形式(2PM-BIW)。模拟题库1500题，log(a)服从正态分布N(0，1)，b参数服从U[-3，+3]。在三、四参数模型时，c参数固定为0，γ参数固定为1。

Bock & Mislevy(1982)从[-3，+3]选取31个能力水平的被试进行CAT模拟。Belov等(2008)，Chang和Ying(2008)在CAT模拟时在能力区间内选取有限个数的代表性样本点。同样本文选取-2.7，-2.4…2.4，2.7共19个代表性点的被试，每个被试模拟次数为5000次。能力真值为-2.7的被试模拟5000次，可以等同代表[-2.85，2.65]区间的50名被试模拟100次；能力真值为-2.4的被试，则代表[-2.65，2.35]，依此类推。

CAT初始阶段设计三种情境：(1)前两题正常作答；(2)答对前两题(第1题a=1.2，b=0，第2题a=1.2，b=0.3)；(3)答错前两题(第1题a=1.2，b=0，第2题a=1.2，b=-0.3)。从第3题开始从题库中选题，被试都按正常水平作答。如果在3PM时前两题c参数安排为0.20；在4PM时前两题的c参数为0.20，γ参数为0.98。被试按正常水平作答，是指根据被试能力真值θα与选择出来的试题计算概率P，再由随机函数生成一个随机数φ，比较P与φ来确定被试得分。

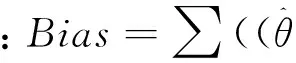
3结果与分析

(1)前两题正常作答时由表1可知，在四种模型(方法)下，各个能力水平被试的Bias都很小，在0.01以内，说明对每个被试能力估计都十分准确。在IRT和CAT的一些研究中，试卷难度和题库难度情况是处于难度量尺中间的题量多，处于难度量尺两端的题量少，因而会导致中间水平的被试估计准确性要高于两端的被试。而本文题库试题难度服从均匀分布U[-3，+3]，因此，在正常作答情况下所有被试能力被试的估计都具有同样的准确性，或模拟返真性。

(2)答对前两题时在2PM模型下，从1至19号被试的Bias逐渐增大，被试能力真值越小，Bias就越大。17号被试在前两题的期望概率分别为0.014，0.007，小于0.05，为猜测现象。17号被试的Bias为0.298，出现了能力相对高估现象。18、19号被试存在同样的能力高估现象。这种能力高估现象可以较好的解释CAT考试现象的能力高估现象发生的具体情境。而在1至10号被试之间的Bias相对都很小，这说明不是所有被试答对前两题都会形成能力高估现象。

而在BIW，3PM，4PM方法下，从1至14号被试与2PM模型下的情况相似，Bias逐渐增大。14号至19号被试的Bias逐渐减小。这也就是说，原来在2PM下的能力高现象，在3PM，4PM，BIW方法下得到有效纠正。而且，在3PM，4PM，BIW方法下的Bias值在13至15号被试之间发生了拐点，也就是说，当被试所答对前两题的难度大于被试能力估计值约0.9至1.5之间，3PM，4PM，BIW方法对被试能力估计值逐渐产生了纠正作用。

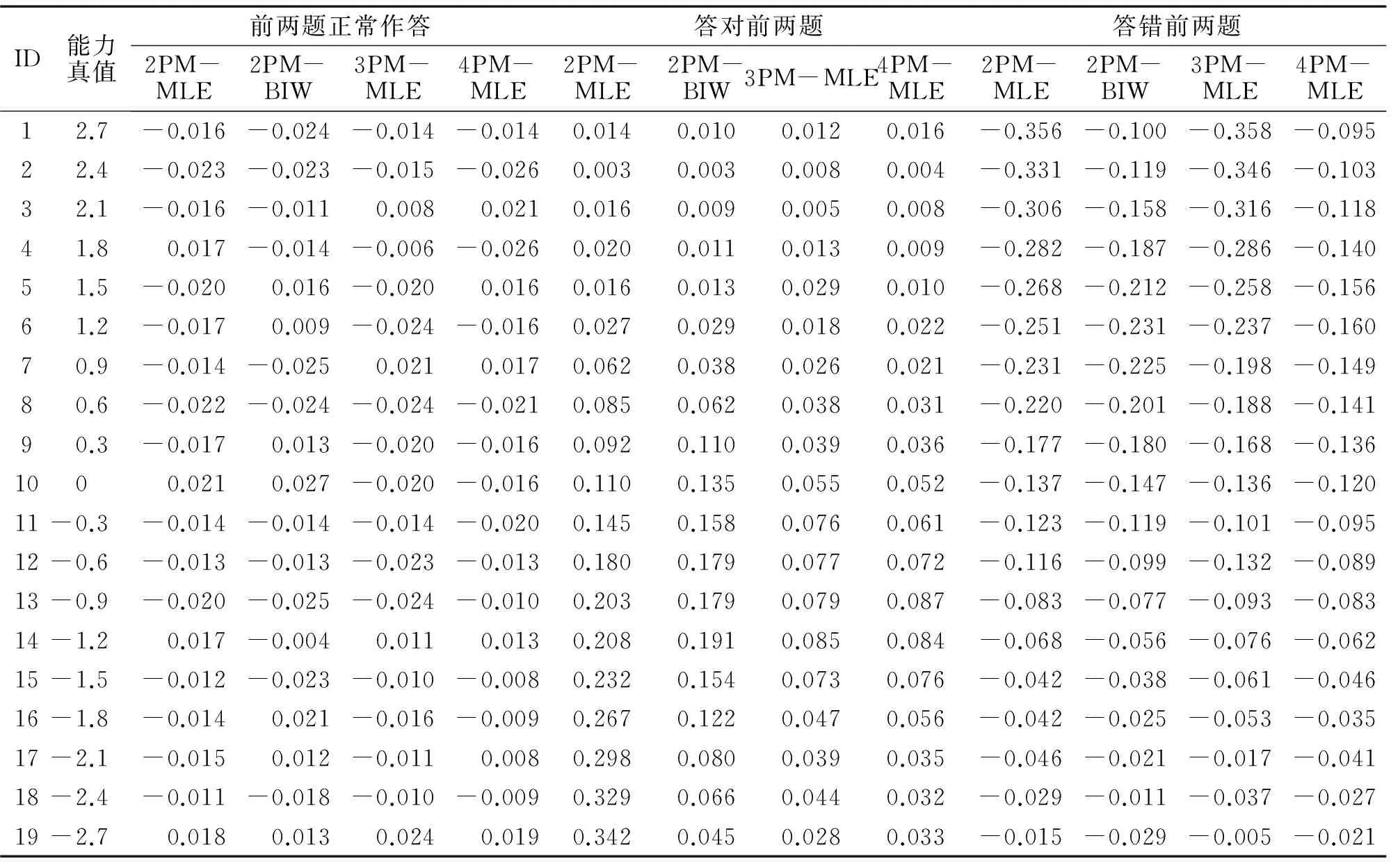
表1　CAT模拟结果

注：表中的加粗部分数据，处于2PM-BIW、3PM-MLE、4PM-MLE方法对能力高估和低估现象纠正的拐点区域的被试群体；表中的斜体，且加粗部分数据，处于2PM-BIW、3PM-MLE、4PM-MLE方法对能力高估和低估现象进行有效纠正区域的被试群体。如果再重复测验模拟5000次，表中的Bias值会在0.002左右幅度波动。

(3)答错前两题时在2PM，3PM模型下，从19至1号被试，随着被试能力水平增大，Bias的绝对值逐渐增大。3号被试在前两题的期望概率分别为0.973，0.983，期望概率大于0.95，而被试却答错了，属于睡眠现象。3号被试的Bias在2PM，3PM模型下为-0.306，-0.316；出现了能力相对低估现象。1、2号被试存在同样的能力低估现象。这种能力低估现象，这可以较好的解释了“CAT初始作答影响最终成绩”现象的能力低估现象。从19号至10号被试之间的Bias相对都很小，这说明不是所有被试答错前两题都会形成能力低估现象。

在4PM，BIW方法下，从19号至6号被试的Bias与2PM，3PM下的情况相似，Bias的绝对值逐渐增大。从6至1号被试的Bias的绝对值逐渐减小。这也就是说，原来在2PM，3PM模型下的能力低估现象，在4PM，BIW方法得到有效的纠正。而且，在4PM，BIW方法下的Bias值在5至7号被试之间发生了拐点，也就是说，当被试所错前两题的难度小于被试能力估计值约0.9至1.5之间，4PM，BIW方法对被试能力估计值逐渐产生了纠正作用。

总之，由表1中2PM的结果可知，CAT考试现象是被试作答异常现象(猜测、睡眠现象)、数学模型(2PM)两方面因素共同影响的结果。以往CAT实践中主要使用1PM、2PM，因而容易出现被试能力高估和低估现象。

4对四参数模型持不同观点的讨论

Green(2011)对CAT初始阶段前两题作答失误现象进行模拟研究，得到与Rulison和 Loken(2009)类似的结果，即前两题作答失误会导致被试能力低估现象。Green(2011)采用忽略失误作答，和将失误作答为改正确作答两种方式进行纠正，发现部分被试能力被高估了0.10左右。本文认为，这是由于Green的纠正方法过于简单导致的。由本文结果可知，四参数模型和2PM-BIW不会导致纠正幅度过大的情况。

Green(2011)没有对四参数模型进行模拟，但Green却不赞成四参数模型的使用，认为(1)Rulison 和 Loken的研究是单纯的选择了高能力被试作为典型代表；(2)Bias相对较大是IRT在能力量尺两端的拉伸造成的；(3)高能力被试很少答错中等难度试题；(4)4PM在运用中可能存在参数较难估计，测验信息量会相对减少从而误差增大。本文认为，Green以上四个论据是片面的。本文提出以下探讨：(1)本文从低能力到高能力被试都选择了代表性的样本，由模拟结果发现，被试答错或答对前两题所造成的能力高估现象或低估现象是一种趋势，而不是典型的个案现象；也不是IRT能力量尺两端造成的，而是一个规律性的变化。(2)以四参数模型为例，假设γ=0.95，c=0.20，某一高能力被试(以θ=2.1为例)同时答错前两道中等难度试题(b=0.0)的概率为0.44%，那么高能力被试就可能被低估，低估幅度为-0.306，如果换算为500+100*θ，将是30分的幅度。只要高能力被试群体中有存在着能力低估的一定程度概率，就说明2PM在CAT测试中存在缺陷，需要进行改进。(3)WINSTEPS软件(Linacre，2012)包含了四参数模型参数估计。Loken & Rulison(2010)使用贝叶斯方法实现了对四参数模型的参数估计，即项目参数估计的难题已经解决了；(4)在实际测量中，假设一个测验已经对被试进行了测试，那么测量误差就是固定的。使用单参数模型，还是四参数模型来计算测量项目信息量和测量误差，都不会改变这个测验的实际测量误差。Magis(2013)探讨了在四参数模型下一道试题的最大项目信息量所对应的最佳能力估计值，并论述了4PM下最大项目信息量的应用。

也许有研究者疑虑，在测验中被试作答的“猜测”和“睡眠”现象都是属于少数情况，是否需要使用较复杂的四参数模型来估计不同类型的被试?本文对此的观点是：(1)从数学公式可知，两、三参数模型都是四参数模型的特例，两、三参数模型可以适合的测验，四参数模型也可以适合。(2)如果测验中被试作答的“猜测”和“睡眠”现象都是属于少数情况，那么使用四参数模型估计出的c，γ参数也将相对较小。根据论文简小珠，张敏强和彭春妹(2010)中的图1，图2及其数据，如果某一试题的c，γ参数很小(例如c=0.001，或γ=0.999)，那么该试题对被试能力估计影响接近于两参数模型(c=0，γ=1)。如果该被试答对试题的难度在区间-

5结论

在2PM下CAT初始阶段前两题的作答时，只有被试作答情境为睡眠现象时会导致能力相对低估现象，猜测现象时会导致高估现象，这较好的说明了“CAT初始阶段作答影响最终成绩”考试现象发生的具体情境。CAT考试现象是被试作答异常现象(猜测、睡眠现象)、CAT数学模型(2PM)共同影响的结果。3PM、4PM、2PM-BIW可以有效纠正能力高估现象，纠正作用产生的拐点在当被试所答对试题的难度大于被试能力估计值时且区间大约为0.9

参考文献

简小珠，戴海崎，彭春妹.(2007).IRT中Logistic模型的c、γ参数对能力估计的改善.心理学报，39(4)，737-746.

简小珠，张敏强，彭春妹.(2010).四参数Logistic模型研究进展及其评析.心理学探新，30(3)，69-73.

张华华.(2002).计算机自适应考试设计中的误区.考试研究，第二辑，35-39.

张华华，程莹.(2005).计算机化自适应测验(CAT)的发展和前景展望(续).考试研究，1(2)，22-41.

Bock，R.J.，& Mislevy，R.D.(1982).Adaptive EAP estimation of ability in a microcomputer environment.AppliedPsychologicalMeasurement，6，431-444.

Chang，H.H.，& Ying，Z.(2008).To weight or not to weight?Balancing influence of initial items in adaptive testing.Psychometrika，73(3)，441-450.

Green，B.F.(2011).A Comment on Early Student Blunders on Computer-Based Adaptive Tests.AppliedPsychologicalMeasurement，35(2)，165-174.

Linacre，J.M.(2012).Winsteps®Raschmeasurementcomputerprogram.Beaverton，Oregon：Winsteps.com.

Loken，E.，& Rulison，K.L.(2010).Estimation of a four-parameter item response theory model.BritishJournalofMathematicalandStatisticalPsychology，63，509-525.

Magis，D.(2013).A Note on the Item Information Function of the Four-Parameter Logistic Model.AppliedPsychologicalMeasurement，35(2)，304-315.

Merritt，J.(2003).WhythefolksatETSflunkedthecourse—atech-savvyservicewillsoonbegivingB-schoolapplicantstheirGMATs.Business Week.

Mislevy，R.，& Bock，R.(1982).Biweight Estimates of Latent Ability.EducationalandPsychologicalMeasurement，42，725-737.

Rulison，K.L.，& Loken，E.(2009).I’ve Fallen and I Can’t Get Up：Can High-Ability Students Recover From Early Mistakes in CAT?AppliedPsychologicalMeasurement，33(2)，83-101.

Wright，B.D.(1977).Solving measurement problems with the Rasch model.JournalofEducationalMeasurement，14，97-116.

Yen，Y.，Ho，R.，Laio，W.，Chen，L.，& Kuo，C.(2012).An empirical evaluation of the slip correction in the four parameter logistic models with computerized adaptive testing.AppliedPsychologicalMeasurement，36(2)，75-87.

The First Several Responses in CAT Determine the Final Score? The Cause and Corresponding Countermeasure to the CAT Phenomenon

Jian Xiaozhu1，2，Dai Haiqi2

(1.School of Educational Science，Shangrao Normal University，Shangrao 334001；2.School of Psychology，Jiangxi Key Laboratory of Psychology and Cognitive Science，Jiangxi Normal University，Nanchang 330022)

Abstract：Some researchers had analyzed the CAT event and believed that：if the examinees make correct answers on the first several items，he may gain relatively high score even if he does not well in the next many items；if the examinees make wrong answers on the first several items，his ability may be underestimated even if he do well in the next many items.The author names these phenomena as the CAT phenomena，that is，the first several responses in cat determine the final score.Many researchers have proposed some methods to rectify overestimation and underestimation.To determine the extent of bias at various ability levels，a set of CAT simulations were carried out.According the results，low-ability examinees get the first two items and their Biases are become bigger significantly，which is named as ability overestimation phenomenon.High-ability examinees miss the first two items and their Biases are become smaller significantly，which is named as ability underestimation phenomenon.Under 3PM，4PM，BIW，the Biases of low-ability examinees become smaller than that of 2PM in second case when they get the first two items by chance，and the ability overestimation phenomenon is rectified well.Under 4PM，or BIW，the absolute of the Biases of high-ability examinees become smaller than that of 2PM in third case when they miss the first two items，and the ability underestimation phenomenon is rectified well also.Therefore，in the three simulated CAT cases，4PM，BIW rectify the underestimation phenomenon and overestimation phenomenon.

Key words：CAT；CAT simulation；guessing phenomenon；sleeping phenomenon；overestimation；underestimation

*基金项目：江西省高校人文社会科学项目(XL1515)，江西省社会科学规划青年项目(13JY47)，广州市基础教育学业质量监测系统建设项目(GZIT2013-ZB0465)，国家自然科学基金项目(31260238)。

通讯作者：戴海琦，E-mail：daihaiqi@aliyun.com。

中图分类号：B841.2

文献标识码：A

文章编号：1003-5184(2016)03-0276-05