《条件推理的条件概率模型》的新进展*

胡竹菁　胡笑羽

(江西师范大学心理学院，江西省心理与认知科学重点实验室，南昌 330022)



《条件推理的条件概率模型》的新进展*

胡竹菁胡笑羽

(江西师范大学心理学院，江西省心理与认知科学重点实验室，南昌 330022)

摘要：推理心理学中的任何重要的理论模型在提出后都有一个不断修订和完善的发展过程。Oaksford等为了解释他们在“Wason四卡片选择任务”的实验研究结果，于1994年提出了“最佳数据选择模型”；2000年将这一模型扩展为“条件推理的条件概率模型”用于解释人类进行条件推理的心理加工机制；2007年又将这一模型做了新的修订。本文拟对这一模型新进展的内涵介绍给我国对推理心理学研究领域有兴趣的研究者。

关键词：条件推理；最佳数据选择模型；条件推理的条件概率模型

1引言：心理学研究“条件推理”的三种实验范式

心理学研究中的“条件推理”通常是指形式逻辑学中所说的“充分条件假言推理”。在形式逻辑学中，“‘充分条件假言命题’是反映某事物情况是另一事物情况充分条件的假言命题，其一般形式为：‘如果p，那么q’……‘充分条件假言推理’是指“一个前提为充分条件假言命题，另一个前提和结论为性质命题的假言推理”。

形式逻辑学指出，“充分条件假言推理”具有表1所示的四种推理形式，其中只有“肯定前件式”和“否定后件式”是可以推出有效结论的推理形式，其他两种形式的推理是不能推出有效结论的(《普通逻辑》编写组，2011)。

表1　包含充分条件假言命题“如果P，那么Q”的四种条件推理形式

推理心理学是一门用心理学的实验研究方法来研究人类进行推理这一心理加工过程中有关规律的心理学分支学科。心理学对“条件推理”的研究主要包括三种实验范式：(1)演绎推理实验范式；(2)Wason四卡问题实验范式；(3)概率推理实验范式。

所谓“条件推理的演绎推理实验范式”，是指由“如果p，那么q”这一条件命题建构的四种推理形式在形式逻辑学中一般属于“演绎推理”的研究范畴。早期推理心理学家对这种推理的心理加工过程进行实验研究时，所采用的实验范式主要是以表1中的四种不同推理形式的推理题作为实验材料，要求没有受过形式逻辑专门训练的成人(主要是大学生)对每一种推理题判定“推理结论是否可以从两个前提中推论出来”，然后根据对他们的推论结果进行统计分析后来寻找人类在完成条件推理过程中的有关心理加工规律。早期主要研究结果有如表2所示。

表2　三种不同研究中成人被试认可条件推理的百分率统计表(引自Evans，1982)

由表2所列资料可知，这些实验结果具有大体一致的作答模式。其中：肯定前件式是常被认可的；认可否定后件式的人次居于第二位。否定前件式和肯定后件式两种条件下的反应次数则总是差不多。

所谓“Wason四卡问题实验范式”，是指由Wason于1966年开创性设计的实验范式，目的在于探求“被试对给定条件法则的真伪进行验证时的心理活动规律”。由于这种范式的实验过程通常是让被试对给定的与表1中四种推理形式的结论相对应的四张卡片进行选择来进行，因此，后来有关这一领域的研究通常被称为“Wason四卡片问题(或Wason选择作业)”。在Wason的“四卡片选择作业”的实验范式中，给被试看图1所示的四张卡片：

图1　“Wason四卡片选择作业”实验范式示例图

然后，主试要求被试思考为了证实 “如果卡片的一面是元音字母，那么它的另一面就是偶数” 这一条件命题(在这种实验范式中，通常把“如果p，那么q”这种条件命题称为“法则(rule)”，本研究中这两个概念相通)的真伪，必须翻看哪些卡片。图1的四张卡片中，与“前件事件P(即元音字母)”对应的是标记为“E”的卡片，相应地，“前件事件的否定‘-P’”为“F”卡片，“后件事件Q(即偶数数字)”为“4”卡片，“后件事件的否定‘-Q’”为“7”卡片。由此可知，从某种意义上说，“Wason四卡问题实验范式”是对“演绎推理实验范式”的变通研究。这种研究范式最为典型的研究结果之一有如表3所示。

表3　被试在Wason四卡问题上所作选择的百分比

研究者根据诸如表3所示的实验结果认为被试在实验条件下表现出了强烈的证真倾向。

按照逻辑学的传统观点，凡是从个别知识的前提推出一般知识的结论的推理，称之为归纳推理。主要包括“完全归纳推理”、“不完全归纳推理”和“典型归纳推理”等类别。在“不完全归纳推理”中又包括“概率归纳推理(以称统计归纳推理)”，这是指“根据被考察的样本中百分之几的对象具有(或不具有)某种属性，从而推出总体百分之几的对象具有(或不具有)某种属性”的推理。

心理学研究中的“条件推理的概率推理实验范式”，主要是指“以表1中的四种不同推理形式为实验材料，让没有受过形式逻辑专门训练的成人(主要是大学生)对其进行概率解题后，通过分析他们的概率推理结论与推理题中条件命题的‘条件概率’、‘前件概率’和‘后件概率’的相互关系进行统计分析来寻找人类对条件推理进行概率解时的有关心理加工规律”的实验范式。条件概率推理是最近二十年来西方推理心理学的研究热点之一，有许多心理学家对此进行过研究，并且在实验研究的基础上，有许多推理心理学家试图根据实验结果对“推理者为什么会在不同推理形式的推理过程中犯错误”等问题提出自己的理论解释，其中，Oaksford等提出的“条件推理的条件概率模型”是其中影响较大的理论模型之一(Oaksford et al.，2000，2007，2010)。

就像推理心理学中其他的理论模型那样，Oaksford等在对“条件推理”进行实验研究的基础上所提出的 “条件推理的条件概率模型”也有一个从提出到完善的发展过程。本文拟对这一模型新进展的内涵介绍给我国对推理心理学研究领域有兴趣的研究者。

2从“最佳数据选择模型”到“条件推理的条件概率模型”

1994年，Oaksford和Chater在对上述有关条件推理第二种研究范式即“Wason四卡片选择任务”进行实验研究的基础上，在美国心理学会主办的著名学术期刊《心理学评论》(Psychological Review)上发表了题为“作为最佳数据选择的选择任务的理性分析”一文，文中首次表述了一个通过概率方法(probability approach)来解释Wason四卡片选择任务的理论模型，他们把这一模型称之为“最佳数据选择模型(optimal data selection model，ODSM模型)”，2003年，他们对“最佳数据选择模型”进行了更新和发展。余达祥等(2008)对Oaksford等的“最佳数据选择模型”做了较为全面的介绍。

Eysenck等人指出“这个理论是根据概率论来分析所给推理问题的前提条件的。通过分析前提条件，我们可以预测从问题的所有可能结论中能够获取的信息的多少，同时根据能够获取信息的多少，我们也可以预测人们最有可能作出什么反应。也即人们最有可能推导出含信息量最大的结论，其次是含信息量稍次的结论。”总之，Eysenck等人认为“最佳数据选择模型”的核心思想是：“本质上人们并不是进行推理而是最大程度地获取信息。也就是说，人们在作决定时旨在减少情境的不确定性以及获得更多现实世界的信息。所以，在选择任务中，人们总是作出最有价值的选择，他们总是选择那些概率最大的卡片”(Eysenck & Keane，2000)。

余达祥等(2008)认为：“Oaksford等的最佳数据选择模型为华生四卡问题实验结果提供了一种全新的解释。该模型的提出及其与相关实验数据的一致性，表明人们面临推理问题时可以启动多种处理机制。解决逻辑问题并非一定需要启动逻辑推理机制，即存在非逻辑的推理机制。Oaksford等的最佳数据选择模型所表述的，就是这类非逻辑的条件推理机制。”

推理心理学家通常认为人们进行“条件推理”的心理加工机制与“Wason四卡问题”的解决机制是相通的，因此，在“最佳数据选择模型”基础上，Oaksford等于2000年将“最佳数据选择模型”的内涵进行修改后用于解释人类进行“条件推理”的心理加工机制，他们将修改后的理论称之为“条件推理的条件概率模型(a conditional probability model of conditional reasoning)”。胡竹菁(2008)将这一模型的基本观点概括为四个方面对Oaksford等2000年版的这一模型进行过较为详尽的评述。

Oaksford等在2007年之后对这一模型进行了较大的修订(Oaksford et al.，2007，2010)。由于“条件推理的条件概率模型”在发展过程中，同一符号经常在不同时期的模型中被用于表达不同的含义，反之，同一事件的概率值经常使用不同的符号来表示，因此，在对这一理论模型的新进展进行介绍之前，我们有必要对该模型发展过程中不同时期所涉及到的几种概率事件及对应的符号加以厘清：

在1994年首次论述他们的“最佳数据选择模型”时，对于像“如果A，那么B”这样的条件命题，他们小写字母“a”来表示条件命题中“前件事件A”的概率值，即“a=P(A)”，用小写字母“b”来表示该条件命题在“前件事件A”不出现但非A出现的条件下，“后件事件B”出现的条件概率值，即“b=P(B/-A)”；由此建构的这一条件命题中“前件A”和“后件B”之间相互依赖型的概率关系列联表为：

表4　条件命题“如果A，那么B”前后件

注：a=P(A)，b=P(B /-A)

2000年，Oaksford等人在首次论述“条件推理的条件概率模型”时，对表4所示条件命题“如果A，那么B”前后件相互依赖模型概率关系列联表进行了重构，在重构后的列联表中仍然用小写字母“a”来表示条件命题中“‘前件事件A’的概率值，即a=P(A)”，但是，小写字母“b”则改为用来表示条件命题中“‘后件事件B’的概率值，即b=P(B)”此外，用“例外参数ε(exceptions parameter)”来表示“在‘前件事件A’出现的条件下，‘后件事件B’不出现(即‘非B’或‘-b’)的条件概率值，即ε=P(-B/A)”，由此建构的这一条件命题中“‘前件事件A’和‘后件事件B’之间相互依赖型的概率关系列联表就有如表5所示。

表5　条件命题“如果A，那么B”前后件

注：a=P(A)；b=P(B)；ε为例外参数，ε=P(-B/A)

2007年，Oaksford和Chater在修正版的“条件推理的条件概率模型”中，一方面，将模型中涉及的几种概率都相应地区分为“先验概率”和“后验概率”，另一方面，不再使用“例外参数ε”，而是直接使用“条件命题的‘条件概率值’”。具体而言，他们用小写字母“a”来表示“如果A，那么B”这一条件命题中“在‘前件事件A’出现的条件下，‘后件事件B’出现的先验条件概率值，即a=P0(B/A)”，用小写字母“c”来表示条件命题中“前件事件A的先验概率值，即c=P0(A)”，用“1-b”来表示条件命题中“后件事件B的先验概率值，即P0(B)=1-b”。这样，重构的这一条件命题中“前件事件A”和“后件事件B”之间相互依赖型的概率关系列联表就成为：

表6　条件命题“如果A，那么B”前后件

注：a=P0(B/A)；c=P0(A)；P0(B)=1-b

Oaksford和Chater在2010年的文章中再次论述“条件推理的条件概率模型”的有关议程表达式时，仍然用小写字母“a”来表示“如果A，那么B”这一条件命题中“在‘前件事件A’出现的条件下，‘后件事件B’出现的先验条件概率值，即a=P0(B/A)”，但是，他们改用小写字母“b”来表示条件命题中“‘前件事件A’的先验概率值，即b=P0(A)”，改用小写字母“c”来表示条件命题中“‘后件事件B’的先验概率值，即c=P0(B)”。

如上所述，鉴于Oaksford和Chater不同时期论述他们的模型时使用了不同的符号表达同一事件的含义，这容易引起读者在理解他们模型内涵时产生不必要的混淆，因此，在正确理解Oaksford和Chater于2007年专著中所论述的“条件推理的条件概率模型”修订版内涵的基础上，我们觉得在介绍这一模型新进展的内容之前，有必要对上述有关“如果A，那么B”这一条件命题中有关“前件事件A的概率”“后件事件B的概率”和“该命题的条件概率”的表达符号做以下两方面的约定：

(1)用符号“P0”表示这三种事件的“后验概率”，用符号“P1”表示这三种事件的“后验概率”；

(2)小写字母“a”来表示“如果A，那么B”这一条件命题中“前件事件A的先验概率，即a=P0(A)”，小写字母“c”表示该条件命题中“后件事件B的先验概率，即b=P0(B)”，小写字母“c”表示该条件命题中“‘前件事件A’发生的条件下，‘后件事件B’发生的条件概率值，即c=P0(B/A)”。

在上述有关符号约定的基础上，下面我们来介绍Oaksford和Chater在2007年出版专著中所论述的“条件推理的条件概率模型”的新内涵。

3“条件推理的条件概率模型”的新内涵

2007年修订版的“条件推理的条件概率模型”与2000年最初提出模型相比较，其内涵总体上说仍然可以概括为相同的四个方面，但由于新模型对相应事件的概率值做了“先验概率”和“后验概率”的区分，由此决定了这四方面内容与2000年版的相应内涵存在不一样的表达方式。修订版的“条件推理的条件概率模型”的四方面内容分别是：

(一)与条件命题“如果A，那么B”建构的四种推理形式有关三种事件的概率值都可以区分为“先验概率P0”和“后验概率P1”两大类

推理者对诸如“如果A，那么B”这样的条件命题构成的推理题进行条件推理的心理加工过程中存在以下三类相关事件的概率，其中每一类概率都包括“先验概率P0”和“后验概率P1”两大类：

1．“前件事件A”发生的可能性，用符号“P0(A)”表示其“先验概率”，“P1(A)”表示其“后验概率”；

2．“后件事件B”发生的可能性，用符号“P0(B)”表示其“先验概率”，“P1(B)”表示其“后验概率”；

3．“在条件命题中的‘前件(或后件)事件’出现(或不出现)的条件下，该条件命题的‘后件(或前件)事件’出现(或不出现)的条件概率”，这包括与表1所示四种情况相应的四种不同形式的条件概率，即“P(B/A)”，“P(-B/-A)”，“P(A/B)”和“P(-A/-B)”，每种条件概率都可以区分为“先验概率P0”和“后验概率P1”两大类。

(二)使用一个2X2列联表来表示条件命题“如果A，那么B”中“前件事件A”和“后件事件B”之间相互依赖型的先验概率关系

若使用前面约定的符号来表达与“如果A，那么B”这一条件命题相关联的几种事件的概率值，那么，该条件命题中“前件事件A”和“后件事件B”之间相互依赖型的先验概率关系列联表就有如表7所示。

表7　条件命题“如果A，那么B”前后件

注：a=P0(A)；b=P0(B)；c=P0(B/A)

(三)建构相应的方程式来计算相应推理结论的后验概率

对于‘如果A，那么B’这一条件命题所构成的四种不同形式的条件推理，可以利用表8中所示的各种前后件先验概率之间的关系，建构相应的方程式来计算相应推理结论的后验概率。

当“前件事件A的后验概率P1(A)=1”时，推理者对于表1所示的MP，DA，AC和MT等不同条件推理形式，计算相应推理结果后验概率的方程式分别有如表8所示。

表8　计算各种条件推理概率值的方程表达式表

(四)利用“先验结论概率”和“后验结论概率”的概念对2000年版模型中有关四种推理预测结果的图示内涵做了重新论述

Oaksford等2000年版“条件推理的条件概率模型”对人们进行条件推理的最重要的预测是“推理者对上述四种不同形式的条件推理的认可程度主要是与范畴前提的概率(在给定范畴前提的条件下得出相应结论的概率)成正比的(proportion)。”

修订后的“条件推理的条件概率模型”对第四方面的内容改为“推理者对DA、AC和MT等三种不同形式条件推理的‘后验结论概率P1(结论)’将作为一个函数，随着相应推理形式的‘范畴前提的先验P0(前提)’和‘推理结论的先验概率P0(结论)’的取值变化而变化”。

以“‘如果A，那么B’这一条件命题有关‘前件事件A’出现的条件下‘后件事件B’出现的‘先验条件概率P0(B/A)=0.75’”为例，这时有关“DA”、“AC”和“MT”等三种形式条件推理结论的后验概率值就改为如图2所示。

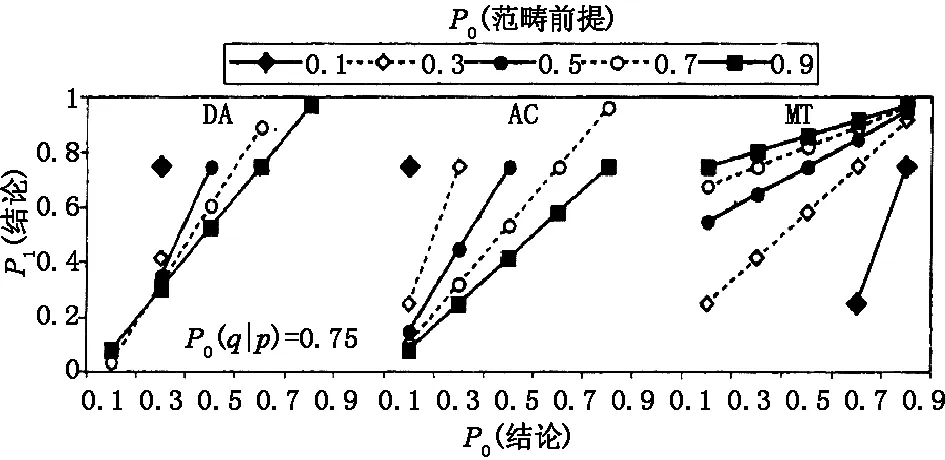
图2　DA，AC和MT三种条件推理后验结论概率与其范畴前提和结论的先验概率相互关系图

胡竹菁(2008)曾经对Oaksford等在2000年论文中有关这些图示的内涵进行过解读。将图2与该模型2000年版的图示进行比较可以知道，图2中最重要的修改是“用X-轴表示相应条件推理的先验结论概率的不同取值，用纵轴表示通过表8中所示相应条件推理计算方程计算出的不同后验结论概率值”。下面，我们以图2中左边的“DA”图示为例，来看看如何理解该图所示内涵。条件命题“如果A，那么B”完整的“否定前件式(DA)”的推理形式是：

如果A，那么B

非A

所以，非B

“给定范畴前提”则是指横线上面的第二前提“非A”(用符号“-A”表示，意指前件A不出现)；“推理结论”是指横线下的“非B”(用符号“-B”表示，意指后件B不出现)。

根据Oaksford等修订版的“条件推理的条件概率模型”，在“前件事件A发生的条件下后件事件B发生的先验条件概率P0(B/A)=0.75”，以及“范畴前提的先验概率P0(-A)”取值不同的情况下，其“结论的后验概率”有如图2中左边的“DA”图示。图中，X-轴表示这一推理结论的“结论的先验概率P0(-B)”的不同取值。条件推理中“范畴前提的后验概率值”通常总是假定为“1”，例如，在否定前件式DA的推理中，总是假定其“范畴前提的后验概率P1(-A)=1”。图中不同类型的曲线表示“观察到的结论后验概率P0(-B/-A)=P1(-B)”，作为“结论先验概率P0(-B)”的函数是怎样随着“范畴前提的先验概率P0(-A)=1-P0(-A)”的不同取值而变化的。“结论的先验概率”和“范畴前提的先验概率”两者的取值范围都在0.1-0.9之间，变化的间距为0.2。由图示可知。

由“条件推理的条件概率模型”可知，对推理规则“如果A，那么B”进行“否定前件式DA”的推理时，计算其“推理结论的后验概率P1(-B)”的数学表达式是：

“范畴前提”是指推理式中的第二前提即“非A”，其“先验概率P0(-A)”的取值范围是“0.1，0.3，0.5，0.7，0.9”，P0(-A)的取值不同，图示中的曲线类别就不同(如“空心圆曲线表示P0(-A)=0.7时计算得出的P1(-B)概率值”；“黑色正方形曲线表示P0(-A)=0.9时计算得出的P1(-B)概率值”)。

下面我们以“范畴前提先验概率P0(-A)=0.9”为例，看看“否定前件式DA推理结论的后验概率P1(-B)”是怎样随着其“推理结论的先验概率P0(-B)”的取值变化而变化的。

如图2所示，已知

“c=P0(B/A)=0.75”，

当“P0(-A)=0.9”时，“a=P0(A)=1-P0(-A)=1-0.9=0.1”，“推理结论的先验概率P0(-B)(即‘-b’)” 的取值范围是“0.1，0.3，0.5，0.7，0.9”，因为“b=P0(B)=1-P0(-B)”，因此，对应的“b值”则分别为“0.9，0.7，0.5，0.3，0.1”，将

可得：

当P0(-B)=0.1时，b=0.9：

当P0(-B)=0.3时，b=0.7：

当P0(-B)=0.5时，b=0.5：

当P0(-B)=0.7时，b=0.3：

当P0(-B)=0.9时，b=0.1：

上述各式的计算结果表明，在“范畴前提先验概率P0(-A)” 的值不变并且“前件A出现的条件下后件B出现的‘先验条件概率P0(B/A)=0.75’” 的情况下，否定前件式条件推理的“推理结论的后验概率P1(结论)”是随着该推理形式的“推理结论的先验概率P0(结论)”取值的变化而变化的：P0(结论)高则P1(结论)也高，P0(结论)低则P1(结论)也低。

因此，推理者对DA条件推理“推理结论的后验概率P1(结论)”，在给定“范畴前提‘非A’的先验概率P0(-A)”为某个固定值的条件下，与该推理形式“推理结论的先验概率P0(结论)”成正比。

4结语

作为心理学最近几十年的研究热点之一，推理心理学有着越来越多的研究成果公布于世。我们在把握这一研究领域的经典实验研究范式和重要理论模型时，应该注意各种模型在提出后不断修订和完善的发展过程。就如本文所介绍的Oaksford等的“条件推理的条件概率模型”，最早提出时是用于解释“Wason四卡片选择任务”的“最佳数据选择模型”；而后扩展为用于解释人类进行条件推理的心理加工机制的“条件推理的条件概率模型”；2007年后又以区分“先验概率”和“后验概率”为主要特征将这一模型做了新的修订。不断把握各种重要的推理心理学理论模型的新进展内容，才能使我国推理心理学的研究有更好的基础。

参考文献

《普通逻辑》编写组.(2011).普通逻辑(第5版).上海人民出版社.

胡竹菁.(2008).条件推理的条件概率模型述评.心理学探新，28(2)，25-32.

余达祥，胡竹菁，王平.(2008).最佳数据选择模式.心理学探新，28(2)，33-35.

Evans，J.St.B.T.(1982).Thepsychologyofdeductivereasoning.London：Routledge & Kegan Paul.

Eyssenck，M.W.，& Keane，M.T.(2000).Cognitivepsychology.Psychology Press，Ltd.

Johnson-Laird，R.N.，& Wason，P.C.(1970).Insight into a logical relation.QuarterlyJournalofExperimentalPsychology，22，49-61.

Oaksford，M.，& Chater，N.(1994).A Rational Analysis of the Selection Task as Optimal Data Selection.PsychologicalReview，101(4)，608-631.

Oaksford，M.，& Wakefield，M.(2003).Data selection and natural sampling：Probabilities do matter.MemoryandCognition，31，143-154.

Oaksford，M.，& Chater，N.(2007).Bayesianrationality：Theprobabilisticapproachtohumanreasoning.Oxford：Oxford University Press.

Oaksford，M.，& Chater，N.(2010).Cognitionandconditionals.Oxford：Oxford University Press.

Oaksford，M.，Chater，N.，& Larkin，J.(2000).Probability and polarity biases in conditional inference.JournalofExperimentalPsychology：LMC，4，883-899.

Conditional Reasoning：The Comparison between the Two Experimental Research Approaches of “Deduction” and “Probability”

Hu ZhujingHu Xiaoyu

(School of Psychology，Jiangxi Normal University，Key Laboratory of Psychology and Cognition Science of Jiangxi，Nanchang 330022)

Abstract：Any important theory in human reasoning research field as its own development process.Oaksford and his colleagues propose “The optimal data selection model” based on their experiment research for “The four cards selection task” in 1994.In 2000，the model has been revised into “The conditional probability model of conditional reasoning” to explain human’s conditional reasoning by the authors，and a new revision of the model has been made again in 2007.This paper will give a detail introduction to the new revision of the model.

Key words：conditional reasoning；optimal data selection model；the conditional probability model of conditional reasoning

*基金项目：国家自然科学基金项目(31460252)，江西省社会科学2013年规划课题(13jy22)。

通讯作者：胡竹菁，E-mail：huzjing@jxnu.edu.cn。

中图分类号：B842.5

文献标识码：A

文章编号：1003-5184(2016)03-0211-06