基于马尔科夫链-复杂网络事故传播的罐区储罐失效概率研究
2016-07-13许飞云张炎冰东南大学机械工程学院南京89江苏省特种设备安全监督检验研究院南通分院南通6000
宗 辉 许飞云 张炎冰(.东南大学机械工程学院 南京 89)(.江苏省特种设备安全监督检验研究院南通分院 南通 6000)
基于马尔科夫链-复杂网络事故传播的罐区储罐失效概率研究
宗辉1许飞云1张炎冰2
(1.东南大学机械工程学院 南京 211189)
(2.江苏省特种设备安全监督检验研究院南通分院 南通 226000)
摘 要:通过对国内外储罐失效概率研究方法的分析,本文引入复杂网络事故传播理论和马尔科夫链,建立基于马尔科夫链的复杂网络事故传播模型,以解决传统方法涉及较少的储罐之间的n-n相互作用问题。并进行实例分析,将该模型计算结果与传统方法进行对比,结果表明,该模型计算结果能为安全防范提供了更好的建议。
关键词:储罐失效概率 复杂网络事故传播 马尔科夫链
罐区化学品数量大、种类多,大多易燃易爆、有毒有害,一旦储罐产生严重缺陷,发生泄漏,容易引发火灾、爆炸、中毒等灾难性事故,极易给人民生命财产安全等造成严重危害或威胁。经国家安全监管总局事故查询系统,统计出2005~2014年全国范围内造成重大人员伤亡的罐区泄漏、火灾、爆炸事故案例共计21起。因此,在当前储罐安全问题突出的背景下,对罐区储罐失效概率问题的研究显得尤为必要。
国外对储罐失效概率的研究起步较早。意大利学者Valerio Cozzani和Ernesto Salzano着重对爆炸冲击波多米诺效应进行了研究,并给出了基于多米诺效应的储罐失效概率的计算模型[1-3]。美国石油协会API采用基于统计数据的通用失效概率乘以设备的损伤因子的方法来确定具体设备的失效概率。在国内,东北大学从2003年始,基于多米诺效应开展对化工园区危险性、园区重大危险源分级、重大事故多米诺效应等的研究[4-6]。大连交通大学王洪德等人基于网格划分和风险叠加原理计算化工园区安全风险的失效概率和失效后果[7]。
然而,API的失效概率计算方法多采用分级赋值方法,各个修正因子的赋值相乘后导致累积误差,评价精度有待提高。基于叠加原理[8]的计算方法,只是将多个邻近对象对当前目标的影响结果简单叠加,影响权重相等,忽视了研究对象的个体性差异。而基于多米诺效应的失效概率计算方法[9,10]对于解决事故储罐对其他储罐的作用问题效果明显,即解决1-n问题,但是随着相互作用的储罐数目激增,误差随着增大。因此,就目前对储罐失效概率研究而言,研究较少且远未达到有效解决储罐安全问题的程度。本文将在前人的多米诺效应理论研究的基础上,引入复杂网络传播理论[11-12]和马尔科夫链[13],尝试建立罐区储罐失效概率模型,进一步探讨罐区内各个储罐之间的相互作用,即可以初步解决 n−n问题。
1 复杂网络事故传播理论
复杂网络是大量相互作用的节点集合,是节点作用效果通过拓扑结构进行传播的网络。基本参数包括度及度分布等。复杂网络中某节点的度表示该节点与网络中其他节点相连的边数。边数越多,说明该节点在网络中的重要性越大。
如图1所示,罐区中各个储罐为复杂网络中的节点,各个储罐风险通过拓扑结构相互作用,从而构成了罐区的复杂事故传播网络。将图1的罐区储罐分布关系抽象为图2所示的网络拓扑示意图(只有箭头相连的两个储罐之间才会发生相互作用)。该网络共有n个节点,各个节点有两种状态:S和I。S指与事故节点相连但没有发生事故的储罐节点,称为易感染节点;I指已经发生事故的储罐节点,称为事故节点。借鉴经典传染病SI模型[11],建立事故扩散模型。如式(1):
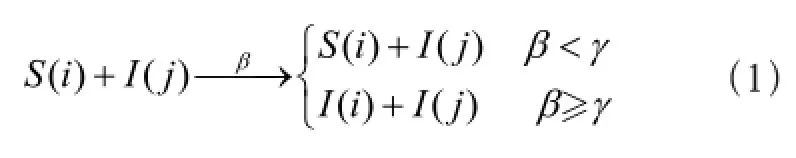
式中:
β——储罐节点i事故感染概率;
γ——储罐节点i的事故免疫概率,其值等于风险可接受水平10-4。
储罐的事故感染率β可以由式(2)求得:

式中:
pi——储罐i本身的失效概率;
pji——在储罐j失效后对储罐i的作用概率;
ki——权重系数。

图1 罐区整体分布图
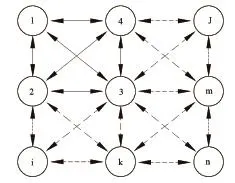
图2 罐区网络拓扑示意图
2 罐区储罐失效概率模型
2.1 状态转移矩阵
对于罐区节点网络而言,储罐节点当前时刻t的失效概率只与t-1时刻的状态有关,与t-1时刻之前的状态无关。又由于时间取值连续,故其属于时间连续的马尔科夫链。
设节点j对节点i的作用为pji,则该复杂网络事故传播的状态转移矩阵可以表示为:
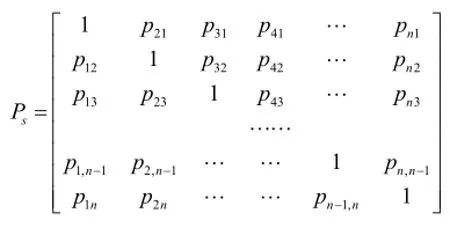
式中:
pji——在储罐j失效后对储罐i的作用概率。
值得注意的是,罐区内地理位置相连的储罐节点受直接影响最大,当地理距离增大时直接影响急剧减小至可以忽略,故
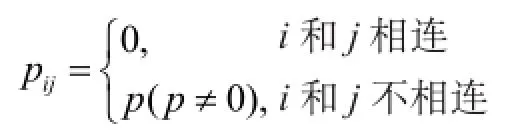
2.2 基于马尔科夫链的复杂网络事故传播模型
假设初始事故源只有一个,则选中储罐i的可能性为ki,ki的大小与储罐本身失效概率以及罐区内整体失效水平有关。ki可由式(3)计算得:

对于储罐i而言,t时刻的失效概率只与罐区内各储罐t-1时刻的状态有关,则t时刻储罐i的失效概率为:
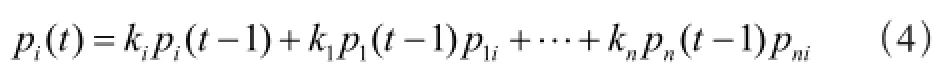

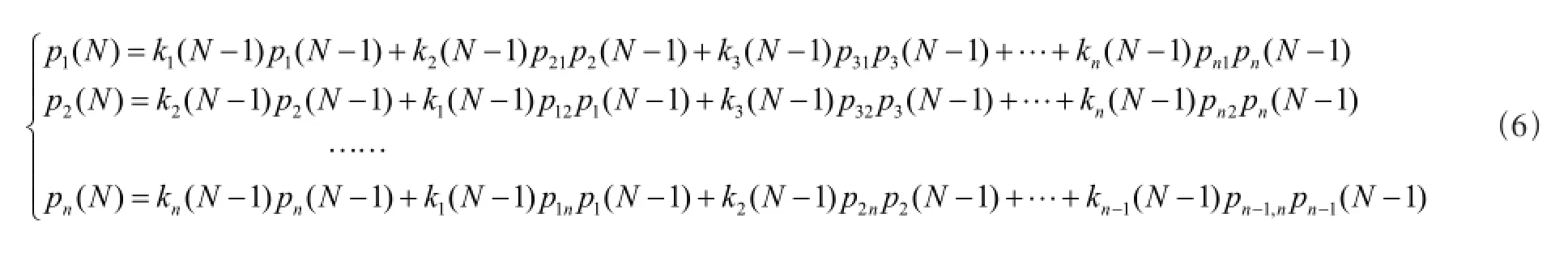
对于上述方程组迭代有两种结果:(a)收敛;(b)不收敛。下面分别对这两种情况展开说明:
1)迭代收敛 若方程的解迭代收敛P( n)→P,则称该随机过程趋于定常态分布。此时,无外部作用力介入时,罐区网络事故率趋于平衡态。
2)迭代不收敛 对于迭代不收敛问题,当节点i的事故感染概率大于免疫概率10-4时,认为此节点处储罐已经被感染,由易感染态S(i)转化为已感染态I(i)。此时,邻近储罐j对这一节点失去事故传染作用,即Pji=0。以节点3为例,修正状态转移矩阵为
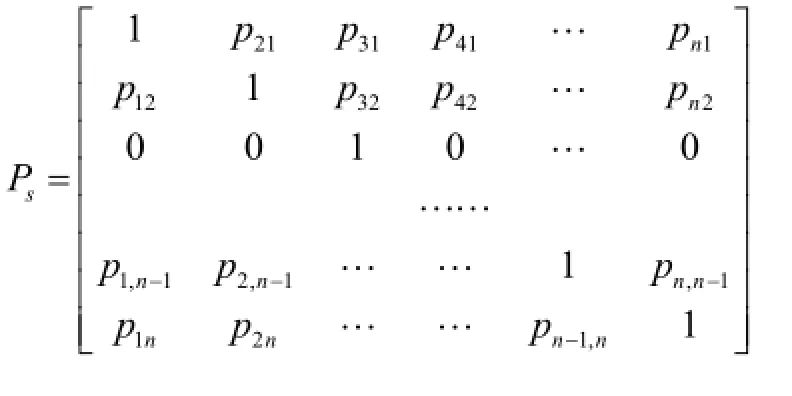
3 实例分析
3.1 罐区概况
选取图1中罐区某局部功能区进行实例分析。该储罐区有6个相同储罐,储罐容量20000m3,直径38m,储罐之间的中心距为58m,充装系数为0.85,存储介质为汽油。危险源辨识结果见表1。

表1 局部功能区重大危险源辨识与事故场景分析
3.2 火灾情形下罐区储罐失效概率分析
在罐A101发生火灾的情况下对罐A102和A104造成设备损害的概率为0.83、0.81。故该罐区的状态转移矩阵为:

相比于传统方法给出的罐区内各个储罐的失效概率为3.5×10-7,本文通过基于马尔科夫链的复杂网络事故传播模型得出的计算结果较小。不考虑罐区整体情况时单个储罐的失效概率要大于考虑相互作用后的该储罐的失效概率,即该罐区的运行情况为罐区内各个储罐提供了良性循环机制,有效遏制了个别储罐急剧恶化的趋势。当罐区整体运行情况不良时,这就会出现迭代不收敛的情况,即整体运行环境加速各个储罐的失效。此外,相比于风险叠加方法,本文建立的模型引入比例系数,充分考虑了罐区内储罐的个体性差异。而且,通过计算出来的比例系数,可以为罐区日常安全管理提供参考意见,如本文案例,在日常管理时需要侧重维护储罐A103和A104。
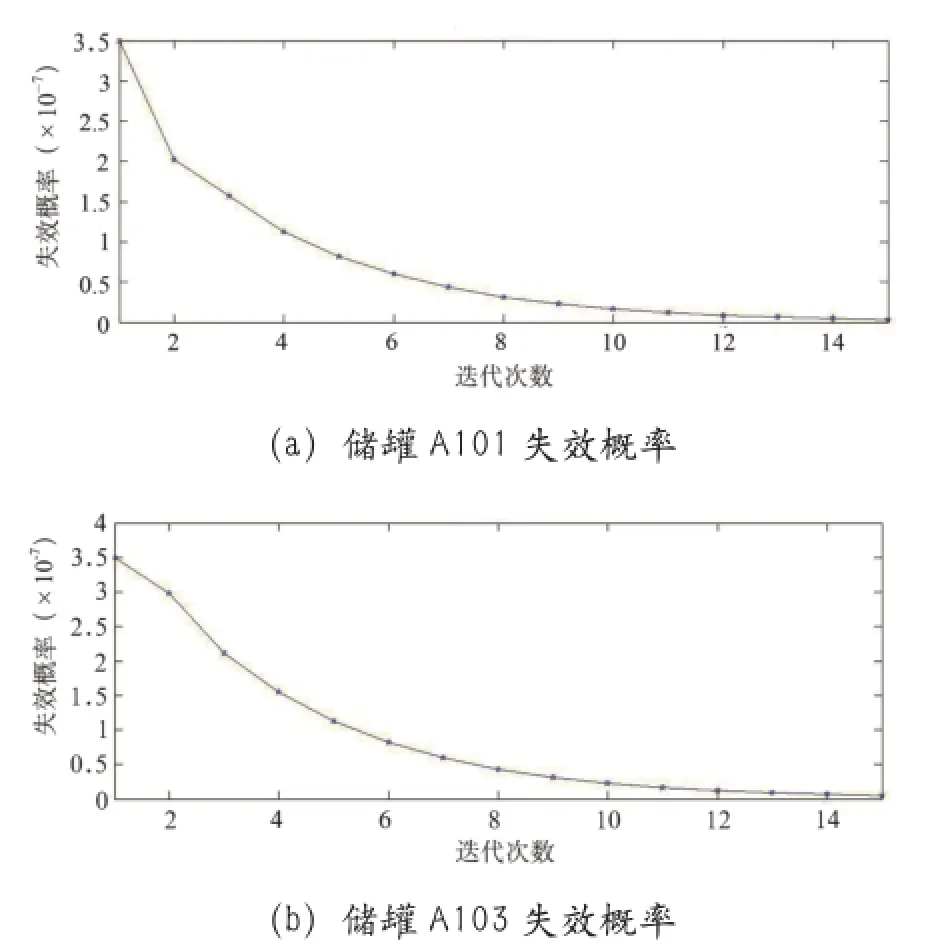
图3 储罐失效概率迭代结果
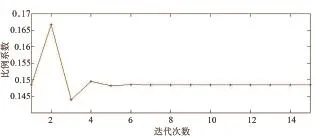
图4 储罐A101比例系数k1
4 结论
本文通过建立基于马尔科夫链的复杂网络事故传播模型,对罐区储罐进行失效分析,并进行实例分析,可以得出以下结论:
1)考虑罐区整体失效对单个储罐的影响,计算得出的储罐失效概率较传统方法脱离罐区整体计算的储罐个体失效概率更为有效,也更能反映储罐的真实风险。较传统的多米诺效应模型解决单一储罐对其他储罐的影响(即1-n问题),本文建立的模型可以有效解决了多个储罐之间的相互作用问题(n-n问题),计算结果较前一模型更客观。
2)引入单一储罐对罐区失效的贡献比例系数,充分考虑了储罐的个体差异性,解决了传统的风险叠加方法带来的计算值较真实值过大的问题。同时,通过模型求解出的比例系数,能够充分反映各个储罐对于罐区整体安全的重要程度,从而能够有效地指导罐区日常安全管理工作。
3)该模型对于整体运行情况良好罐区的失效概率分析比较适用(如本文实例分析),但对于整体运行情况不良的罐区还有待深入研究,模型还有待改善。
参考文献
[1] Valerio Cozzani. The assessment of risk caused by domino effect in quantitative area risk analysis[J].Journal of hazardous Materials,A127(2005):14-30.
[2] Valerio Cozzani. The quantitative assessment of domino effects caused by overpressure Part I. Probit models[J]. Journal of hazardous Materials,A127(2007):64-80.
[3] Valerio Cozzani. Prevention of domino effect:From active and passive strategies to inherently safer design[J].Journal of hazardous Materials,A139(2007):209-219.
[4] 陈国芳.化学工业园区危险性研究[D].沈阳:东北大学,2003.
[5] 吴丹.化学工业园区重大危险源分级及应急资源评估[D].沈阳:东北大学,2005.
[6] 戴雪松.重大事故多米诺效应研究[D].沈阳:东北大学,2005.
[7] 王洪德.基于网格划分及信息扩散的化工园区安全风险评价技术[J].系统工程理论与实践,2010(30):1286-1292.
[8] 王洪德.化工园区火灾爆炸风险网格矩阵叠加分析[J].系统工程理论与实践,2012,5(32):1143-1150.
[9] 李树谦.化工园区多米诺事故风险分析方法研究[J].安全生产与监督,2008,25(3):56-58.
[10] 杨国梁.大型原油储罐火灾多米诺效应概率计算模型及应用[J].中国安全生产科学技术,2013,8(9):130-134.
[11] 李尘.基于复杂网络理论的病毒传播模型研究[D].兰州:兰州理工大学,2013.
[12] 史明江.复杂网络中的病毒传播研究[D].上海:上海交通大学,2007.
[13](美)米尔斯切特等著.数学建模方法与分析[M].刘来福,杨淳等译.北京:机械工业出版社,2009:5.
[14] 周成.化工储罐区事故多米诺效应概率分析[J].石油化工设备,2010,5(39):31-36.
[15] 张新梅,陈国华.化工罐区爆炸碎片多米诺效应影响概率计算模型[J].化工学报,2008,11(59):2946-2953.
Research on the Failure Probability of Storage Tank Based on Markov Chain -Complex Network Accident Spread
Zonghui1Xufeiyun1Zhangyanbing2
(1. Mechanical Engineering Institute of Southeast University Nanjing 211189)
(2. Special Equipment Inspection & Research Institute of Nantong In Jiangsu Nantong 226000)
AbstractThrough the analysis of research methods of storage tank failure probability at home and abroad,this paper introduces the theory of complex network accident spread and Markov chain, and builds a complex network accident spread model based on Markov chain to solve the problem of n-n interaction among different tanks traditional methods involve rarely. After the analysis of an example, comparing the result of this model with traditional methods,it shows that this model can offer better suggestions for safety precaution.
KeywordsStorage tank failure probability Complex network accident spread Markov chain
中图分类号:X924.2
文献标识码:B
文章编号:1673-257X(2016)05-0023-04
DOI:10.3969/j.issn.1673-257X.2016.05.004
作者简介:宗辉(1991~),男,硕士,从事罐区安全评价研究工作。
收稿日期:(2015-11-09)
