基于棱镜扫描法的太阳光谱仪光谱定标

高震宇，方 伟，王玉鹏*，张 浩

1. 中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033 2. 中国科学院大学, 北京 100049

基于棱镜扫描法的太阳光谱仪光谱定标

高震宇1, 2，方 伟1，王玉鹏1*，张 浩1, 2

1. 中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033 2. 中国科学院大学, 北京 100049

为了标定扫描式棱镜太阳光谱仪的棱镜不同转动角度对应的中心波长和光谱带宽，利用了一种棱镜扫描方法对太阳光谱仪的光谱响应函数进行测量。该方法使用固定的单色光波长，控制棱镜转动实现单色光的像在探测器位置扫描，并通过坐标映射得到响应位置的光谱响应函数。文中根据光谱响应函数的定义，推导出棱镜扫描法与单色仪波长扫描方法波长定标原理上的等效性。之后分别以532 nm固体激光器和632.8 nm氦氖激光器为光源，使用棱镜扫描法测量太阳光谱仪对应波长位置的光谱响应函数，并以单色仪波长扫描法实验作为对比。实验结果表明，对于扫描式棱镜太阳光谱仪，棱镜扫描法测量的中心波长分别为531.86和632.67 nm，其准确度优于单色仪波长扫描法测得的531.39和631.97 nm。由于不受单色仪性能的限制，前者测量的光谱带宽值也优于后者。最后以汞灯为光源使用棱镜扫描法对太阳光谱仪进行了光谱定标实验，实现了特征光谱定标法结合棱镜扫描法对中心波长及光谱带宽的标定。该方法同样可以应用于扫描式光栅光谱仪以及单色仪的光谱定标。

光谱响应函数； 中心波长； 光谱带宽； 坐标映射

引 言

作为地球能量的主要来源，太阳辐射对全球能量平衡的至关重要[1]。并且由于大气、海洋以及不同地貌的陆地对太阳辐射的反射和吸收均具有不同的光谱选择性[2]，因此精确监测太阳光谱辐照度对地球气候研究和大气成分分析具有重要意义。太阳光谱仪是对太阳光谱辐照度进行连续定量化观测的仪器，准确、高精度的定标是保证其获得高质量监测数据的关键。太阳光谱仪的定标主要包括光谱定标和辐射定标，其中光谱定标是辐射定标的前提，且前者的定标精度将对后者的定标精度产生直接影响[3]。

光谱定标可视为求取光谱仪器各光谱通道的光谱响应函数(SRF)的过程，根据光谱响应函数可得到对应的中心波长和光谱带宽等特性。目前，光谱仪器常用的光谱定标方法主要有特征光谱定标法和单色仪波长扫描法[4]。其中，特征光谱定标法结构简单操作方便，在HRIS[5]，SCIAMACHY[6]等仪器的在轨定标过程中都有所应用，但该方法一般用于具有线性色散、高光谱分辨率的仪器定标，且只能标定中心波长，不能实现光谱带宽的标定[7]； 单色仪波长扫描法作为光谱定标常用方法，可同时实现宽光谱范围的中心波长和光谱分辨率的标定，具有定标精度高，可全光谱定标等优点[8]，在AVIRIS[9]，MODIS[10]等光谱成像仪器中得到应用。但由于实验中光谱定标结果实际是定标光源光谱分布函数与光谱仪器光谱响应函数共同作用的结果[11]，其定标精度受限于所用单色仪的精度和波长准确度。另外，对于色散元件转动式的光谱仪和单色仪，色散元件的转动定位精度及定位准确度也会使该类仪器光谱定标产生不确定度及误差项，这种不确定度与误差无法通过提高定标用单色仪的精度来消除。

针对上述情况，本文分析并使用了一种棱镜扫描方法对一架棱镜色散型太阳光谱仪进行光谱响应函数测量，该方法与单色仪波长扫描法过程不同但原理类似[12]，以固定波长的单色光为光源，利用转动棱镜的方法实现单色光的像在探测器位置扫描，并通过坐标映射测得相应位置的光谱响应函数。文中利用一组单色仪波长扫描法测量光谱响应函数实验作为对比，结果表明，对于文中所述太阳光谱仪，棱镜扫描法测量的中心波长与光谱带宽均与单色仪波长扫描法的结果相符且具有更好的准确度与精度。本文最后基于棱镜扫描法以汞灯为光源对太阳光谱仪进行了光谱定标，验证了棱镜扫描法光谱定标可行性。

1 棱镜扫描法定标原理

图1为自行研发并制造的棱镜型太阳光谱仪的结构原理图，由入射狭缝、Fery棱镜、转动电机、出射狭缝和光电二极管探测器组成。该装置狭缝和探测器固定，通过电机控制棱镜转动获得工作光谱范围内的全光谱信息。棱镜的转动角度信息通过读取参考光路中的线阵CCD响应获得，并将线阵探测器像元编号作为角度代码。该太阳光谱仪分为三个通道对300～2 500 nm光谱范围太阳光进行监测，光谱分辨率为1～42 nm。本文主要针对300～1 000 nm通道进行分析讨论。

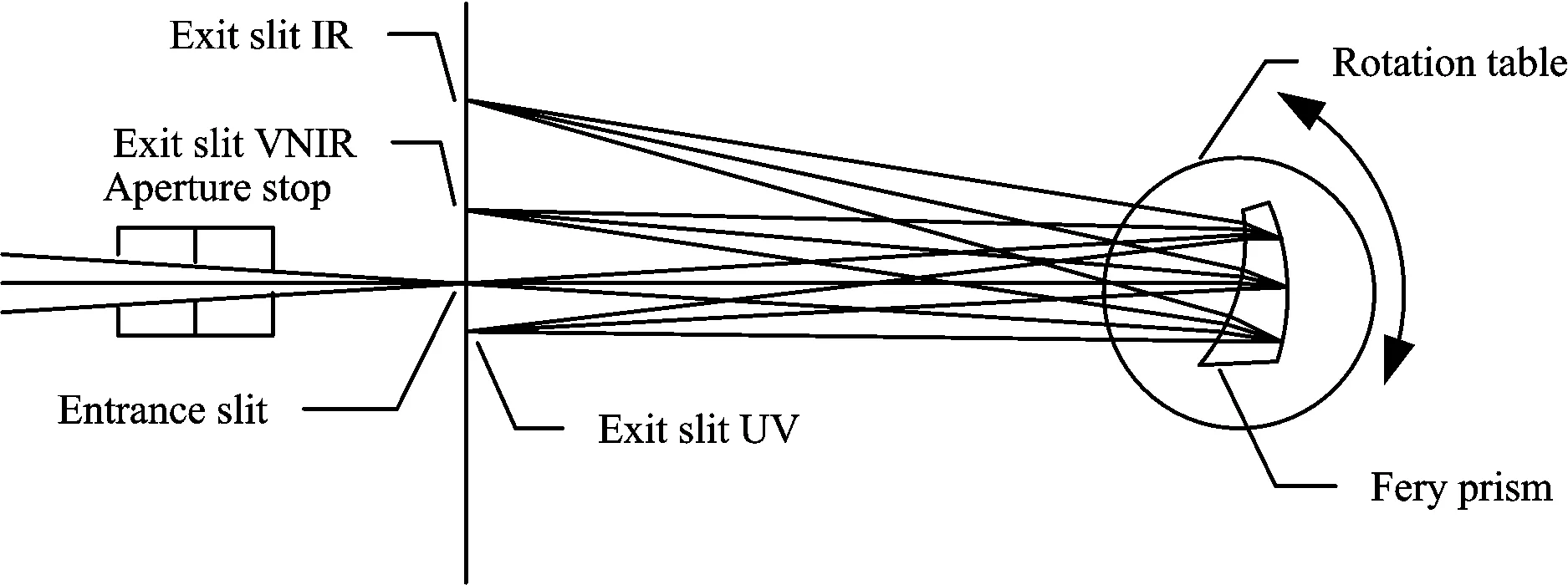
图1 棱镜太阳光谱仪光路结构

上述系统中，探测器的响应是探测器在对应位置接收到的所有波长能量的叠加[13]，光谱响应函数即为光电二极管探测器对这些不同波长单色光能量响应随波长分布的函数。针对该系统，单色仪波长扫描法需要固定太阳光谱仪的分光棱镜在被测波长位置，通过连续改变单色仪输出光波长，测量并记录探测器输出则获得该波长位置处的光谱响应函数。由于不同波长对应的狭缝像沿着色散方向分布，此过程即为不同单色波长的像函数对固定的探测器的平移扫描。在所测的中心波长附近一定程度范围内，像差对单色像能量分布影响有限，可以考虑不同波长单色光的像能量分布相同，仅在色散方向上有位移。则像函数可以表示为

(1)

式中，y为像面坐标，λ为波长，λ0为棱镜固定位置对应的中心波长，Δλ为波长与中心波长λ0的波长差，Δy为波长为λ的像中心距探测器中心的平移量，Δλ与Δy一一对应。光谱响应函数可表示为

(2)

式中，s(y)为出射狭缝函数。

现在固定输入的单色光波长，通过电机控制分光棱镜旋转，使单色光的狭缝像在探测器附近移动完成扫描。此过程单色像能量分布变化可以忽略，仅在色散方向产生位移，可以等效为固定棱镜，改变单色光波长的扫描过程。该过程可以看作单色光的狭缝像固定，控制出射狭缝平移完成扫描。此时光谱响应函数可表示为

(3)

由式(2)和式(3)可见，针对本文所述的太阳光谱仪，在假设中心波长附近的小光谱范围内单色像函数无明显变化时，固定输入单色光波长的棱镜扫描法具有和单色仪波长扫描法相同的推导结果，因此可以考虑上述两种方法等效。事实上，在中心波长的光谱带宽的范围内单色像函数的变化很小，允许上述假设成立。如图2所示为根据图1中太阳光谱仪点扩散函数(PSF)模拟[14]的太阳光谱仪632.8 nm的单色光像函数与620 nm以及645 nm单色光像函数的相对偏差，可知最大相对偏差小于1%。

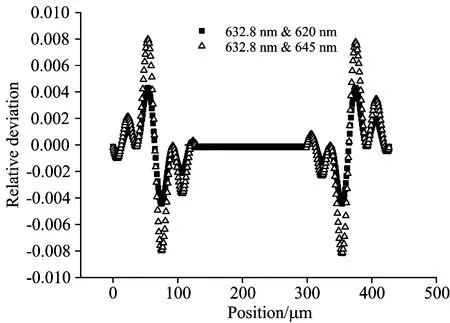
图2 632.8 nm与附近波长像函数相对偏差

2 棱镜扫描法测量光谱响应函数

根据棱镜扫描法的定标原理，针对棱镜太阳光谱仪，搭建的定标装置示意图如图3所示，由定标光源、石英会聚透镜、光纤、反射式抛物面准直镜构成。定标光源根据需要可以是单色仪出射的单色光、谱线灯或者激光，其中激光额外加入一片毛玻璃用来去偏振和匀光，将经过毛玻璃作用后出射的光作为定标光源。石英会聚透镜和反射式抛物面准直镜与光纤之间通过SMA905接口连接，并且可以通过微调接口处的距离来调节出射光的发散角。

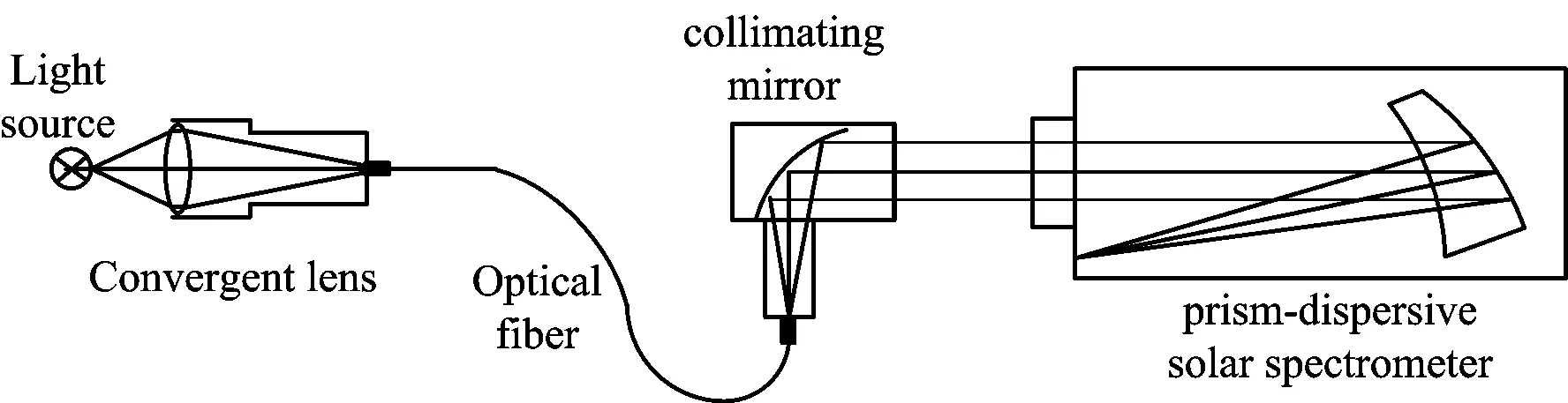
图3 棱镜扫描法定标装置示意图

使用棱镜扫描法对太阳光谱仪532和632.8 nm处光谱响应函数进行测量，定标光源分别选择532 nm的固体激光器和632.8 nm的He-Ne激光器，二者的光谱带宽均远小于0.1 nm，与单色仪出射的单色光相比，可以忽略定标光源本身光谱带宽对光谱响应函数测量的影响，且波长准确度和功率稳定性好。分别在532和632.8 nm对应的棱镜位置处，控制棱镜精密转动完成扫描并记录棱镜转角对应的响应值，得到探测器响应随太阳光谱仪棱镜转角变化的曲线，其中棱镜转角以一块线阵CCD像元编号表示。对上述测量结果进行一次坐标映射，将探测器像元坐标映射为波长坐标，则可以获得仪器的光谱响应函数。此过程可以通过光谱仪光学系统的相关参数模拟获得，但加工装调过程中引入的像差无法包含在模拟结果之中。因此本文采用实验方法，测量多组被测中心波长附近的波长的光谱响应曲线，分别拟合并记录波长对应的探测器像元，最后通过多项式拟合获得波长与探测器像元的对应关系。对532和632.8 nm波长附近分别进行上述测量，并对数据进行三次多项式拟合，可得对应532和632.8 nm的拟合结果分别为

y=-28 949.27+20.27x-4.67×10-3x2+3.61×10-7x3

y=-77 827.24+47.54x-9.64×10-3x2+6.55×10-7x3

拟合结果对应的拟合残差如图4所示，其中代表横坐标的棱镜转动角和波长的对应关系基于三次多项式拟合，因此并非是线性的。由图可知，在532和632.8 nm附近位置拟合残差分别小于0.06和0.09 nm。

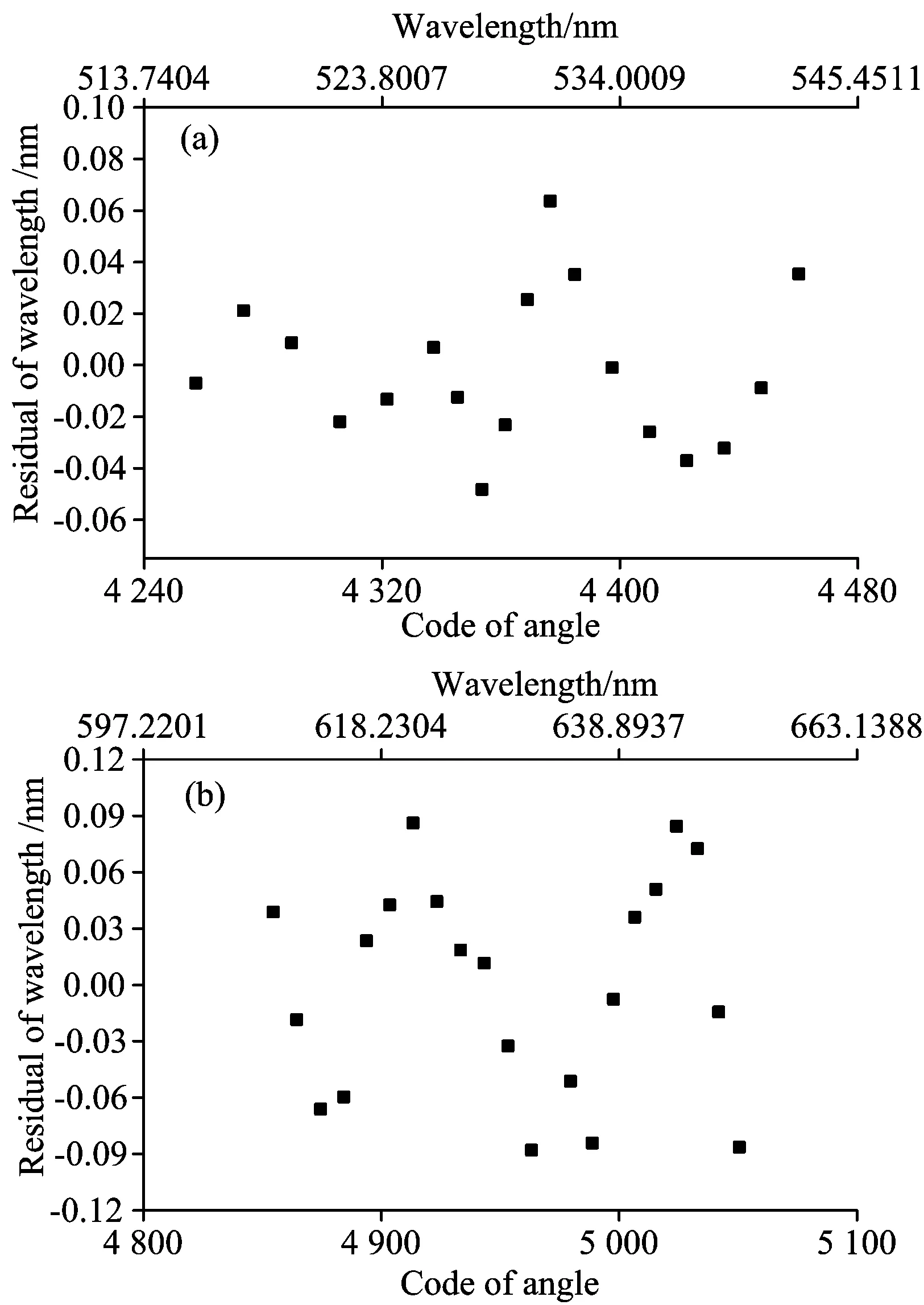
图4 多项式拟合对应的拟合残差

根据拟合结果对棱镜扫描法的直接测量的探测器响应随棱镜转角变化曲线进行坐标映射，将角度坐标映射为波长坐标后获得光谱响应函数曲线，532和632.8 nm波长位置的光谱响应函数如图5所示，其中波长坐标与探测器像元坐标的对应关系由上文所述的非线性拟合获得。对两波长的光谱响应函数分别进行高斯函数拟合，可得实验测量的中心波长分别为531.86和632.67 nm，对应的函数FWHM值即光谱带宽分别为9.39和15.14 nm。

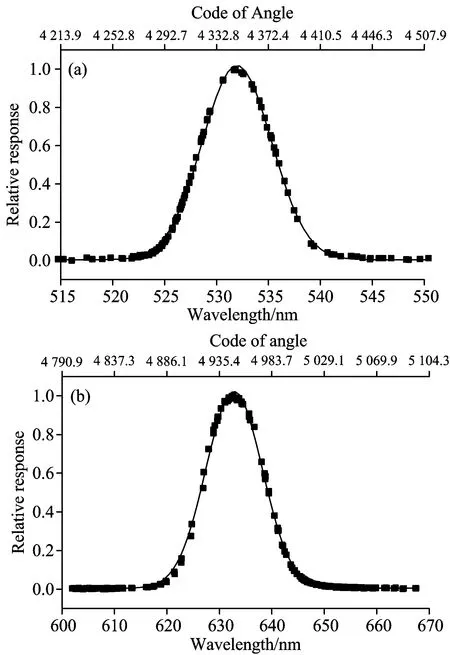
图5 棱镜扫描法测量的太阳光谱仪光谱响应函数

与棱镜扫描法作对比，使用单色仪波长扫描法对太阳光谱仪532和632.8 nm波长位置的光谱响应函数进行测量，实验中使用高功率卤钨灯作为光源，实验所用单色仪最优光谱分辨率为0.1 nm，准确度为0.2 nm，重复性为0.1 nm。测量结果如图6所示，其拟合后的高斯曲线中心波长分别为531.39和631.97 nm，对应的光谱带宽为9.53和15.36 nm。

对比上述两种方法的实验结果，可知对于文中所述的棱镜转动式光谱仪，棱镜扫描法的结果与单色仪波长扫描法的结果相符，且对中心波长的测量更具优势。因为单色仪波长扫描法测量的中心波长会受到拟合过程以及所用单色仪的准确度和重复性影响，除此之外，对于本文中的色散元件扫描式的光谱仪，使用单色仪波长扫描法测量光谱响应函数时需要固定色散元件在定标波长位置处，色散元件实际固定位置与标称位置之间的误差也对中心波长的测量产生直接影响。而棱镜扫描法是使用激光作为光源，光源本身造成的偏移可以忽略，并且该方法不存在色散棱镜固定位置的误差，因而避免了相应的对不确定度及准确度的影响，其不确定度主要来自拟合过程和坐标映射过程。在光谱带宽测量方面，由于激光光源本身带宽引入的影响几乎可以忽略，而单色仪出射光的光谱带宽会对标定的光谱带宽产生影响[15]，因此单色仪波长扫描法测得光谱带宽数值大于棱镜扫描法测的数值。

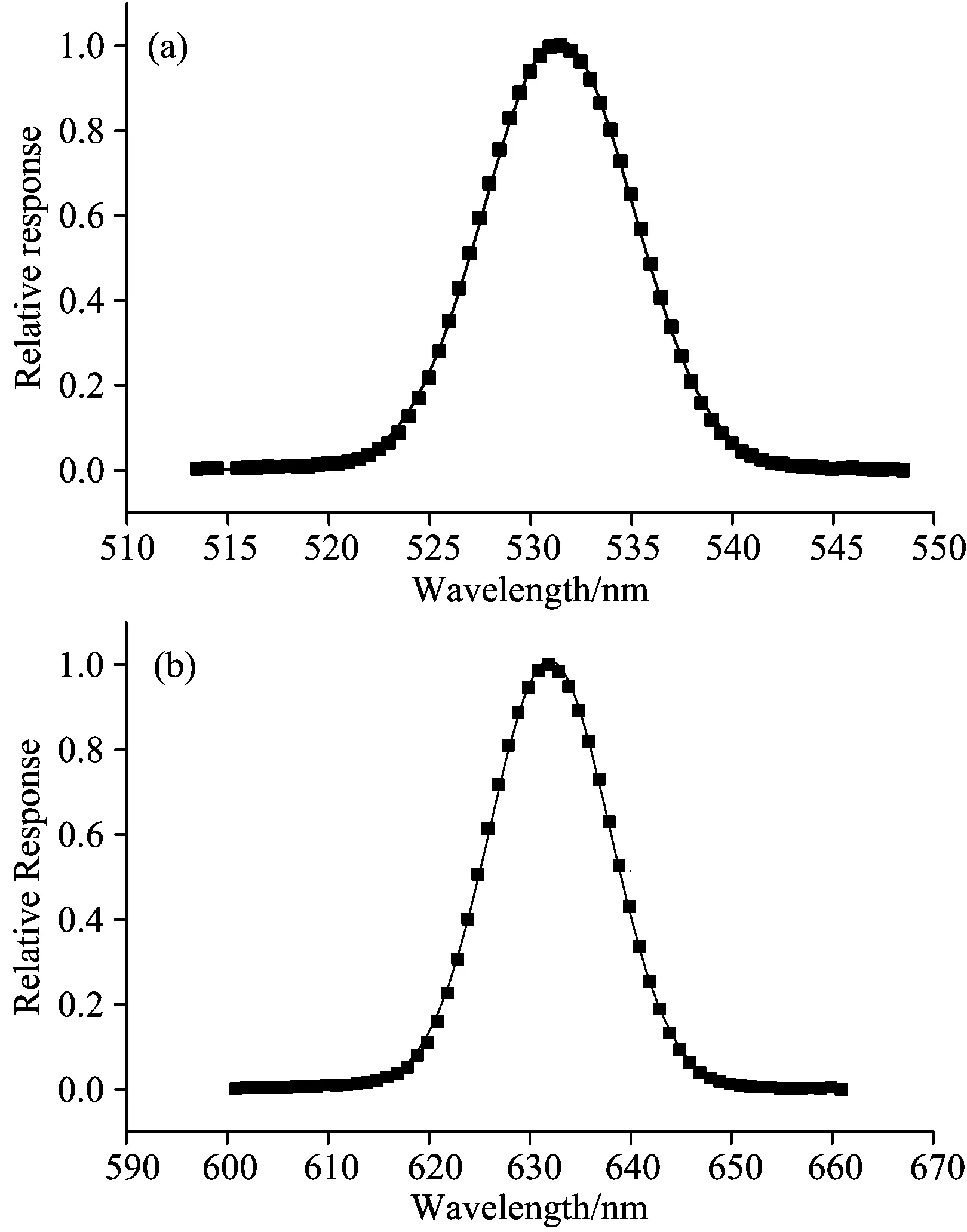
图6 单色仪波长扫描法测量太阳光谱仪光谱响应函数

3 棱镜扫描法的光谱定标

传统的特征光谱定标法只能实现中心波长的标定，无法标定光谱带宽。但是应用汞灯等具有特征谱线的光源，结合棱镜扫描法可以同时实现中心波长和光谱带宽的标定，并且由于特征谱线具有较高的稳定性和几乎可以忽略的光谱带宽，与单色仪波长扫描法相比可以减少波长偏移和光源本身光谱带宽对光谱定标的影响，提高定标的精度与准确度。

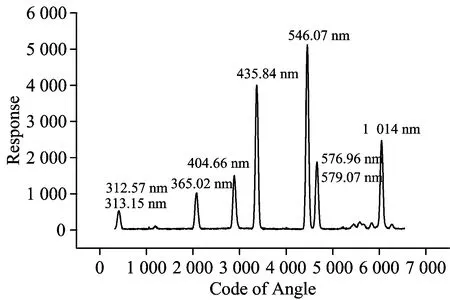
图7 太阳光谱仪对汞灯光源精细扫描响应曲线

太阳光谱仪对汞灯光源光谱进行精细扫描的响应曲线如图7所示，图中响应峰值对应波长由太阳光谱仪测量波长与色散元件角度对应关系结合汞灯特征谱线推断获得。由于太阳光谱仪光谱分辨率有限，图中312.57，313.15 nm以及576.96，579.07 nm无法有效分开，因此不作为有效数据。对图中每一个谱线的响应数据进行高斯函数拟合，可以获得与该谱线波长对应的色散元件转动角，将这些定标数据进行多项式拟合，则实现太阳光谱仪在365.02～1 014 nm波段的波长定标。另外对拟合好的高斯函数进行坐标映射，求对应波长位置的光谱响应函数，进而获得对应波长位置的光谱分辨率。以汞灯为光源的光谱定标数据如表1所示。对表中光谱分辨率数据进行多项式拟合，可得太阳光谱仪365.02～1 014 nm波段范围内光谱分辨率变化曲线如图8所示，图中数据点为实验测试获得，曲线是各数据点经三次多项式拟合而成。

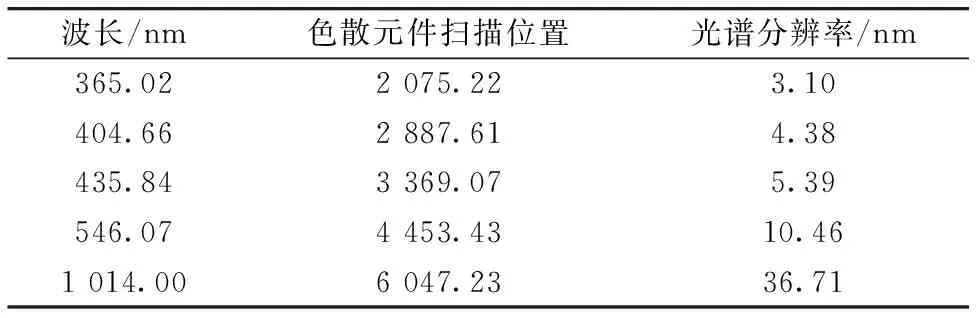
表1 汞灯光源光谱定标有效数据

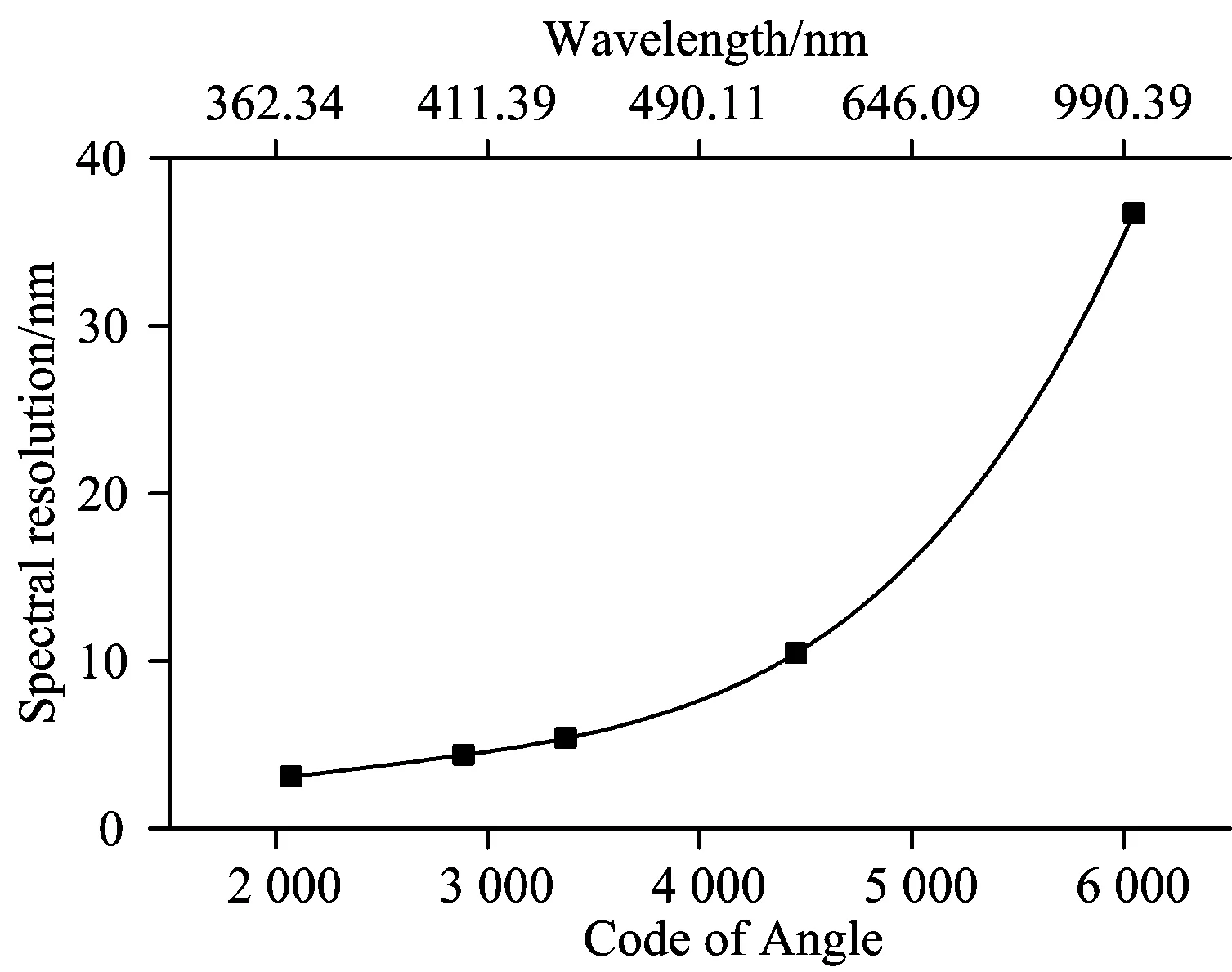
图8 太阳光谱仪365.02～1 014 nm光谱分辨率曲线

由上述过程可见棱镜扫描法可以实现文中太阳光谱仪的光谱定标，但由于汞灯在波长范围内特征谱线数量较少，因此上述光谱定标过程数据量较小，对此可以将氖、氩、氙等光谱校准灯组合使用，则特征谱线从紫外到近红外均有分布，结合棱镜扫描法可应用于宽光谱范围的色散元件扫描式光谱仪器的光谱定标。

4 结 论

针对棱镜扫描式太阳光谱仪，分析并使用了棱镜扫描法测量其光谱响应函数，并设置了单色仪波长扫描法测量光谱响应函数作为对比实验。对比结果表明，对于棱镜扫描式光谱仪，棱镜扫描法的测量结果与单色仪波长扫描法测量结果相符，并且由于不受单色仪性能限制，在测定中心波长和光谱带宽方面相比单色仪波长扫描法具有更好的准确度。最后，本文以汞灯为光源利用棱镜扫描法对太阳光谱仪进行光谱定标，验证了棱镜扫描法光谱定标的可行性。对于色散元件转动式的光栅光谱仪和单色仪，将本文中的棱镜扫描改为色散元件扫描，上述方法同样有效。

[1] LIU En-chao, ZHENG Xiao-bing, LI Xin, et al(刘恩超，郑小兵，李 新，等). Opt. Precision Eng.(光学精密工程), 2013, 21(3): 608.

[2] ZHANG Hao, FANG Wei, YE Xin, et al(张 浩，方 伟，叶 新，等). Acta Optica Sinica(光学学报), 2013, 33(2): 178.

[3] ZHENG Yu-quan(郑玉权). Opt. Precision Eng. (光学精密工程), 2010, 18(11): 2347.

[4] ZHANG Chun-lei, XIANG Yang(张春雷，向 阳). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2012, 32(1): 268.

[5] Barry P S, Shepanski J, Segal C. SPIE, 2002, 4480: 231.

[6] Mager R, Fricke W, Burrows J P. SPIE, 1997, 3106: 84.

[7] QI Xiang-dong, HAN Peng-peng, PAN Ming-zhong, et al(齐向东，撖芃芃，潘明忠，等). Opt. Precision Eng. (光学精密工程), 2011, 19(12): 2870.

[8] JIN Hui, JIANG Hui-lin, ZHENG Yu-quan, et al(金 辉，姜会林，郑玉权，等). Chinese Journal of Luminescence(发光学报), 2013, 34(2): 235.

[9] Vane G, Chrien T G, Miller E A, et al. SPIE, 1987, 834: 91.

[10] Amold G T, Fitzgerald M F, Grant P S, et al. SPIE, 1996, 2820: 56.

[11] WANG Ming-zhi, YAN Lei, YANG Bin, et al(王明志，晏 磊，杨 彬，等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(8): 2280.

[12] Harder J W, Thuillier G, Richard E C, et al. Solar Physics, 2010, 263(1): 3.

[13] Mouroulis P, Sellar R G, Wilson D W, et al. Optical Engineering, 2007, 46(6): 063001.

[14] Mouroulis P, Green R O. SPIE, 2007, 6667: 66670.

[15] SUN Ci, Bayanheshig, CUI Ji-cheng, et al(孙 慈，巴音贺希格，崔继承，等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(8): 2289.

*Corresponding author

(Received May 4, 2015; accepted Sep. 20, 2015)

Spectral Calibration of a Solar Spectrometer Based on the Prism-Rotating Method

GAO Zhen-yu1, 2, FANG Wei1, WANG Yu-peng1*, ZHANG Hao1, 2

1. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China 2. University of Chinese Academy of Sciences, Beijing 100049, China

In order to calibrate the corresponding center wavelength and bandwidth to the prism’s rotating angle of a scanning prism-dispersive solar spectrometer, a prism-rotating method to measure the spectral response function (SRF) of the solar spectrometer is suggested. The measuring process is as follows. With the wavelength of monochromatic light invariant, the prism is rotated for scanning the monochromatic image at the location of detector. Then the spectral response function is obtained by mapping the coordinate in position to the coordinate in wavelength. At first in this paper, by analyzing the definition of SRF, the conclusion is deduced that the prism-rotating method is equivalent to the wavelength-scanning method in practice. Then the 532 nm solid-state laser and 632.8 nm He-Ne laser are used as light source. The measurement of SRF of the solar spectrometer based on prism-rotating method is performed. A measurement of SRF with wavelength-scanning method is also performed to be used as a comparison. Experimental results indicate that the center wavelength of the scanning prism-dispersive solar spectrometer measured with prism-rotating method is 531.86 and 632.67 nm respectively. On the other hand, the result is 53139 and 631.97 nm with wavelength-scanning method, which is less precise than the result of prism-rotating method. The values of bandwidth measured with prism-rotating method are also more precise than the latter owing to avoiding the performance deficiency of monochromator. At last, using mercury vapor lamp as light source, an experiment for spectral calibration of the solar spectrometer with prism-rotating method is performed. The values of center wavelength and bandwidth are both achieved with the method combining the prism-rotating method and chracteristic spectrum. This method can also be used to calibrate the monochromator and the grating-dispersive spectrometer whose grating is rotatable.

Spectral response function (SRF); Center wavelength; Spectral bandwidth; Coordinate mapping

2015-05-04，

2015-09-20

国家自然科学基金项目(41474161)资助

高震宇，1988年生，中国科学院长春光学精密机械与物理研究所博士研究生 e-mail: lnsygzy@126.com *通讯联系人 e-mail: wangyp@ciomp.ac.cn

TH774

A

10.3964/j.issn.1000-0593(2016)06-1930-06