一种基于改进累积方差百分比的红外高光谱数据降噪方法
2016-07-12高太长李书磊
黄 威,高太长,刘 磊,李书磊
解放军理工大学气象海洋学院, 江苏 南京 211101
一种基于改进累积方差百分比的红外高光谱数据降噪方法
黄 威,高太长*,刘 磊,李书磊
解放军理工大学气象海洋学院, 江苏 南京 211101
降低红外高光谱观测数据中的噪声水平是提高温湿廓线反演精度和反演稳定性的重要环节。采用主成分分析法降噪时,最优主成分个数k的选择一般是根据统计和经验的方法确定。统计的方法大都是根据累积方差百分比法,通过人为设定累积贡献率阈值确定最优主成分个数,使得该方法具有较大的主观性和随意性;经验的方法则需要实时的等效噪声光谱(NESR)数据做标准化处理将非均匀噪声转化为高斯分布,而实时的NESR数据在很多情况下不易获取。针对上述问题,提出了一种基于改进累积方差百分比的主成分降噪方法,通过迭代计算选取不同主成分时重构光谱辐射与模拟光谱辐射的偏差来计算累积贡献率阈值,根据阈值确定最优的主成分个数。该方法解决了确定累积贡献率阈值主观随意性的问题,并且不需要实时的NESR数据做标准化处理。根据物理反演结果分析了数据的标准化对降噪的影响,结果表明,标准化对降噪效果的影响很小,由标准化造成的k值计算误差对降噪效果的影响更大。利用该方法对2011年4个季度中具有代表性的数据做降噪处理,反演的温度廓线均方根误差相比于经验公式法在0.32~3 km高度上提高了约0.1 K,与利用等效噪声光谱标准化后的降噪数据的反演结果精度相当。在无法获取等效噪声光谱数据情况下,该方法可以客观合理地对地基红外高光谱数据进行降噪。
高光谱降噪;累积方差百分比;标准化;牛顿非线性迭代
引 言
在过去的几十年中,科学家们研发了多种新的仪器来探测大气的温度、湿度和风的信息。其中,地基红外高光谱分辨率傅里叶变换光谱仪(如美国威斯康辛大学研发的AERI,atmospheric emitted radiance interferometer)能够提供分辨率小于1 cm-1的下行红外辐射数据[1],包含有丰富的大气廓线、气溶胶、云以及其他重要的大气参数信息,在探测边界层大气温湿廓线方面具有独到的优势[2]。但是探测通道的增加,也使得数据中的冗余信息和噪声信息增多[3]。在利用观测数据反演大气状态参量信息时,由于辐射传输方程的高度非线性,使得高光谱红外辐射中的噪声在反演时被放大,导致反演精度的下降甚至不稳定[4]。因此降低观测数据中的噪声水平是提高反演精度和反演稳定性的重要环节。常用的降噪方法大都是基于平滑的方法进行处理,虽然平滑的方法可以去除观测数据中的高频噪声,但是会牺牲观测数据的时间分辨率并且平滑掉一部分的有效信号,造成信号失真[5]。同时,为捕捉仪器上空大气的对流运动,往往需要增加仪器探测的时间分辨率,此时通过滑动平均来提高观测数据的信噪比的方法不再适用。
目前,对于高光谱数据的降噪常用主成分分析法[6]。该方法利用光谱通道之间的高度相关性来降低观测数据中的非相关噪声[7],从而提高辐射光谱的信噪比。相比基于平滑的降噪方法,主成分降噪法能够保留观测数据中绝大部分的有效信息,并且不影响其时间分辨率和光谱分辨率。利用主成分分析法降噪最先应用在星载遥感探测器上并获得了快速的发展,如扫描高分辨率干涉仪(S-HIS)和大气红外探测器(IASI)[8];Turner第一次将主成分降噪方法应用在地基红外高光谱遥感探测器AERI上,对美国大气辐射测量(atmospheric radiation measurement,ARM)计划中的辐射光谱数据进行降噪处理,取得了较好的效果[7]。
利用主成分分析法降噪首要的问题是确定最优的主成分个数k[5],使得重构数据中的噪声显著降低,同时又保留了观测数据中绝大部分的有效信息。目前,还没有一种解析的方法给出准确的k值,在实际应用中大都是根据统计和经验的方法来确定。其中,应用较多的是累积方差百分比法,该方法通过对历史观测辐射数据做SVD分解,计算分解得到的特征值的累积贡献率,通过给定一个接近于1的阈值来确定k的大小。但是该方法阈值的确定都是人为地设定,具有较大的主观性和随意性,从而限制了该方法的应用[7]。
Turner将化学分析领域确定最优主成分个数的方法引入到光谱降噪中,利用经验公式计算混合在真实信号中的相关噪声,由于该噪声的大小与使用的主成分个数有关,相关噪声达到最小时对应的主成分个数即为最优的k值[7]。当观测数据的噪声满足高斯分布时,经验公式法的计算结果较好,此时需要利用NESR数据对观测数据做标准化处理将其中的噪声均匀化。NESR是辐射定标公式的虚部[9]
(1)
其中C是观测得到的复数光谱,通过对干涉图像做傅里叶变换得到;B是由黑体的辐射率光谱和普朗克公式计算得到,但是这些原始数据很多情况下很难获取,导致无法将原始数据中的噪声转化为高斯噪声,此时利用该方法计算的最优主成分个数就会出现误差。
根据以上两种方法的优缺点,提出了一种改进的累积方差百分比法(Improved PCV),该方法基于模拟辐射数据计算累积方差百分比阈值,通过阈值确定最优主成分个数,无需利用实时的NESR数据。首先,介绍了主成分分析法降噪方案,并阐述了利用Improved PCV计算最优主成分个数的具体过程;然后分析了数据的标准化以及最优主成分个数计算误差对反演的影响;最后,利用Improved PCV方法对2011年四个季度晴空辐射观测数据进行了降噪处理,并将该方法的反演结果和经验公式法的结果进行了对比。
1 Improved PCV降噪方案
Improved PCV降噪方案是将模拟辐射光谱作为大气的“真值”[3],通过迭代计算选取不同主成分时重构辐射与模拟辐射的偏差来确定PCV法的阈值。选用美国大气和环境研究公司开发的逐线积分辐射传输模式(LBLRTM)计算模拟辐射光谱。LBLRTM是一种精确、灵活、高效的辐射传输模式[10],在实际的计算中,该模式的计算精度接近0.5%。算法造成的计算误差是谱线参数和线型误差的五分之一左右,具有较高的精度。在此条件下,该方法的流程图如图1所示,具体步骤如下:
第一步: 根据总天空成像仪(total sky imager,TSI)获取的全天空云图,从历史观测辐射和探空数据中挑选出Mtr个晴空辐射光谱和温湿廓线,组成晴空数据样本集。计算样本集中观测辐射协方差矩阵M,并做SVD分解
M=URVT
(2)
其中R是包含Nc个特征值λ的对角矩阵,Nc是观测辐射中通道个数,U的列是与R的特征值对应的特征向量,又称为主成分。
第二步: 从矩阵U中选取前q个主成分组成矩阵P,根据公式
(3)
计算出投影系数,其中i=1,…,Mtr,j=1,…,q。
第三步: 投影系数乘以矩阵P的转置,将其重构到辐射空间
(4)
其中,i=1,…,Mtr;j=1,…,Nc。
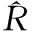
(5)
l从1到Nc逐渐增加,对应的偏差值随着选用主成分个数的变化而改变,当偏差达到最小值时对应的l即为该条观测辐射R的最优主成分个数k。
第五步: 计算观测样本集中每条观测辐射的最优k值并利用公式
(6)
计算出PCV大小,对PCV取平均得到阈值。
第六步: 根据阈值计算出最优主成分个数k,对于一组新的观测数据,重复第二和第三步步骤,即可实现观测数据的降噪。

图1 降噪方案流程图
2 降噪效果评估
2.1 数据简介
反演使用的辐射数据是2010年和2011年ARM计划中南部大平原(southern great plains,SGP)站点的AERI观测的辐射数据。AERI是由美国威斯康辛大学研发的地基高光谱探测仪,它通过两个探测器观测520~3 020 cm-1的干涉图像,根据傅里叶变换将干涉图像转化为辐射光谱。之后利用高温黑体和环境黑体对观测辐射做定标处理,能够获得观测周期为8 min精度达到1%的下行红外辐射数据[9]。
但是,由于仪器上方的大气活动以及视场镜的转换等因素导致观测数据中包含有较多的误差,这部分误差大致包括两个部分: 仪器噪声和系统偏差。前一部分可以通过主成分分析等滤波方法进行抑制;对于后者,一般通过计算晴空条件下观测辐射光谱和模拟辐射的偏差获取[3],在降噪之前减去这部分系统偏差即可。其中模拟辐射光谱的计算是将与观测辐射对应的探空廓线放入逐线积分辐射传输模式LBLRTM计算得到,通过SGP站点的TSI图像从2011年的辐射数据中挑选了105个晴空样本数据,利用LBLRTM计算出这两年的晴空模拟辐射,通过计算其与观测辐射偏差的平均值就可以得到仪器的系统偏差。
2.2 评估方法
对于地基红外高光谱数据降噪而言,其目的是减小在反演过程中因误差反传造成的反演偏差和不稳定。因此,根据物理反演温度廓线的精度来评估不同去噪方法的降噪效果是比较客观合理的。其中,温度廓线的反演方法采用牛顿非线性迭代法,反演的波段采用的是612~712和2 223~2 260 cm-1两个CO2吸收带[2]。
牛顿非线性迭代法的求解形式如下[11]
(Ym-Y(Xn)+Fn(Xn-X0))
(7)
其中Ym是观测辐射向量,X是要反演的温度廓线,X0是初始温度廓线,Y(X)是利用辐射传输模式计算的辐射值,γ是正则化算子,E是观测误差协方差矩阵,B是背景误差协方差矩阵。对于正则化算子γ,采用AERIoe中的向量法,取为[1000 300 100 30 10 3 1][12]。
在观测辐射数据中,和温度有关的信息绝大部分在2 km以下,因此牛顿非线性迭代法的反演高度一般不超过3 km;由于使用的数据位于SGP站点,其海拔高度为320 m,所以反演温度廓线的高度范围在0.32~3 km之间,在反演时将该部分大气按照垂直分辨率由高到低的方式分为19层。
2.3 降噪结果分析
(1)NESR对降噪效果的影响
在无法获取实时的NESR数据情况下,此时无法做标准化处理。而数据的标准化会改变观测数据中的噪声分布,对温度廓线的反演结果和最优主成分个数的确定都会产生影响。如果标准化对反演的结果影响较大,在不做标准化的条件下,无论k值计算多么精确,都无法提高大气温度廓线的反演精度。
采用控制变量的方法对标准化的影响程度进行分析,首先,通过固定所选取的主成分个数k分析数据的标准化对反演精度的影响。其中k是在标准化的条件下通过经验公式法计算因素指标函数(factor indicator function,IND)
(8)
它表示利用k个主成分降噪后保留在观测数据中的噪声,可见IND值越小,降噪效果越好,最小的IND值对应的k即为最优的主成分个数[7]。图2是利用2010年和2011年的晴空辐射数据计算得到的不同k值的IND图像,其中Nc表示所选用波段的通道个数。如图中星号所示,在k取12时IND值达到了最小,表明在选用12个主成分降噪时残留在观测数据中的噪声最小,此时k=12即为最优的主成分个数。而在不进行标准化的情况下,利用经验公式法对2010年和2011年的晴空辐射数据做降噪处理,在k=8时IND取得最小值,相比于标准化情况下的k=12偏小。

图2 k取1到Nc时的IND值
接下来利用牛顿非线性迭代法分析标准化对降噪以及最优主成分个数选择的影响。选取2011年9组具有代表性的数据进行分析: 首先,固定k值等于12,分析做标准化处理和不做标准化处理时的反演结果;其次,k分别取为8和12,在进行标准化的条件下计算二者的降噪效果。图3是取不同k值以及不同标准化条件下的温度廓线反演结果图像,其中红色实线表示标准化时取k=12反演的温度廓线的均方根误差(root-mean-square error,RMSE),黑色实线表示标准化时取k=8的反演结果,蓝色星号线表示不做标准化的情况下k取12时的反演结果。可以看出,观测数据的标准化本身对反演结果的影响较小,而由标准化造成的主成分个数计算不准确对反演结果影响更大。

图3 数据标准化对温度廓线反演精度的影响
(2)降噪方法结果分析
在没有NESR的情况下,采用Improved PCV法确定最优的主成分个数。选取2011年SGP站点27个晴空观测辐射和温湿廓线作为样本集,利用LBLRTM计算与之对应的模拟辐射,从而得到了27个观测样本的最佳主成分个数k和累积方差百分比,取其累积方差百分比的平均值得到阈值0.999 945 971。利用该方法对2011年10月20日的温度廓线进行反演,在上述阈值条件下其最优主成分个数取为27,图4是利用该方法对2011年10月20日17:30分的数据做降噪处理后在0.32~3 km的高度上温度廓线的反演结果,其中黑色实线为初始温度廓线,红色实线表示探空数据,蓝色实线为去除系统偏差后的反演结果,黑色带星号实线表示利用Improved PCV方法的反演结果。可以看出,降噪后的温度反演精度要明显优于不做降噪处理的反演结果,表明该方法能够很好地降低观测数据中的噪声水平。

图4 利用改进PCV方法降噪的反演结果
为验证该方法的可靠性,对上述的9组晴空观测辐射数据利用主成分分析法做降噪处理,其中阈值的选择分别根据经验法和累积方程百分比法获取。结果如图5所示,其中实线表示在标准化条件下利用经验公式法降噪后反演的温度廓线RMSE值,虚线表示不做标准化时利用Improved PCV法降噪后的反演结果。除0.5~1 km高度外,利用PCV方法的降噪结果与标准化条件下经验公式法的反演精度相当,相比于不做标准化时的经验公式法精度提高约0.1 K。因此在无法获取准确的NESR数据时,可以利用Improved PCV阈值确定方法对观测数据做降噪处理。

图5 经验公式法与Improved PCV方法反演的
Fig.5 The RMSE of the retrieval temperature profiles of the factor indicator function method and the Improved PCV method
3 结 论
在高光谱数据降噪中,主成分分析法将高度相关的观测数据分解,通过选取一定个数的主成分重构到辐射空间以达到去噪的目的。在观测数据中的噪声满足高斯分布的条件下,利用经验公式法计算的最优主成分个数能够很好地降低噪声水平。但是很多情况下无法获取准确的NESR数据,导致无法通过标准化步骤将噪声转化为高斯分布。通过分析标准化对物理反演结果和最优主成分个数计算的影响,提出了一种利用模拟辐射光谱确定阈值的累积方差百分比法,并利用牛顿非线性迭代反演法评估降噪效果,拓展了PCA方法的使用范围。
具体结论如下:
(1)标准化对降噪的影响主要体现在两个方面,一是在经验公式法选取最优主成分个数k时,缺少标准化步骤使得该方法无法正确的给出k值,从而对反演的结果造成一定的影响。二是噪声的分布不均对反演结果造成一定的影响。根据控制变量法对2011年9组晴空辐射数据做降噪处理,分析其反演结果的RMSE值,结果表明数据的标准化对反演精度的影响很小,且小于由标准化导致的k值计算误差对反演造成的影响。
(2)利用Improved PCV选取最优主成分的降噪效果与经验公式法相当。利用经验公式法对2010年和2011年两年的晴空观测数据进行计算,在进行标准化条件下k=12时IND值达到最小。在无法获取准确噪声光谱时,利用基于模拟辐射光谱确定累积方差百分比阈值的新方法,在k取27的时候模拟辐射光谱和观测辐射的偏差最小,此时利用该方法降噪反演的温度廓线的RMSE值与标准化条件下经验公式法反演结果的精度相当。因此在无法获取准确的NESR的条件下,可以使用基于模拟辐射确定PCV阈值的方法做降噪处理。
[1] Turner D D, Feltz W F, Ferrare R A. Bulletin of the American Meteorological Society,2000,81(6): 1301.
[2] Smith W L, Feltz W F, Knuteson R O, et al. Journal of Atmospheric and Oceanic Technology,1999,16(2-3): 323.
[3] Kang S, Goo T, Ou M. Journal of Atmospheric and Oceanic Technology,2013,30(7): 1433.
[4] Rodgers C D. Inverse Methods for Atmospheric Sounding: Theory and Practice. Singapore: World Scientific, 2000.
[5] Antonelli P. Journal of Geophysical Research,2004,109(D23): 102(DOI: 10.1029/2004JD004862).
[6] Huang H, Antonelli P. Journal of Applied Meteorology,2001,40(3): 365.
[7] Turner D D, Knuteson R O, Revercomb H E, et al. Journal of Atmospheric and Oceanic Technology,2006,(9): 1223.
[8] Aires F, Rossow W B, Scott N A, et al. Journal of Geophysical Research,2002, 107(D22): 4619, DOI: 10.1029/2001JD000955.
[9] Knuteson R O, Revercomb H E, Best F A, et al. Journal of Atmospheric and Oceanic Technology,2004,(12): 1777.
[10] CHEN Xiu-hong, WEI He-li(陈秀红,魏合理). Journal of Atmospheric and Environmental Optics(大气与环境光学学报), 2007, 2(2): 99.
[11] LI Jun, ZENG Qing-cun(李 俊,曾庆存). Chinese Journal of Atmospheric Sciences(大气科学),1997,21(2): 214.
[12] Turner D D, Löhnert U. Journal of Applied Meteorology and Climatology,2014,(3): 752.
(Received Feb. 10, 2016; accepted May 12, 2016)
*Corresponding author
Research on the Noise Reduction with Hyper-Resolution Infrared Spectrum Based on Improved PCV Method
HUANG Wei, GAO Tai-chang*, LIU Lei,LI Shu-lei
College of Meteorology and Oceanography, the PLA University of Science and Technology, Nanjing 211101, China
The noise reduction with observed high resolution infrared radiance is crucial to improve the accuracy and stability of the retrieval of thermodynamic profiles. When applying the principal component analysis noise filter algorithm to the observed radiance, the optimal numberkof principal components that used in the algorithm was mostly calculated with the statistical and empirical method. The percent cumulative variance method is one of the statistical methods that have been commonly used to calculatek, however, the threshold of the percent cumulative variance was determined subjectively and arbitrarily, which limits the application of this method. While the empirical method need the real-time Noise-Equivalent Spectral Radiance (NESR) to normalize non uniform noise in the observed data, but the real-time NESR needs the raw data of complex spectrum which is not easy to obtain in most cases. Aiming at the solving the problems above, a PCA noise filter based on the Improved PCV algorithm is proposed, of which the threshold is determined by iteratively calculating the difference between the simulated and reconstructed spectrum using different principal components, wherebykis determined such that the PCV is larger than the threshold. The new method solves the problem of arbitrary of the determination ofk, and at the same time it doesn’t need the real-time NESR to normalize the observed radiance. First, the impact of normalization on the noise reduction is analyzed using physical retrieval of temperature profiles; the result shows that the impact is very small, which less than the impact of calculation error ofkis caused by normalization on the retrieval of temperature profiles. Then, the noise reduction of the representative radiance data which covers four quarters of 2011 shows that, the RMSE of the retrieved temperature profile using the Improved PCV method is improved by 0.1 K compared to the factor indicator function method when the real-time NESR is not available, and it is almost the same with the latter when the normalization is done. Under the condition that the NESR is not available, the method proposed in this article could objectively and reasonably reduce the noise level of the ground-based high resolution infrared radiance.
Noise reduction of hyper-spectral; PCV method; Normalization; Newtonian nonlinear iteration retrieval technique
2016-02-10,
2016-05-12
国家自然科学基金项目(41575024)资助
黄 威,1992年生,解放军理工大学气象海洋学院硕士研究生 e-mail: huangwei_edu@sina.com *通讯联系人 e-mail: 2009gaotc@gmail.com
TP72
A
10.3964/j.issn.1000-0593(2016)11-3625-05
