非倍测度下Marcinkiewicz积分的加权Morrey估计

叶晓峰，张博涵（华东交通大学理学院，江西　南昌330013）



非倍测度下Marcinkiewicz积分的加权Morrey估计

叶晓峰，张博涵
（华东交通大学理学院，江西南昌330013）

摘要：研究了非倍测度下Marcinkiewicz积分算子M的加权Morrey估计。利用反向Ho咬lder不等式和函数分解理论，在权函数ω满足Ap（μ）条件时，获得了积分算子M是从Lp，k（ω）到弱Lp，k（ω）有界的，其中1≤p＜∞，0＜k＜1；从而将Marcinkiewicz积分算子的有界性结果推广到了非倍测度空间。

关键词：加权Morrey空间；非倍测度；Marcinkiewicz积分算子；Ap（μ）权

设μ是Rd上的Lebesgue测度，2008年Komori Y和Shirai S引入了加权Morrey空间，讨论了Hardy-Littlewood极大算子、Caldero赞n-Zygmund（C－Z）奇异积分算子和分数次积分算子等经典算子及交换子在加权Morrey空间上的有界性［1］。由于Morrey空间在方程局部正则性问题中起着重要的作用，相应的加权Morrey空间也引起了许多学者的关注，相关的结论可参考文献[2-4]。特别地，2013年傅尊伟，陆善镇和史绍光在加权Morrey空间上考虑了椭圆方程的局部正则性问题［5］。另一方面，非倍测度理论起源于Nazarov F，Treil S和Volberg A，讨论了非倍测度下的T（1）定理［6］。1998年，Darid G讨论了T（b）定理并解决了Titushkin猜想［7］(T （b）定理的证明也可参考［8］)，从而进一步引起广大学者的关注并发现在非倍测度下大部分调和分析中的经典结果仍然成立。由此引发思考，加权Morrey空间的相关结论在非倍测度下是否也仍然成立呢？

当Rd上的Radon非负测度μ满足增长性条件：对任意的方体Q奂Rd，有μ（Q）≤Cln，本文中符号C会在不同的地方出现，表示不同的常数，但都与主要参数无关；其中0＜n≤d，l是方体的边长。本文将讨论Marcinkiewicz算子在加权Morrey空间上的弱有界性问题。

设K（·，·）：Rd×Rd→R是局部可积函数，若对任意的x，y∈Rd，x≠y，存在常数C＞0，使得

以及对于任意的x，x′，y∈Rd且，存在常数0＜ε≤1和C＞0，使得。

对于上述的核函数K（x，y）以及非倍测度μ，定义Marcinkiewicz积分算子为

2005年，江寅生得到了Marcinkiewicz积分算子M是H1（μ）到L1（μ）以及L∞（μ）到RBLO（μ）有界的［9］。2007年，胡国恩，林海波和杨大春证明了积分算子M也是弱（L1（μ），L1（μ））有界的［10］。2012年，王松柏，江寅生和李德宝考虑了当权函数ω∈Aρp时，积分算子M的弱（Lp（ω），Lp（ω））有界性［11］。

非倍测度下的Muckenhoupt权Aρp，（ρ＝1）是Orobitg J和Pe赞rez C［12］首次引入的，对于一般的ρ∈［1,∞），Komori Y给出了详细介绍［13］。

定义1［13］设ρ∈［1,∞），0＜p＜∞，若对于任意的方体Q和权函数ω（x），存在正数C＞0，满足不等式

则称ω∈Aρp（μ）；若满足不等式

则称ω∈Aρ1（μ）；并令Aρ∞（μ）＝∪∞p=1Aρp（μ）。由定义可知A1p（μ）奂Aρp（μ）（简记为A1p（μ）=Ap（μ））。

定义2设1≤p＜∞，0＜k＜1，σ∈［1,∞），对于局部可积的权函数ω（x），定义加权Morrey空间为这里范数定义为

定理1设1≤p＜∞，σ，k＞1以及ω∈Ap（μ）。若Marcinkiewicz算子M是L2有界的，则M也是Lp，λ（σ，ω）到弱Lp，λ（σ，ω）有界的。即存在常数C＞0，对任意的λ＞0有方体Q奂Rd表示边长平行于坐标轴的方体，l（Q）表示其边长，ρQ便是与方体Q同心，边长是ρ倍的方体。

1 准备工作

为了定理1的证明，下面我们先介绍几个相关的引理。

引理1［12］设ρ＞1，ω∈Aρp（μ），Marcinkiewicz积分算子在L2（μ）上有界，则对于任意的1≤p＜∞，算子M也是从Lp（ω）到Lp，∞（ω）上弱有界的。即对任意的正数λ＞0和C＞0，有

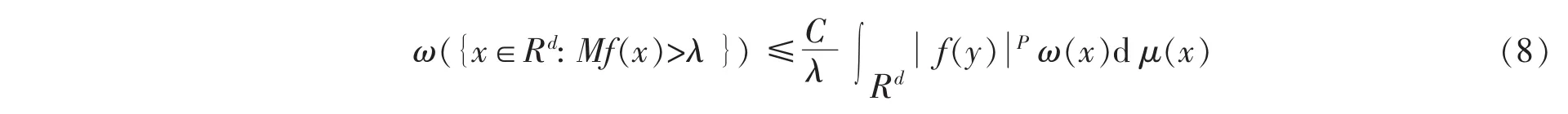
其中：f是具有紧支集的有界函数，C仅与d，ρ，p和n有关。

下面我们给出A∞（μ）的一系列等价条件。

引理2［13］对于任意的权函数ω，下列条件等价：

①ω∈A∞（μ）；

④对于任意的方体Q以及λ＞ωQ，存在正数C和β，使得

⑤ω满足反Ho咬lder不等式：即对任意的方体Q，存在正数C和δ，使得

⑥对于任意的方体Q以及子方体E奂Q，存在正数C和0＜ε＜1，使得

对于加权Morrey空间，发现参数σ＞1实际上对于空间的定义并没有本质的影响，我们有如下性质。

性质1 设1≤p＜∞，0＜k＜1以及权函数ω（x）,则对于任意的σ1σ2＞1我们有Lp，k（σ1，ω）≈Lp，k（σ2，ω）。

证明 不妨设1＜σ1≤σ2。由加权Morrey空间的定义显然有Lp，k（σ1，ω）奂Lp，k（σ2，ω），我们只需要考虑另一边的包含关系。对于任意的方体Q奂Rd，易知存在一列等边长的方体列：Q1，Q2，…，QN使得方体并且σ2Qi奂σ1Qi（i＝1，2，…，N），其中自然数运用上面的覆盖过程，对于任意的方体Q奂 Rd，我们有

因此，我们只需考虑Lp，k（2，ω）≡Lp，k（ω）的情形。

2 定理1 的证明

本节我们将利用前面所给的引理和性质来讨论定理的证明。

定理1的证明：对于任意的方体Q=Q（x0，l）以及具有紧支集的有界函数f（x）∈Lp，k（ω），我们可以将函数f分解为f = f χ2Q+ f χRd/2Q≡f1+ f2，其中χ2Q是特征函数，从而有

对于I部分，直接使用引理1，有

对于J部分，由于倍测度条件不满足，原有的方法失效。此处我们使用了权函数与测度之间的比较性质（引理2（f））以及非倍测度的增长性条件解决了问题。具体地，注意到对于任意的x∈Q,利用Minkowski不等式，有

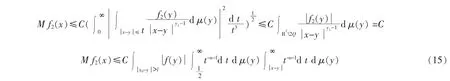
由于x∈Q，y∈Rd 2Q则有以及，从而有

另一方面，由Ap（μ）权的条件知。

并且注意到引理2.2（f），从而M f2（x）有如下估计

从而由测度μ的增长性条件μ（Q）≤Cln，则有

最后再次利用测度μ的增长性条件，从而有

从而定理得证。。

参考文献：

[1] KOMORI Y，SHIRAI S. Weighted Morrey spaces and a singular integral operator [J]. Math Nachr，2009，282（2）：219-231.

[2] WANG H. Intrinsic square functions on the weighted Morrey spaces [J]. J Math Anal Appl，2012，396（1）：302-314.

[3]王华，刘和平. Bochner-Riesz算子在加权Morrey空间上的一些估计[J].数学学报，2012，55（3）：551-560.

[4] YE X F，ZHU X S. Estimates of singular integrals and multilinear commutators in the weighted Morrey spaces[J]. J of Inequ and Appl，2012，8（1）：1－13.

[5] FU，Z W，LU，S Z，SHI S G. Boundedness of sublinear operators on weighted Morrey spaces and applications[J]. [EB/OL]. （2012－08－14）[2015-11-30]. http：//arxiv.org/pdf/1208.

[6] NAZAROV F，TREILS. VOLBERG, A. Cauchy integral and Calderón-Zygmund operators on nonhomogeneous spaces[J]. Int. Math Res Not，1997，15：703-726.

[7] David G. Unrectifiable 1-sets have vanishing analytic capacity [J]. Revista Mat Ibero，1998，14（2）：369-479.

[8] NAZAROV F，TREIL S，VOLBERG A.The Tb-theorem on nonhomogeneous spaces [J]. Acta Math，2003，190（2）：151-239.

[9] JIANG Y S. Spaces of type BLO for non-doubling measures [J]. Proc Amer Math Soc，2005，133（7）：2101-2107.

[10] HU G E，LIN H B，YANG D C. Marcinkiewicz integrals with non-doubling measures [J]. Integral Equations Operator Theory，2007，58（20）：205-238.

[11] WANG S B，JIANG Y S，LI D B. Weighted estimates for Marcinkiewicz integrals with nondoubling measures[J]. J Math Research Appli，2012，32（2）：223-234.

[12] OROGITG J，PEREZ C. weights for nondoubling measures inand application [J]. Trans Amer Math Soc，2002，354：2013-2033.

[13] KOMORI Y. Weighted estimates for operators generated by maximal functions on non-homogeneous spaces[J]. Georgian Math J，2005，12（1）：121-130.

[14] SAWANO Y，TANAKA H. Morrey spaces for non-doubling measures [J]. Acta Math Sinica，2005，21（6）：1535-1544.

（责任编辑 姜红贵）

Weighted Morrey Estimates of Marcinkiewicz Integral Operators in Non-Doubling Measures

Ye Xiaofeng，Zhang Bohan
（School of Science, East China Jiaotong University, Nanchang 330013, China）

Abstract：In non-doubling measures, the boundedness of Marcinkiewicz integral operator M is investigated on weighted Morrey spaces. When weight function ω satisfies the condition of Ap（μ）, the operators M is bounded from Lp，k（ω）to weak Lp，k（ω）, where 1≤p＜∞，0＜k＜1. It mainly generalizes the result of Marcinkiewicz integral operator in non-doubling measures.

Key words：weighted Morrey spaces; non-doubling measure; Marcinkiewicz integral；Ap（μ）

中图分类号：O174.2

文献标志码：A

文章编号：1005-0523（2016）03-0110-05

收稿日期：2015－11－30

基金项目：国家自然科学基金资助（11161021）；江西省高校科技落地项目资助（KJLD12067）；江西省青年科学基金资助（20142BAB211009）

作者简介：叶晓峰（1980—），男，副教授，研究方向为调和分析。