学为中心 分层设计 提升能力
——一节“四边形折叠”的教学设计
2016-07-12浙江省嵊州市剡城中学教育集团
☉浙江省嵊州市剡城中学教育集团 施 炯
学为中心分层设计提升能力
——一节“四边形折叠”的教学设计
☉浙江省嵊州市剡城中学教育集团施炯
在义务教育阶段取消了“实验班”“创新班”的大背景下,人的差异性又客观存在,近期我市教体局对市区初中学校优等生的培养十分重视,加强了管理和考核措施.随着初中数学思维风暴活动的深入进行,高中提前招生的方案实施,有效地促进了初中学校对优等生的管理和培养.在遵循《数学课程标准》的基础上,如何对数学知识进行变式训练和拓展提升值得我们去研究和实践,我们的平时数学教学一定要精心设计,分层落实,给优等生提供发挥才智的平台,努力克服过去优等生在课堂教学中“吃不饱”现象的存在,让他们在45分钟内发挥最大的潜能.只有在平时的教学中不断地为优等生渗透、提升相关教学内容的能力题和创新题,这样通过三年的初中教学,他们的能力水平才会有一个质的变化和提高.下面以一节“四边形折叠”的教学设计为例加以论述.
一、“四边形折叠”教学设计
1.学情分析
学生已学习浙教版八年级上册勾股定理和下册四边形的相关知识,并从七年级开始已接触到折叠问题,也初步地了解了用方程思想、数形结合思想来解决折叠问题,学生具备自主探索、合作交流、归纳总结等学习能力,但他们缺乏对折叠问题的数学本质的认识和数学思想方法的研究.
2.内容分析
“四边形折叠”问题是近年来中考的热点问题,它主要考查:一是考查动手操作和空间想象能力,二是利用轴对称考查角度和线段长度,思想方法主要是方程思想,借助勾股定理、面积和相似建立方程.在八年级开设这节课,在能力要求上比初三专题复习要低一些,重点突出折叠问题的本质,利用折叠的本质“轴对称”开启解题的思路和策略.
3.教学目标
[知识与技能目标]
理解折叠问题的本质;了解折叠问题解题策略;学会用策略解折叠问题.
[过程与方法目标]
“折”——找重叠图形、找对称轴,“叠”——还原重叠图形,关注重合线段和角,熟悉重合图形对应角、对应边相等,对称轴(折痕所在直线)是对应点连线段的垂直平分线,能通过勾股定理来构建方程解折叠问题.
[情感态度与价值观目标]
学生积极主动地参与数学活动,主动发现数学问题,主动研究和探索,主动与同学合作交流,激发学生学习数学的热情.
4.重、难点分析
重点:折叠问题的本质,重合图形、重合图形的对应边和角、对称轴的定位.
难点:应用图形的全等、重合图形的对应边和角相等、点的对称构建方程求折痕长度.
5.教学方式
教学方式:在折一折、叠一叠、剪一剪等活动中,关注数学问题的本质.数学活动之后,引导学生自主反思、归纳活动中隐含的或发现的数学规律,让学生体验和经历数学化的过程.以启发式教学为指导,启迪学生主动获取知识.
学习方式:学生自主探索、小组合作、交流、分享,充分表达自己的想法,展示解决问题的思维过程,实现“做数学—悟数学—再创造数学”的学习模式.

图1
6.教学过程
(a)问题情境.
活动1(2014年绍兴市)将一张正方形纸片,按图1所示步骤①和②,沿虚线对折两次,然后在③中沿虚线剪去一个角,展开铺平后的图形是().
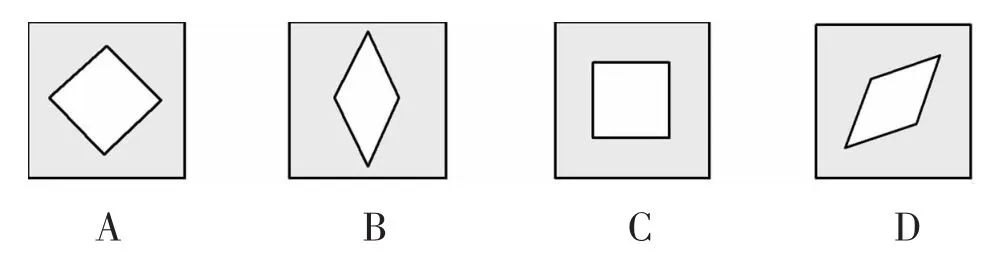
图2
教学预设:部分同学通过动手折叠得到结果;部分同学不折纸,通过还原图形得到答案;部分同学通过对选择支的排除来处理.学生进行的操作属于层次一和层次二,教师在学生操作的过程中通过设问来引导、归纳、总结上升到层次三.
层次一:动手折一折.
学生通过折一折,剪一剪,直观、形象地得到答案B.
层次二:不折纸,还原图形.
学生按照折叠的顺序,由两条折痕(对称轴)与原正方形的边垂直还原折叠的图形,得到答案B.
层次三:探索折叠的本质.
折叠的本质是:图形的轴对称变换.根据轴对称的性质可以得到以下结论.
(1)轴对称是全等变换:折叠前后重合部分图形全等,重叠图形的对应边相等,对应角相等;(2)点的轴对称性:互相重合的两点(对称点)之间的连线段必被折痕(对称轴)垂直平分(有直角三角形,可应用勾股定理得方程).
设计意图:本节课的主旨是通过对折叠问题的操作,理解折叠的本质,并应用折叠的本质属性探究解折叠问题的策略.层次一目的是通过动手操作形象、直观地解决折叠问题;层次二目的是揭示“数学更注重抽象思维”,解决折叠问题的重点是找到重合的图形及对应边、角和对称轴,并还原重合图形;层次三上升到对折叠问题本质属性的归纳总结,折叠问题的解题策略是从折叠开始,在找重合图形,确定重合的边、角和对称轴中突破.
(b)在应用中培养能力,掌握方法.
活动2如图3,折叠长方形的一边AD,点D落在BC边的点F处,已知AB=8cm,AD=10cm.
(1)说出图中哪些线段相等;
(2)写出全等三角形;
(3)求出EC的长.

图3
教学预设:学生独立完成,并请一位同学上讲台讲题.在学生讲题的过程中归纳出解题的本质:(1)折叠前后重合的线段长度相等;(2)折叠前后重合的两个三角形全等;(3)在直角三角形中,利用勾股定理,列出方程求解问题.如图3,重合的图形有:△ADE≌△AFE,重合的线段有:AF=AD=10,EF=ED,若设EC=x,则由Rt△EFC得到方程42+x2=(8-x)2.
设计意图:本活动主要考查轴对称是全等变换:折叠前后重合部分图形全等,重叠图形的对应边相等;并把条件集中到一直角三角形中根据勾股定理得到方程,求出未知数,让学生从中感悟折叠问题中的数学思想和解题方法.
变式1:如图4,折叠长方形的一边AD,使D点与B点重合.
(1)求证:BE=BF;
(2)若AB=8cm,AD=10cm,求折痕EF的长.
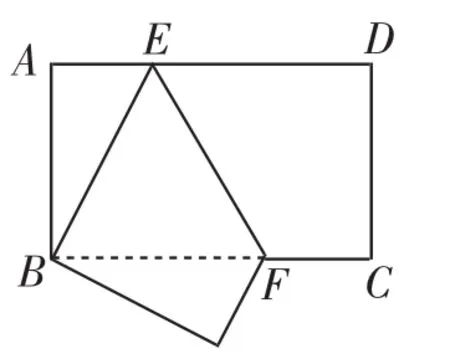
图4
教学预设:学生在解本题时会有困难,因为他们对“折痕”所蕴含的数学本质没有理解,“折痕EF”:(1)是对称线段所夹角(∠BED)的平分线;(2)是对称点连线段BD的垂直平分线.所以教师要求学生从折纸的过程中,画出折痕EF和线段BE,再还原后,连接BD,让学生自己来感悟“折痕”所蕴含的数学知识,以此来突破本题.
希望学生通过合作、小组交流呈现另外的解法:(1)由折痕知∠BEF=∠DEF,再由平行线得∠DEF= ∠BFE;(2)一是先证四边形EBFD为菱形,利用面积求折痕EF的长度,二是作EG⊥BC于G,通过Rt△EGF求折痕EF的长度.
设计意图:本活动的目的是通过(1)的证明,让学生感悟在同一题目中如果有平行线和角平分的条件,那么就能推得等腰三角形,这一特征在解题中非常重要.通过(2)的解答,利用点的对称性解折叠问题.通过现场折纸、画图揭示折痕EF是线段BD的垂直平分线,自然过渡辅助线BD;同时很好地应用了折叠问题的解题策略:(1)折纸;(2)还原重叠图形.
变式2:(2013年嵊州市八年级数学竞赛题)如图5,点M是正方形ABCD的边AB的中点,连接DM,将△ADM沿DM翻折得到△FDM,延长MF交DC的延长线于点E,求CE∶DE的值.
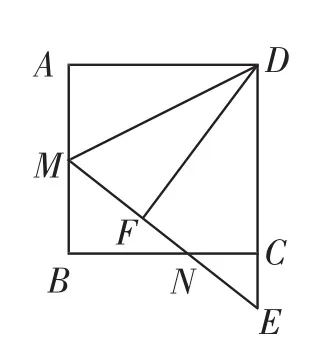
图5
教学预设:学生在解本题时会有困难,因为他们对“折痕”所蕴含的数学本质没有理解,“折痕DM”:(1)是对称线段所夹角(∠AMF)的平分线;(2)在已有角平分线和平行线的条件下不能找出等腰三角形.所以教师启发学生在变式1的基础上,找出等腰三角形,得出相等线段.折痕DM是∠AMF的平分线,再通过AB∥CD,得出∠AMD=∠FMD=∠MDE,得到DE=ME.让学生自己来感悟“折痕”所蕴含的数学知识,以此来突破本题的难点.
设计意图:本变式的目的是在变式1的基础上,进一步提升解题能力,加强几何直观,掌握基本图形的性质,感悟数学思想方法.(1)基本图形:在平行线、角平分、等腰三角形三个条件中,只要有两个成立,就能推得第三个成立.(2)感悟方法:在折叠问题中,通常通过等量线段的转换,使已知条件集中到同一个直角三角形中,再利用勾股定理,列出方程求解问题.
(c)在挑战中提升能力,感悟思想.
活动3如图6,将正方形ABCD 沿AD、BC的中点M、N对折,得到折痕MN.再将点C折至点P的位置,折痕为BQ,连接PQ、BP.
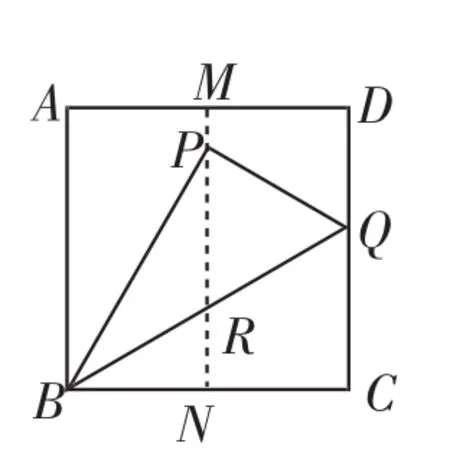
图6
回答下列问题,并说明理由.
问题1:找出图中相等的线段.
问题2:找出成两倍数量关系的线段.
问题3:探求∠PBC的度数.
迎接挑战,你对本题还能提出什么问题?看哪个小组提出的问题多.
教学预设:活动目的是通过找问题的隐含条件“BP=BC=2BN”来“探求∠PBC的度数”.然后通过学生小组合作自己提出问题并解决问题把课堂推向高潮.
教师为防学生提不出问题,可以引导学生从图形的形状、角度、线段长度关系上提出问题.
最后教师留给学生一道课后探索题:“如何用一张正方形的纸片折出与正方形边长相等的正三角形.”
设计意图:正方形的特殊性,尽管题中没有出现线段长度,但是在折叠过程中隐含着线段间的数量关系,通过揭示隐含的数量关系解折叠问题来提升学生的能力;并利用课后探索题来提高学生对学习数学的兴趣、热情、能力.
(d)知识梳理和作业布置.
一个问题:四边形折叠问题.
两种策略:动手“折”——定重叠图形、对称轴;还原“叠”——定重合的线段和角.
三个关注:图形的全等,点的对称,方程思想.
作业:学案上的必做题和选做题(略).
二、教学反思
本节课是围绕“四边形折叠”设计的系列活动,有利于学生针对问题情境,借助所学知识,或独立思考,或与他人合作,经历提出问题、分析问题和解决问题的全过程.
本节课着力体现了学为中心,分层教学的主题,教学过程分为三个层次.
第一层次是“做数学”的过程,使学生初步体会折叠问题所蕴含的数学知识和数学原理.
活动1,学生在折叠纸片、还原图形中“做数学”.
第二层次是“悟数学”的过程,从做数学中悟出折叠的本质和解折叠问题的策略.
活动2,学生在折叠图形中,利用对称性,获得相关图形的性质,感悟数学思想方法.
在本堂课教学中,通过变式训练和能力提升,使学生对数学知识、数学问题、数学思想有了更深入的理解和感悟.让学生自己经历数学学习的过程,真切地体会、充分地品尝了探究、解决问题过程的乐趣,更深地领略了数学过程的内在美、简洁美和统一美,既培养了多种能力又陶冶了情操,效果完美、有意义.
第三层次是“再创造数学”的过程.
在活动3中,学生提出问题并自己解决问题;问题“如何用一张正方形的纸片折出与正方形边长相等的正三角形”实现了数学的再创造.
本课的设计既考虑到学生已有的知识经验,也考虑到问题的数学实质;整节课的活动给学生提供了展示、讲解、质疑的平台,教师只起点拨、引导的作用;在学生解决问题的过程中,教师既提出了启发学生思维的问题,也注意到在教学过程中帮助学生总结、归纳、升化知识和培养学习能力.Z

