炮兵对有生力量压制比的仿真计算方法
2016-07-12吕学志常利胜
吕学志,常利胜
(总参炮兵训练基地模拟训练中心,河北 宣化 075100)
炮兵对有生力量压制比的仿真计算方法
吕学志,常利胜
(总参炮兵训练基地模拟训练中心,河北宣化075100)
摘要:为了评估炮兵对有生力量压制效果,应用离散事件仿真方法建立了炮兵射击有生力量仿真模型,提出一种炮兵对有生力量压制比的仿真计算方法。首先,给出了压制比的概念与模型。然后,建立了基于离散事件仿真的炮兵射击有生力量模型。最后,结合实例验证了仿真计算方法的正确性。
关键词:有生力量,压制比,离散事件仿真,炮兵,射击效率评定
0 引言
国内许多研究人员开始对炮兵对有生力量射击效率进行研究,如文献[1-5],但存在一些不足,一是对炮兵压制效果研究不够,大多数研究人员只研究杀伤效果,而忽略了炮兵的压制效果,至今还没有一种压制比的度量与计算方法。二是假设有生力量在遭到炮火射击时一直保持一种姿势,不会采取减少毁伤的应对措施,这与战场实际情况非常不符,无形中会影响炮兵射击效果的准确度。所以本文给出有生力量压制比的度量模型,提出基于离散事件仿真的炮兵对有生力量压制比的仿真计算方法,并在仿真模型中考虑了有生力量采用不同姿势来减少受到的损伤,使模型更加贴合战场实际情况,并且为评估炮兵射击效率提供新方向和思路,为炮兵火力运用提供指导。
1 射击效率评定与毁伤效果
1.1射击效率评定
炮兵主要以火力完成作战任务,而火力要靠射击来达成。对炮兵射击的基本要求是:以最少的弹药,适时地对目标达到最佳的射击结果。射击效率就是对上述基本要求所达到的程度。由于炮兵射击要受到许多客观因素的影响,因此,射击结果是一种随机现象,就需要以平均射击结果来衡量某种武器系统或某种射击方法在一定条件下的射击效率。除个别情况外,通常不能在战场上直接评定射击效率,而往往需要采用模拟的方法进行评定。模拟方法可分为物理模拟和数学模拟两类:实验法属于物理模拟,解析法和统计试验法属于数学模拟[2]。
1.2毁伤效果
毁伤是指炮弹效力对目标毁伤和杀伤的作用结果。对有生力量来说,毁伤可能指使其死亡、受伤、压制,这几种效果都会使有生力量失去战斗力,或者暂时失去战斗力。有生力量的毁伤效果与弹着点距离r有密切关系,通常表示为弹着点距离r的函数。
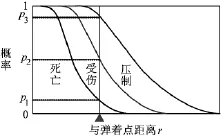
图1 毁伤效果曲线
2 压制比计算原理
火力压制是以强于对方的火力毁伤敌兵力兵器,并限制其行动的作战行动。目的是削弱或暂时剥夺敌还击能力。炮兵火力使友邻步兵部队在不受敌方火力妨碍、观察的情况下向敌机动。指挥官唯一明确的评估方式是敌方是否受到压制,敌方是否向友邻步兵射击。所以,必须防止敌方步兵部队向友邻步兵射击。显然,受到杀伤或压制的敌人不能向友邻部队射击。然而,受伤的敌人仍然很危险。该指标中“压制”这一术语用来指杀伤与压制的综合效果。
我们关注的是,某一时间段目标区域敌人受到压制的平均比。时间段T取决于步兵机动同时炮兵射击持续时间。令Kt表示时间t敌方伤亡人数,令St表示时间t敌方受到压制人数。对于一次射击任务,T时间段敌方有生力量压制比是
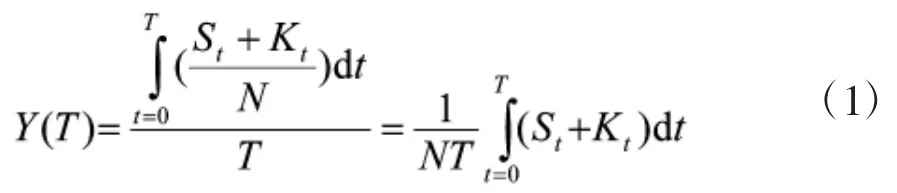
其中,N是目标区域敌人总人数。
由于炮兵射击具有随机性,一次射击任务中敌方有生力量压制比只是一个样本,不能反映全部射击任务的压制比特征。由于压制比公式比较复杂,射击任务中,由于射击的随机性,压制人数与伤亡人数不断变化,解析的方法是无法得到压制比的,只能使用仿真的方法。在仿真中式(1)转化为以下公式:

其中,Tsi是目标i在射击任务中总的压制时间。
压制比FS是射击任务期间敌方受压制人数的平均比。

其中,n是仿真中火力任务重复的次数。
3 炮兵对有生力量射击仿真模型
3.1模型假设
仿真模型假设射击单位是炮兵连(6门火炮),每门火炮向目标发射有限数量的相同炮弹。炮兵射击目标是随机分布于一定区域中的暴露有生力量,敌方人员最初处于站立姿态,受到压制之后采取蹲伏姿态,再次受到压制或者受伤之后采取匍匐姿态,受到压制的人员经过一定时间不受压制,恢复站立姿势。具体人员状态转换如图2所示。

图2 人员状态转换图
3.2弹着点的模拟
6门炮分别对不同瞄准点进行射击,射击误差主要分为平均弹着点误差与散布误差。平均弹着点误差主要是由于气象误差、目标位置误差、测地误差、弹道准备误差、技术准备误差以及其他误差组成。散布误差是火炮、弹药、操作和气象等几方面因素的微小差异影响的综合结果。平均弹着点误差与散布误差都服从二维正态分布。所以第i门火炮发射炮弹的弹着点坐标(xi,yi)可由以下公式计算。

其中,(x0 i,y0i)是第i门火炮的瞄准点坐标,δD与δR分别是平均弹着点误差的射程标准偏差与方向标准偏差,σD与σR分别是散布误差的射程标准偏差与方向标准偏差,w1与w2分别是正交、相互独立的标准正态分布随机数,同样,w3与w4也分别是正交、相互独立的标准正态分布随机数[6]。
3.3毁伤概率函数
毁伤概率函数是弹着点与目标距离(这一距离被称为误差距离r)的函数。有生力量杀伤概率函数D(r)如下:

有生力量压制概率函数如下(该函数由美国陆军战斗开发试验司令部提出):

其中,参数A≥0与B≤0。

图3 事件调度法程序结构
3.4建立仿真模型
本文采用事件调度法进行程序设计,程序结构如图3[7]。仿真程序中非常重要的数据结构是事件表、目标的坐标与状态。目标的数据包括坐标位置、状态、压制(伤亡)开始,压制累计时间。事件表相当于事件构成的队列,事件表中事件的属性包括时间、事件类型(包括发射事件、弹着事件与压制结束事件)、火炮编号(发射事件、弹着事件)或者人员编号(压制结束事件)。弹着事件、压制结束事件与发射事件对应的流程图分别为图4~图6所示。
每次仿真的持续时间是从火炮首次射击开始到受到压制的所有人员最终恢复正常状态的这段时间。仿真结束条件是事件表中没有任何事件。
3.5仿真数据

图4 弹着事件的流程图

图5 压制结束事件的流程图
输入数据。仿真的输入数据包括火炮门数(6门)、火炮平均弹着点误差(δD=79.5与δR=33.1)、散布误差(σD=47.4与σR=5.3)、火炮射程(16 km)、炮弹飞行时间(60 s)、每门炮弹发射间隔时间(服从均值为25 s,标准偏差为5 s的正态分布)、目标为暴露有生力量(分布400 m×400 m区域的150个敌方人员)、人员压制持续时间(服从均值为30 s,标准偏差为5 s的正态分布)、杀伤概率函数与压制概率函数参数(如表1所示)。目标区域如图5所示,其中红“*”表示敌方人员,“×”表示目标中心,“矩形”表示火炮的瞄准点,矩形上的数字表示火炮的编号。

图6 发射事件的流程图
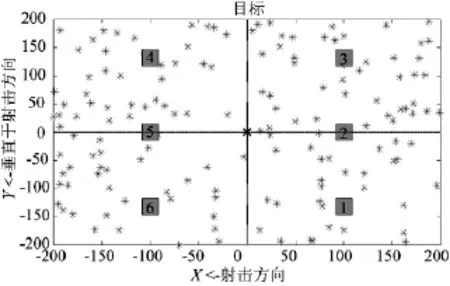
图7 目标区域

表1 杀伤概率函数与压制概率函数参数表
输出数据。使用Matlab编写仿真程序。运行一次仿真程序,得到一次射击压制比累积分布。如图6所示。将发射炮弹总数分别设定为12、24、36、48,分别运行仿真模型1 000次,得到不同炮弹总数情况下的压制比,如表2所示。
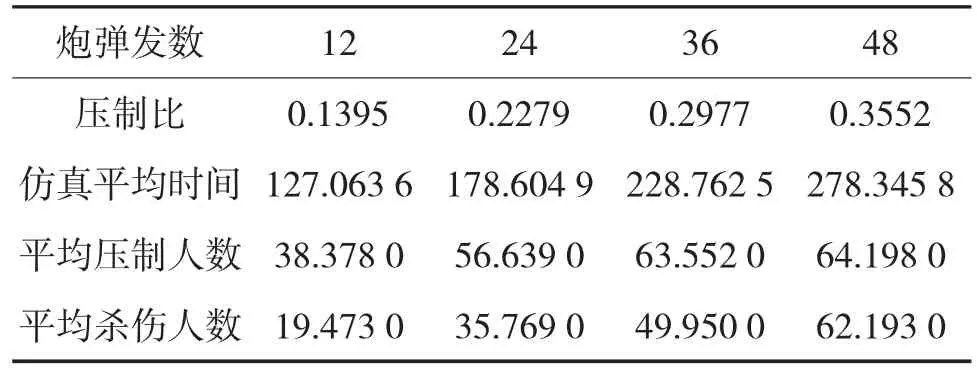
表2 仿真统计结果
3.6仿真结果分析

图8 一次射击毁伤累积分布(12发)

图9 一次射击毁伤累积分布(24发)
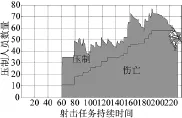
图10 一次射击毁伤累积分布(36发)

图11 一次射击毁伤累积分布(48发)
本文中,进行4次仿真实验,每次实验中炮弹发射总数分别为12、24、36、48,仿真1 000次,并对仿真结果进行了简单的数理统计,见表2。从表中可以看出随着炮弹发射总数增加,压制比也随之增加,但是增加的幅度逐渐减弱;随着炮弹发射总数增加,仿真时间也等比例增加;随着炮弹发射总数增加,平均压制人数与平均伤亡人数都不断增加,但是增加幅度都不断减弱。比较图8~图11,发现随着炮弹总数增加,毁伤效果不断加大,但是同一时刻仅受到压制的人员比例不断减少。
4 结论
本文给出有生力量压制比的度量模型,提出基于离散事件仿真的炮兵对有生力量压制比的仿真计算方法,并在仿真模型中考虑了有生力量采用不同姿势来减少受到的毁伤,使模型更加贴合战场实际情况,并且为评估炮兵对有生力量射击效率提供新方向和思路,为炮兵火力运用提供指导。
参考文献:
[1]程云门.评定射击效率原理[M].北京:解放军出版社,1986.
[2]张平乐,柳建民,刘冰,等.炮兵射击效率评定(试用)[M].宣化:炮兵指挥学院,2006.
[3]赵新生,刘玉文,许梅生,等.新弹种弹道与射击效率评定[M].北京:兵器工业出版社,2004.
[4]钟宜兴,刘怡昕.炮兵射击学[M].南京:炮兵学院南京分院,2004.
[5]江华,许梅生,邱超凡,等.炮兵射击基本理论分析[M].北京:兵器工业出版社,2004.
[6]路航,石全,胡起伟,等.炮兵营射击的弹着点模拟及射击误差分析[J].指挥控制与仿真,2011,33(03):110-112.
[7]肖田元,范文慧.系统仿真导论[M].第2版.北京:清华大学出版社,2006.
Simulation Method for Suppression Ratio of Artillery Firing to Living Personnel
Lü Xue-zhi,CHANG Li-sheng
(Artillery Training Base of General Staff,Xuanhua 075100,China)
Abstract:In order to evaluate suppression effect of living personnel,it established simulation model of artillery firing to living personnel with discrete event simulation approach,and it put forward simulation methods of living personnel suppression ratio. Firstly,it puts forth concept and model of suppression ratio. Then,it establishes simulation model of artillery firing to living personnel based on discrete event simulation. At end,it validates simulation methods with an example.
Key words:living personnel,suppression ratio,discrete event simulation,artillery,fire efficiency evaluation
中图分类号:E92;TJ306+.3
文献标识码:A
文章编号:1002-0640(2016)05-0093-04
收稿日期:2015-03-15修回日期:2015-05-20
作者简介:吕学志(1979-),男,汉,河北宣化人,讲师,研究方向:维修工程。
