基于估计协方差MME检测的频谱感知算法
2016-07-12姚少林张政保刘广凯
姚少林,张政保,许 鑫,刘广凯
(军械工程学院,石家庄 050003)
基于估计协方差MME检测的频谱感知算法
姚少林,张政保,许鑫,刘广凯
(军械工程学院,石家庄050003)
摘要:针对小采样数据长度下,采样协方差矩阵对统计协方差矩阵估计不准,影响传统最大最小特征值(MME)检测算法检测性能的问题,提出一种基于逼近收缩(OAS)矩阵估计的改进MME检测算法。首先利用OAS估计量对采样数据做协方差矩阵估计,再对估计协方差矩阵特征值分解,将最大最小特征值之比作为检测统计量,克服了传统MME算法检测门限随采样点大幅波动的缺陷,提高了检测门限的鲁棒性。仿真结果表明,所提算法的检测门限具有鲁棒性,检测性能提高了1 dB~2 dB。
关键词:认知无线电,频谱感知,最大最小特征值,协方差矩阵估计,随机矩阵理论
0 引言
频谱感知是实现认知无线电(Cognitive Radio,CR)技术的关键环节。次级用户(Secondary User,SU)对空闲频段和主用户(Primary User,PU)信号的准确感知是实现频谱高效利用的前提[1-2]。
近年来,利用接收信号采样协方差矩阵的频谱感知方法发展迅速。有学者先后提出协方差绝对值(Covariance Absolute Value,CAV)、最大最小特征值(MME)、能量最小特征值(Energy-Minimum Eigenvalue,EME)、最大最小特征值之差(Difference Between the Maximum and the Minimum Eigenvalue,DMM)的检测算法[3-6]。这些算法以高维度随机矩阵理论(Random Matrix Theory,RMT)为基础,利用了采样数据长度趋于无穷时,Wishart随机矩阵最小特征值的渐进极值定理和最大特征值服从Tracy-Widom分布定理,充分利用采样协方差矩阵的元素和特征值分布的差异构造检测统计量,在存在噪声功率不确定性时,这些算法较ED有更好的检测性能。然而,这些算法都利用了采样数据长度无穷的假设条件,当采样数据长度较小时,利用采样协方差矩阵替代统计协方差不够准确,因此,对小采样数据下的统计协方差矩阵进行有效估计是提高检测性能的基础。
统计协方差矩阵的估计是信号处理领域的一个基本问题[7-8]。采样数据长度趋于无穷时,采样协方差矩阵估计量是统计协方差矩阵的最大似然估计且是无偏估计,但在采样数据长度较小、数据维度较高时,采样协方差矩阵估计量不满足最小均方误差(Minimum Mean-Squared Error,MMSE)的要求,是统计协方差矩阵的一种比较差的估计量[7-8]。Stein证明了对采样协方差矩阵收缩估计的方法可以获得对统计协方差矩阵更好的估计性能[9]。Ledoit和Wolf提出了LW(Ledoit-Wolf)估计量[10-11]。此后,有学者提出了RBLW(Rao-Blackwell Ledoit-Wolf)和逼近收缩(Oracle Approximating Shrinkage,OAS)改进的估计量,并将其应用于波束成形和无线传感器网络信号检测,发现OAS方法有更好的估计性能[8]。
根据以上分析,本文提出基于OAS方法的估计协方差矩阵MME检测算法。算法利用OAS方法得到估计的协方差矩阵,将估计协方差矩阵的MME之比作为检测统计量。仿真结果表明,在采样数据长度较小的情况下,所提算法的检测门限具有稳定性,同时较MME检测算法有更好的检测性能。
1 系统模型
在认知无线电网络(Cognitive Radio Network,CRN)中,假设SU仅有一个接收天线,基于单个SU的观测对PU信号进行频谱检测。令x(t)为经过未知信道的时间连续的接收信号,Ts为采样周期,则接收的采样可以表示为

认知用户对某频段信号的检测实际上属于二元假设检验问题,检测模型如下:
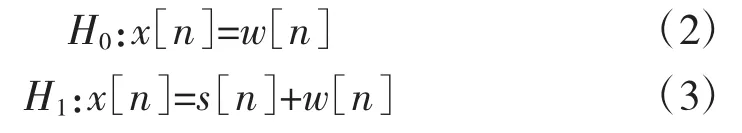
H0表示接收信号仅含噪声,PU信号不存在,该频段空闲。H1表示接收信号包含PU信号和噪声信号,该频段被占用。其中,假设w[n]是均值为0、方差为的加性高斯白噪声,w[n]的每次采样独立同分布(i.i.d)。s(n)是经过未知信道且信号分布未知的PU信号采样,且噪声和PU信号不相关。
假设在第i个感知周期内的采样数据用矩阵Γx,i表示,Γx,i中列向量的元素为L个连续采样数据(也被称为平滑因子),可以用列向量xi来表示,Γx,i中行向量的元素为N个连续采样数据[12]。采样数据构造的感知矩阵结构如下
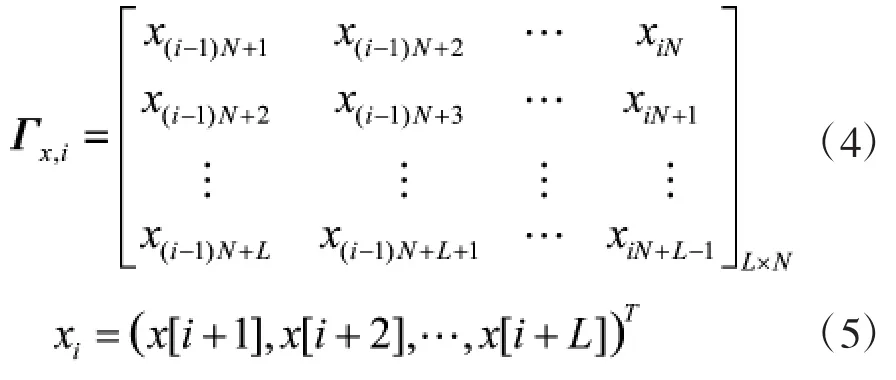
其中,xi~N(,Rx),为均值,Rx为统计协方差矩阵。每个感知周期共包括Ntot个采样数据,根据感知矩阵的结构可得到下式

实际上,观测信号的协方差矩阵是未知的。采样协方差矩阵是统计协方差矩阵Rx的一种经典估计量。假设采样信号的均值为0,则采样协方差矩阵可以表示为
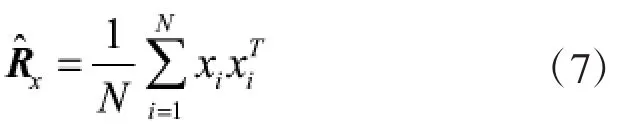
2 基于估计协方差矩阵的MME检测算法
频谱感知作为CR的基础,要求必须能够在保证虚警概率(Pfa)的前提下,最快地检测出某频段是否被占用。提高采样数据长度,固然能够提高检测概率(Pd),同时也会增加感知时间,增加认知设备的计算量,因此,小采样数据长度条件下的频谱感知尤为重要。小采样数据长度会带来统计协方差矩阵估计不准确的问题,同时基于高维度RMT的最大特征值分布定理和最小特征值的极值定理不再适用。
2.1统计协方差矩阵估计
OAS估计量利用非随机系数使其对统计协方差矩阵估计的均方误差最小[8],是以下方程的解。
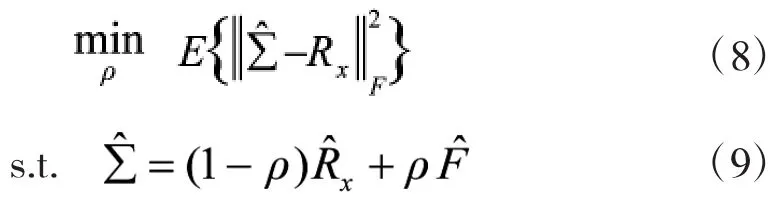

其中I为L维单位阵,Tr(·)为迹运算。
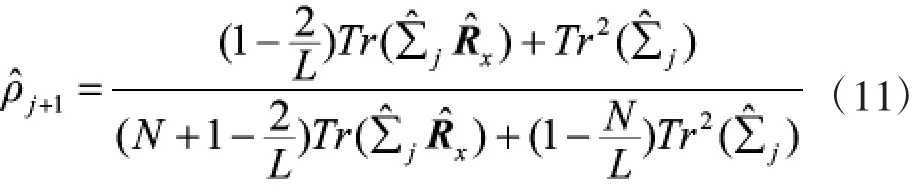
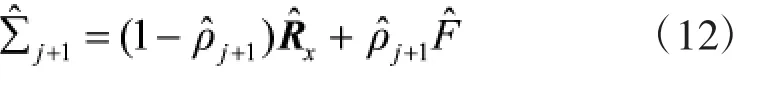
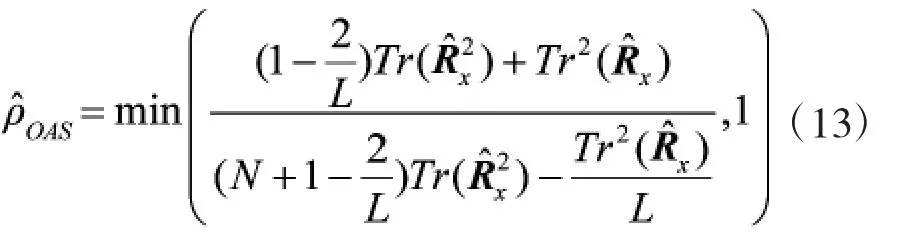
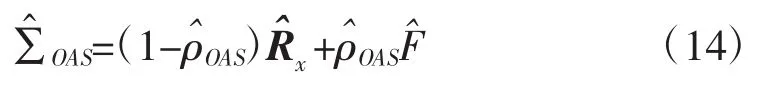
采用OAS矩阵估计的方法对统计协方差矩阵进行估计实际上是对采样协方差矩阵作了预测,当信号为纯噪声信号时,估计协方差矩阵就会收缩至目标矩阵,当PU信号存在时,估计协方差矩阵就会逼近采样协方差矩阵。因此,估计协方差矩阵的特征值结构必然与采样协方差矩阵的特征值结构不同。
2.2MME算法
RMT应用于频谱感知以来,根据Wishart矩阵特征值极值分布定理和特征值极值定理[13-14],利用采样协方差矩阵最大特征值和最小特征值极值的渐进性质出现了很多算法[15-19]。令Rx的特征值按照顺寻排列为λ1≥λ2≥…≥λL。如果PU信号不存在,从理论上讲λ1=λ2=…=λL=σ2n,此时λ1/λL=1。PU信号存在时,λ1>λL,此时λ1/λL=1。因此,可以将最大最小特征值的之比λ1>λL作为检测统计量,判断PU信号有无。最大特征值λ1和最小特征值λL由估计协方差矩阵OAS特征值分解得到。
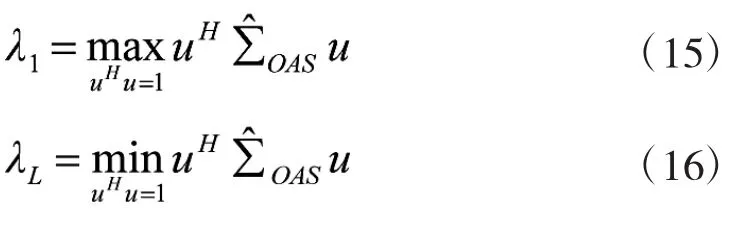
检测统计量为

MME检测算法将接收数据采样协方差矩阵的MME之比作为检测统计量,如果采样数据长度较小,其检测性能也会相应降低。在高维度小采样长度情况下,OAS比x对Rx的估计更加精确,因此,利用OAS替代x计算特征值极值得到的检测算法会更加精确。
2.3改进MME算法的计算步骤
根据以上分析,本文提出基于OAS方法的估计协方差矩阵MME检测算法,并与传统MME检测算法做对比。算法的具体计算步骤如下:
步骤1:通过计算机仿真确定相应实验条件下的检测门限γ。
步骤2:设定感知矩阵的采样数据长度N,确定感知矩阵Γx,i。
步骤3:检测过程。
根据式(10)~式(13)计算OAS矩阵估计方法的收缩系数OAS和矩阵。
根据式(17)计算出最大最小特征值之比TN。步骤4:判断过程。
如果TN>γ,PU存在。否则,PU不存在。
3 理论分析和检测门限
3.1RMT的特征值分布定理
在H0假设条件下,x(n)不存在PU信号,则x(n)服从均值为0,方差为IL的L维高斯分布。则噪声的采样协方差矩阵Rn(Ns)服从L维Wishart分布[13],即
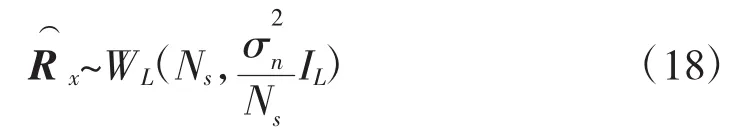
其中,WL(·,·)表示L维Wishart分布。
Wishart随机矩阵特征值的联合概率密度函数表达式非常复杂。最近,I.M.Johnstone和K.Johansson对Wishart随机矩阵的最大特征值分布进行了研究[13],其成果如下
定理1:若噪声为实噪声,令A(N)s=(Ns/σ2n)·Rn(N)s,μ=2,υ=(1/3,假设=ρ(0<ρ<1),则依概率收敛于Tracy-Widom第1分布。其中,R(nN)s为H0条件下采样协方差矩阵,λmin(A(Ns))为矩阵A(Ns)的最大特征值。
白志东等人对Wishart矩阵的最小特征值极限值的研究成果如下[14]
基于以上定理,λmin、λmax分别为矩阵(A(Ns)的最大最小特征值,最大最小特征值可近似表示为
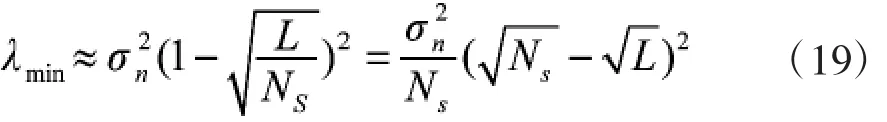
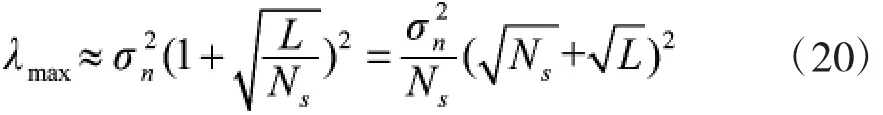
3.2检测门限的确定
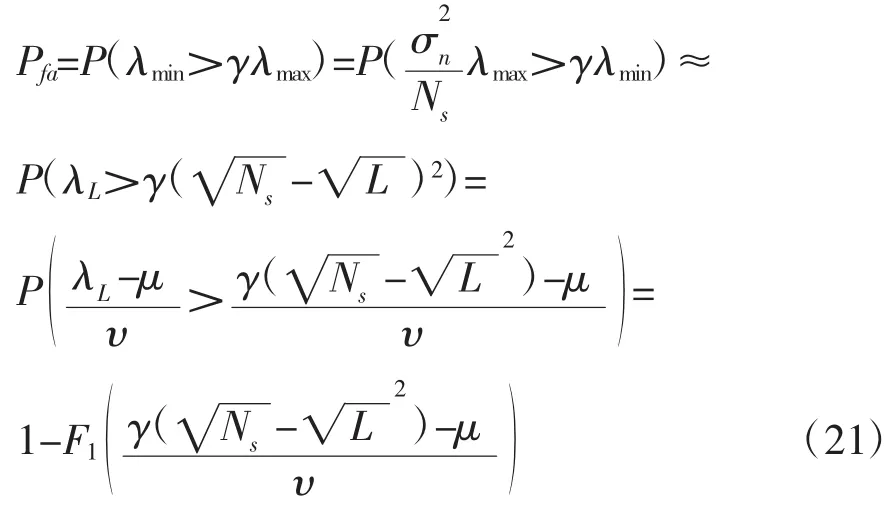
由上式可以推导出MME检测算法的理论门限值[4]为
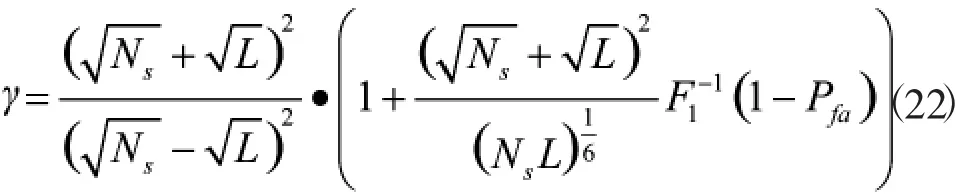
式(22)是传统MME检测的理论门限的封闭表达式,用于和本文所提改进算法作对比。理论门限的推导需要知道在无PU信号时检测量取值分布的封闭表达式,通常难以实现。实际频谱感知过程检测门限可以通过计算机仿真确定,随机信号的检测门限是时变的,满足虚警为0.1时,多次实验得到检测门限也会在一定范围波动,因此,本文将多次独立实验得到的检测门限值的μ+σ之和作为判决门限,可以满足每次实验虚警都小于0.1的需要。
4 仿真分析
为了验证所提算法性能,利用Matlab仿真的方法,对高斯白噪声条件下QPSK信号进行检测。本文采用蒙特卡罗仿真的方法来比较两种算法的检测性能。为了便于分析,QPSK信号基带码元速率为2 kb/s,载波信号为10 kHz,数据采样速率为50 kHz,满足奈奎斯特抽样定理要求。
4.1检测门限数值仿真
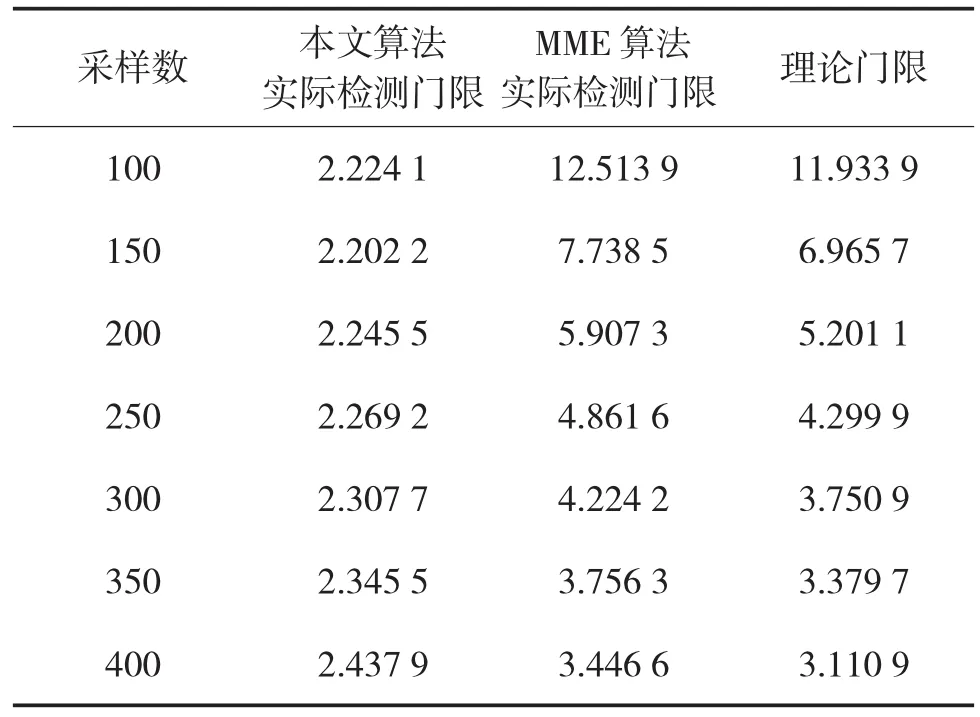
表1 不同采样数下两种算法实际门限和理论门限对比
表1是不同采样数下的两种算法的实际门限和根据式(22)得到的理论门限的对比表。在L=30条件下,分别采用两种算法对AWGN信号进行MME检测,进行1 000次独立检测,并计算每次实验的TN值,假定Pfa=0.1,得出相应的门限值。检测统计量TN是随机变量,做10次独立仿真实验,可以得到10个不同的检测门限值,计算TN的均值μ、均方根σ,并把μ+σ之和作为实际门限值。采样数据长度按照每次增加50个的步长变化时,本文所提算法的实际检测门限值缓慢增大,但数值相对稳定,且与理论值相差较大。传统MME检测算法的实际检测门限与理论检测门限变化趋势相同,且数值稍大于理论值,因此传统MME检测算法利用理论值计算门限有一定的合理性,而本文所提算法采用式(22)计算检测门限是不可行的。可以得出如下结论,估计协方差矩阵改变了采样协方差矩阵的特征值结构,在采样数不同时,两种假设条件下检测统计量的概率密度函数波动性减小,门限值趋于稳定,而传统MME检测算法的门限值,随采样数变化波动巨大,对采样数变化敏感。在采样数据长度较小时,所提算法的检测门限具有鲁棒性。
表1对门限变化趋势作了分析,确定门限值只进行了10次实验,要精确仿真出不同采样数据长度下的具体门限值,需要对检测门限作更多次数的仿真。图1是采样数据长度不同时,本文算法检测门限的变化情况,并对前20次仿真结果进行了局部放缩。作50次独立仿真实验确定门限值,在N=100时,随机变量TN的均值μ为2.152 5,方差σ2为0.005 0,N=200时,均值μ为2.184 8,方差σ2为0.002 4。本文将μ+σ值大小作为判决门限。因此,本文所提算法,在N=100时,检测门限为2.222 5,N=200时,检测门限为2.233 8。本文采用固定检测门限的方法对PU信号进行频谱检测。
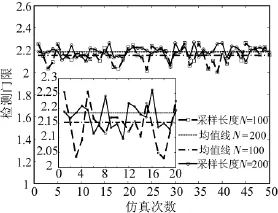
图1 不同采样长度时的检测门限
4.2检测性能分析
频谱感知算法的检测性能通常根据满足Pfa要求时Pd的大小来衡量。为了保证PU通信不受干扰,一般将Pfa设置为0.1。
图2是采样长度不同时检测概率和虚警概率随信噪比变化的曲线变化。图2(a)中,N=100时,本文所提算法的检测概率明显优于MME检测算法,在Pd达到0.9时,Pfa全部低于0.1,性能相差大约2 dB。图2(b)中,N=200时,本文所提算法明显优于MME检测算法,Pd达到0.9时,Pfa绝大多数低于0.1,性能相差大约1 dB。可以看出,本文所提算法在采样数较小的情况下较MME算法检测性能明显提高。同时说明,采用μ+σ作为检测门限可以保证虚警概率在0.1之下,并具有很好的稳定性。

(a)N=100 (b)N=200图2检测概率和虚警概率随信噪比变化的曲线比较
5 结论
以传统MME检测算法为基础,提出一种基于OAS方法的估计协方差矩阵MME检测算法。算法利用OAS方法对高维度小采样数下的统计协方差矩阵进行估计,减小了估计误差,提高了协方差矩阵估计精度,通过对估计的协方差矩阵特征值分解得到最大最小特征值。估计协方差矩阵改变了采样协方差的特征值结构,因此,采用计算机仿真实验确定检测门限。仿真结果表明,在采样数据较少时,与传统MME检测算法相比,本文算法的检测门限具有鲁棒性,检测性能提高了1 dB~2 dB。该算法适用于低信噪比、小采样数据条件下的频谱检测。本文没有给出所提算法检测统计量的概率分布,不能给出检测门限和检测概率的封闭表达式,这可以作为下一步研究的重点。
参考文献:
[1]ZENG Y,LIANGY C,HOANG A T,et al. A review on spectrum sensing for cognitive radio:challenges and solutions[J]. EURASIP Journal on Advances in Signal Processing,2010 (2):18-21.
[2]WANG B,LIU K J R. Advances in cognitive radio networks:A survey[J]. Selected Topics in Signal Processing,IEEE Journal of,2011,5(1):5-23.
[3]ZENGY,LIANGYC.Spectrum-sensingalgorithmsfor cognitive radio based on statistical covariances[J]. Vehicular Technology,IEEETransactionson,2009,58(4):1804-1815.
[4]ZENG Y,LIANG Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. Communications,IEEE Transactions on,2009,57(6):1784 - 1793.
[5]王颖喜,卢光跃.基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报,2010,42(11):2571-2575.
[6]卢光跃,弥寅,包志强.特征值极限分布的改进合作频谱感知[J].信号处理,2014,40(3):261-267.
[7]CHEN Y,WIESEL A,ELDAR Y C,et al. Shrinkage Algo-rithms for MMSE Covariance Estimation[J]. Signal Processing,IEEE Transactions on,2010,58(10):5016 - 5029.
[8]CHEN Y,WIESEL A,HERO A O. Robust shrinkage estimation of high-dimensional covariance matrices[J]. Signal Processing,IEEE Transactions on,2011,59(9):4097-4107.
[9]STEIN C. Estimation of a covariance matrix In Rietz Lecture [C]// 39th Annual Meeting,IMS,Atlanta,GA,1975.
[10]LEDOIT O,WOLF M. A well-conditioned estimator for large-dimensional covariance matrices[J]. Journal of multivariate analysis,2004,88(2):365-411.
[11]LEDOIT O,Péché S. Eigenvectors of some large sample covariance matrix ensembles[J]. Probability Theory and Related Fields,2011,151(1-2):233-264.
[12]LIN F,QIU R C,BROWNING J P. Spectrum Sensing with Small-Sized Datasets in Cognitive Radio:Algorithms and Analysis[J]. arXiv preprint arXiv,2014:1404,5331.
[13]TRACY C A,WIDOM H. On orthogonal and symplectic matrix ensembles[J]. Communications in Mathematical Physics,1996,177(3):727-754.
[14]BAI Z D. Methodologies in spectral analysis of large-dimensional random matrices,a review.[J]. Statist. Sinica,1999,(3):611-677.
[15]金明,李有明,高洋.基于广义特征值的合作频谱感知方法[J].通信学报,2013,34(1):105-110.
[16]弥寅,卢光跃,关璐.特征值类频谱感知算法的仿真分析,西安邮电学院学报,2014,19(5):27-33.
[17]曹开田,杨震.一种新型的基于最大特征值的合作频谱感知算法[J].电子与信息学报,2011,33(6):1367-1372.
[18]卢光跃,弥寅,包志强,等.基于特征结构的频谱感知算法[J].西安邮电学院学报,2014,19(2):59-63.
[19]赵知劲,胡伟康,王海泉.基于双特征值极限分布的合作频谱感知算法[J].电信科学,2014,30(4):82-87.
Spectrum Sensing Algorithm Based on Estimated Covariance Matrix MME Detection
YAO Shao-lin,ZHANG Zheng-bao,XU Xin,LIU Guang-kai
(Ordnance Engineering College,Shijiazhuang,050003,China)
Abstract:Aiming at the problem that the inaccurate estimation of sample covariance matrix for the statistical covariance matrix could lead to poor detection performance of the MME detection algorithm while sampling data length is small,a spectrum sensing algorithm based on estimated covariance matrix MME detection is proposed. First,the OAS estimator is used to estimate the statistical covariance matrix of sampling data. Then,the eigenvalue decomposition for the estimated covariance matrix is made. Finally,the ratio of maximum eigenvalue and minimum eigenvalue is taken as the detection statistic,which overcomed the defects that the detection threshold of the traditional MME algorithm fluctuate sharply with the sampling point incearcing,improved the robustness of the detection threshold. Simulation results show that the proposed algorithm has a robust detection threshold. Meanwhile,the detection performance was improved by 1 dB~2 dB.
Key words:cognitive radio,spectrum sensing,Maximum-Minimum Eigenvalue(MME),covariance matrix estimation,Random Matrix Theory(RMT)
中图分类号:TN92
文献标识码:A
文章编号:1002-0640(2016)05-0071-05
收稿日期:2015-04-19修回日期:2015-05-16
作者简介:姚少林(1992-),男,河南洛阳人,硕士。研究方向:认知无线电频谱感知。
