基于改进快速扩展随机树的机械臂路径规划

张云峰，马振书，孙华刚，陆继山

（1军械工程学院，石家庄　050003；2军械技术研究所2室，石家庄　050003）



基于改进快速扩展随机树的机械臂路径规划

张云峰1，马振书2，孙华刚2，陆继山1

（1军械工程学院，石家庄050003；2军械技术研究所2室，石家庄050003）

摘要：针对机械臂路径规划问题，提出一种基于改进RRT算法的路径规划方法。改进RRT结合了目标偏置策略和贪婪生长策略的优点，在随机采样时，以一定概率使采样点偏置为目标节点，降低随机采样的盲目性，在目标节点方向上采用贪婪式扩展策略，增加随机树局部方向上的生长速度。RRT法规划路径结果并非最优，提出改进GPP法删除多余路径节点，优化机械臂运动路径。通过与Biased-RRT和Greedy-RRT数值仿真结果对比，证明了改进RRT在计算时间、迭代次数、扩展节点数上均优于以上方法。在机械臂两种典型工作环境中的仿真结果表明，使用该方法可以较好解决排爆机械臂避障路径规划问题。

关键词：路径规划，快速扩展随机树，RRT，机械臂，最优路径

0　引言

机器人路径规划是机器人学的重要议题，它自20世纪70年代提出以来，逐渐成为人们的研究热点。机械臂路径规划是其中的重要内容，机械臂路径规划方法主要有细胞分解法［1］（Cell Decomposition）、人工势场法［2］（Artificial Potential Field）、随机路标法［3］（PRM，Probabilistic Roadmap）和快速扩展随机树法［4-6］（RRT，Rapidly-exploring Random Tree）等。

细胞分解法等基于静态地图分析的方法需要大量计算内存且不适用于动态环境中的路径规划。人工势场法可以实时在线规划，但容易陷入局部最小值，算法效率较低。近年来，基于随机采样的方法如PRM和RRT，越来越多地被用于机器人路径规划问题中［7-8］。RRT算法基本思想为在样本空间中随机采样并不断扩展树状结构直至到达目标，可适用于高维空间中的路径规划问题，但其随机采样的方式使节点遍布于整个采样空间，随着采样空间增长其计算效率会降低。Dmitry Berenson［9］使用Cost-RRT的方法引导随机树向代价低的方向生长，从而增加通过狭窄障碍的成功率并提高了算法效率。Piet Stroeven［10］、Wei Wang［11］等提出了多树同时扩展的方法，提高了RRT算法在样本空间中的扩展效率。Rahul Kala［12］根据随机采样的思想发展了RRG算法，变树状结构为图结构。为提高随机树在局部区域的生长速度，周芳等［13］提出了贪婪式生长方法（Greedy-RRT），提高了随机树的扩展效率。徐娜等［14］引入目标偏向的思想（Biased-RRT），减小了在全局状态空间均匀采样耗费的代价。但贪婪算法和目标偏置算法的固有缺点导致树的盲目生长和低效扩展，同时RRT算法的路径并非最优结果的问题没有得到解决。

本文针对某型机械臂路径规划的问题，提出了改进RRT算法，通过数值仿真与基本RRT、Greedy-RRT、Biased-RRT和改进RRT算法进行比较，并提出改进GPP法（Global path pruning）优化机械臂运动路径，最后在两种典型工作环境中通过虚拟样机仿真验证方法的有效性。

1　问题描述

研究机械臂的路径规划问题，首先要对机械臂和障碍物进行简化，研究它们之间的碰撞条件。本文以某型机器人6关节机械臂为研究对象，其中5个转动关节，1个棱柱关节，机械臂末端位置由棱柱关节和3个转动关节决定，因此，该机械臂虽为六自由度机械臂，但却是一种冗余结构。机械臂的D-H坐标系如图1所示，其D-H参数如表1所示。

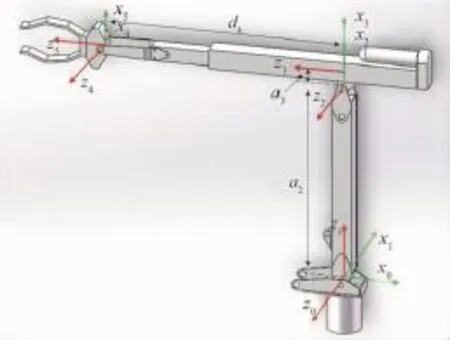
图1　机械臂示意图

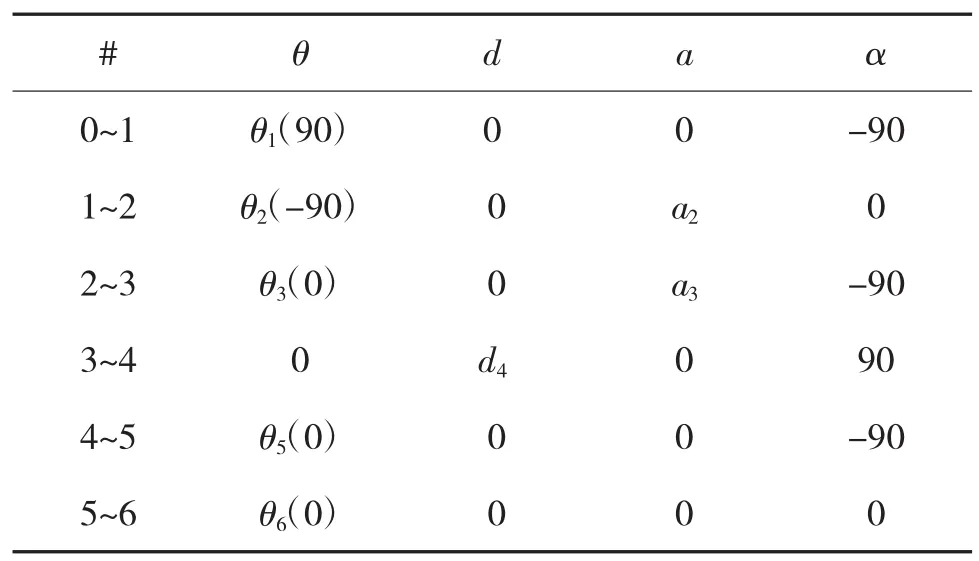
表1　机械臂D-H参数

本文使用几何包络法简化机械臂与障碍物的碰撞模型，如图2所示，机械臂连杆由圆柱体完全包裹，障碍物由多个球阵列包裹，最终机械臂与障碍物的碰撞检测问题变成一系列判断球心到圆柱中心线距离的问题。若球心到圆柱体中心线的距离小于球与圆柱体半径之和，则出现机械臂与障碍物干涉。该模型简化方法会损失一部分机械臂运动的自由空间，但简化了碰撞模型，提高了计算效率。

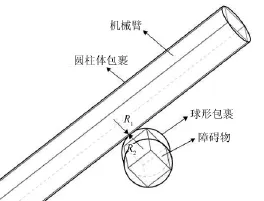
图2　模型简化示意图

为避免计算过程中多次调用迭代法求排爆机械臂逆运动学解［15］，本文采用J空间（Joint Space）中随机采样后通过正向运动学映射到C空间（Configuration Space）中检测碰障并规划路径的方法。J空间由所有可能关节角度的集合构成，C空间则是机械臂所有可能位姿的集合。Cobs空间表示因障碍物遮挡，机械臂不可到达的位姿集合，则Cfree空间｛Cfree=C/Cobs｝为自由空间，路径规划即在J空间找到一条映射到Cfree空间中的路径Γ（0，1），使得Γ（0）= Nstart，Γ（1）=Ngoal。

2　基于改进扩展随机树的路径规划

2.1RRT算法基本原理

RRT是一种基于随机采样的快速搜索算法，它把采集到的随机样本存储于一个树状结构中，并继续向未知空间搜索，直到接触目标点为止。基本RRT算法的过程如图3所示，红色区域为障碍空间，空白区域为Cfree空间。首先以初始节点Nstart作为树根，随机采样得到Nrand；然后找到随机树中离Nrand最近的节点Nnearest，在方向上以一定步长生成新节点Nnew，判断Nnew是否碰障，若否，则加入随机树，若碰障如节点1，则重新采样；最后，若随机树生长至目标节点Ngoal处，则算法结束，否则继续生长。为满足机械臂的运动学和动力学条件，以式（1）、式（2）生成新节点。其中J为机械臂的雅可比矩阵，它随关节位置的改变而改变，△q为关节改变量，q˙为机械臂的控制输入变量并在一定范围内取值，△t为时间步长。

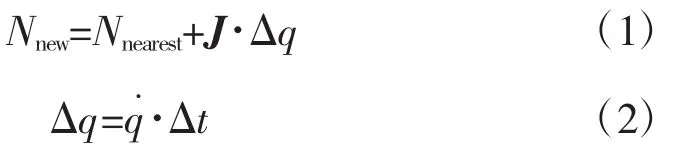
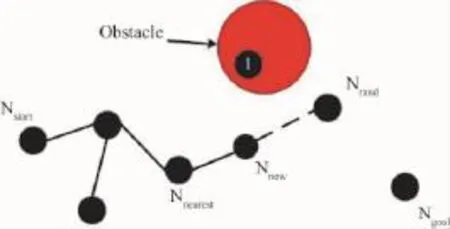
图3　基本RRT原理

采用基本RRT在3维空间中规划机械臂路径，结果如图4所示，为表示清晰，画面上只显示了机械臂末端位置，并未显示连杆机构，图4（a）、图4（b）、图4（c）分别为x-y、x-z、y-z视角。图中红色实体即为障碍物，蓝色树状图为随机树，青色节点为Nstart，绿色节点为Ngoal。路径规划结果用红色线段连接，可以看到，树状图的节点和边都绕开了障碍，证明了碰障模型的有效性。但基本RRT法采样具有盲目性，节点分布于机械臂整个工作空间中［16］，降低了算法的效率。

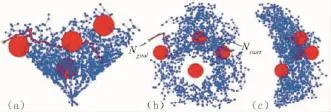
图4　基本RRT路径规划

2.2目标偏置策略和贪婪策略

针对RRT算法的盲目性问题，文献［12］引用了Biased-RRT算法，在随机树生长过程中以p为偏置概率使Nrand等于Ngoal，以（1-p）的概率随机产生Nrand。该方法实际上变随机搜索为相关于p的目标最优搜索，使随机树以概率p向目标节点生长，同时以概率（1-p）随机采样以避开障碍。P的取值决定搜索过程和搜索结果，当障碍物密集时P应较小，反之P取值较大。采用Biased-RRT规划机械臂空间路径，P取0.2，结果如图5所示，图5（a）为理想情况，由于加入了偏置概率，Biased-RRT所需节点数更少，提高了搜索效率。但其搜索过程中局部方向连续扩展能力不足，也会出现图5（b）所示的一般情况，随机树依然搜索了整个自由空间。

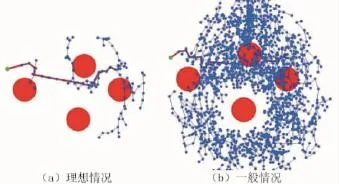
图5　Biased-RRT路径规划

传统RRT与Biased-RRT局部扩展速度较慢，为提高树枝生长速度，文献［11］提出了一种贪婪算法，在节点扩展时，若生成的新节点不与障碍物干涉，则在该方向上继续扩展节点，直到碰障或达到运动学极限。采用Greedy-RRT规划机械臂运动路径，结果如图6所示，由于贪婪算法特殊的节点生长方式，其树图具有不同的形态，每一树枝都较长，由于关节在特定方向上连续转动而使末端图像呈现螺旋形，Greedy-RRT以这种方法快速扩展至整个Cfree空间，如图6（b）。但其扩展具有盲目性，算法结果不稳定，图6（a）为较理想的情况，扩展过程中Nrand正好位于近似Ngoal方向，因此，减小了扩展节点数量。

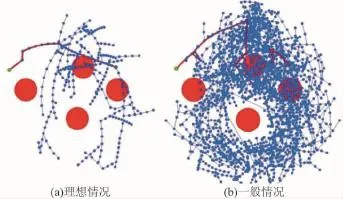
图6　Greedy-RRT路径规划结果

2.3改进RRT路径规划

通过上面的分析，Biased-RRT会使随机树向目标方向生长，减小了采样盲目性，Greedy-RRT会加快随机树在局部区域的扩展速度，增加算法效率。结合两者的优点，随机树生长过程中以偏置策略采集样本，当Nrand以概率p等于Ngoal时启用贪婪策略快速扩展该方向上的树枝，此时相当于目标最优搜索，在与目标距离的梯度方向上快速扩展随机树。而当Nrand随机采样时，不进行贪婪扩展，减少迭代次数，保留随机采样跳出局部最小值的能力。通过这种结合方式，改善了贪婪算法在不需要的区域扩展大量节点和偏置算法局部生长速度慢的缺点，改进RRT算法的伪码如下：

Algorithm.1：Improved-RRT Initialize（rrt）Add（rrt，Nstart）While Distance（Nnew，Ngoal）＞Dim p=rand If p＜=Biased Parameter Nrand=Ngoal Else Sampling（Nrand）End If NearestNode（rrt，Nrand）GenerateNew（Nnearest，Nrand）If～CollisionCheck（obs，Nnew）Add（rrt，Nnew）While Nrand=Ngoal GreedyExtend（rrt，Ngoal，Nnew）End While End If End While Add（rrt，Ngoal）Return rrt TracePath（rrt）

（1）初始化树状数据结构，把起始节点Nstart作为树根加入随机树中。

（2）在J空间中以目标偏置策略采集样本，即以概率p使随机节点Nrand等于目标节点Ngoal，以概率（1-p）随机采样。

（3）搜索树中与Nrand距离最近的节点Nnearest，在方向上以一定步长生成新节点，利用正向运动学计算机械臂各个连杆位姿，进行碰撞检测，判断其是否位于Cfree空间中。若是，把Nnew加入树中，若否，返回（2）重新采样。

（4）若Nrand等于Ngoal且Nnew不碰障，则采用贪婪扩张策略，在方向上不断生长新节点并加入树中，直至碰障或超出机械臂运动学限制。

（5）判断Nnew与Ngoal的距离，若小于距离极限Dim，则认为随机树已经扩展至Ngoal，把Ngoal加入树中，回溯父子节点关系，返回随机树和规划路径，若距离大于Dim则树继续生长。

图7为改进RRT路径规划结果，图7（a）为理想情况，随机树扩展碰障后快速找到目标节点方向，再次贪婪扩展，快速到达了目标节点。图7（b）为一般情况，随机树贪婪扩展遇到了障碍，此时由于以概率（1-p）多次随机采样，最终能够找到避障路径，跳出局部最小值，再次贪婪扩展得到一条无碰路径。与前述方法直观比较可知，改进RRT算法扩展节点更少，提高了算法效率。

图7　改进RRT路径规划

表2为使用4种RRT方法经过30次数值仿真试验后的对比结果。为在相同条件下比较算法效果，本文统一使用单树RRT，通过对比可以看到，由于加入了目标位置信息，Biased-RRT所用的计算时间和迭代次数均优于基本RRT。Greedy-RRT最终得到的随机树节点数与基本RRT相当，但所需计算时间和迭代次数则少得多，证明了Greed-RRT具有局部快速扩展能力。而改进RRT算法由于结合了Biased-RRT和Greedy-RRT两者的优点，在计算时间，迭代次数和扩展节点数上均优于前三种方法，证明改进RRT具有较高的计算效率。

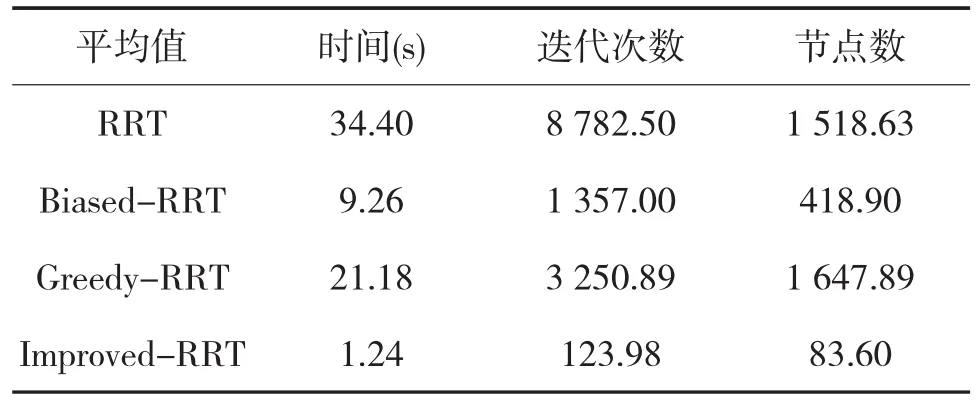
表2　数值仿真结果对比

3　路径优化

3.1改进GPP法

RRT法的优点是计算效率高，但由于其在全状态空间随机搜索可行路径，路径规划结果并非最优。大量多余节点导致路径长而曲折，必须删除规划结果的多余节点。节点删除通常有LOS（Line of sight path pruning）和GPP两种方法，GPP克服了LOS短视的缺点且有较高的计算效率，因此，采用GPP法删除多余节点。传统GPP方法主要针对二维环境下移动机器人的路径优化，改进GPP使其适用于三维条件下机械臂的运动路径优化：

（1）初始化优化路径Opath为空集用以存储优化路径，令BNode为Nstart，ENode为Ngoal，并把BNode加入Opath。

（2）判断BNode、ENode间运动路径是否碰障，若是，令ENode等于前一个节点，若否，把ENode加入Opath并令BNode等于ENode，ENode等于Ngoal开始下一轮循环，当Opath包含Ngoal时算法结束。

如图8所示，为判断BNode、ENode间路径是否碰障，在BNode、ENode间使关节定步长运动生成St个过渡节点，判断每个节点对应的机械臂构型是否碰障，通过这种方法把判断复杂曲面与球体是否干涉转化为判断若干不连续的线段与球体的位置关系，简化了碰障检测过程，其中St由式（3）求得：

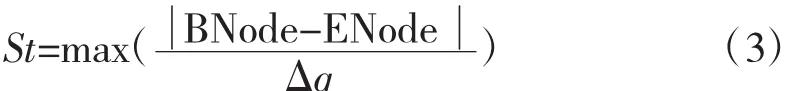
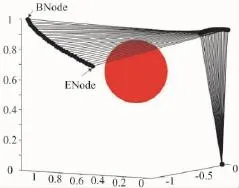
图8　GPP法示意图

3.1路径优化结果

使用GPP法删除某次路径规划结果的多余节点，如图9（a）所示，红色曲线为原始路径，包含29个节点，路径的笛卡尔空间长度和关节总运动量为2.910 1 m和4.233 5 rad（0.744 7 m），绿色曲线为优化后的路径，仅包含4个节点，路径的笛卡尔空间长度和关节总运动量为2.181 9 m和3.839 7 rad （0.621 0 m），分别为前者的75.0%和90.7%（83.4%），可以看到节点删除后路径的笛卡尔空间长度和关节运动量都得到大幅优化。图9（b）为机械臂沿优化路径运动示意图，可以清楚看到连杆结构的运动轨迹，优化后路径与障碍物并不干涉，证明了改进GPP的有效性。

图9　路径优化结果

4　仿真实验

为检验改进RRT算法路径规划的效果，对机械臂在两种不同环境下的路径规划结果进行运动学仿真。利用Solidworks建立机械臂虚拟样机模型与MATLAB生成的虚拟环境特征矩阵导入RecurDyn中，构建机械臂工作环境，保证了环境特征的一致性。使用MATLAB规划机械臂在两种环境中的工作路径，并把数值仿真结果导入RecurDyn中进行运动学仿真，使用MarkerTrace技术跟踪机械臂末端以观察其运动轨迹。

图10为稀疏障碍环境中机械臂路径规划仿真结果，该环境模拟机械臂在空旷环境中作业时可能遇到的树枝、岩石等稀疏障碍。图10（a）为初始位姿，在图10（b）、图10（c）中机械臂从上方绕过了黄色障碍物、绿色障碍物，在图10（d）中机械臂从前侧方绕过了粉色障碍物，最终到达目标位姿，图10（e）为目标位姿俯视图，图10（f）为目标位姿正视图。图中红色曲线为机械臂末端运动轨迹，可以看到机械臂良好地避开了所有障碍物，完成了从初始位姿到目标位姿的运动。

图10　稀疏障碍路径规划仿真结果

图11为狭窄通路障碍路径规划仿真结果，狭窄通路障碍环境模拟机械臂作业时可能遇到的车窗、车门、缝隙内有目标物的情况。图中蓝色有孔墙壁为障碍物模型，图11（a）为初始位姿，图11（b）为机械臂接近障碍运动轨迹，由于贪婪扩张策略，该段轨迹较为平滑。在图11（c）、图11（d）中机械臂接近墙面后与其保持一定距离的画面，由于算法以（1-p）的概率随机采样，机械臂得以避开墙体障碍。图11（e）、图11（f）为目标位姿的顶视图及正视图，可以看到机械臂的避障到达点的运动轨迹，机械臂较好地完成了通过狭窄通路障碍的任务。

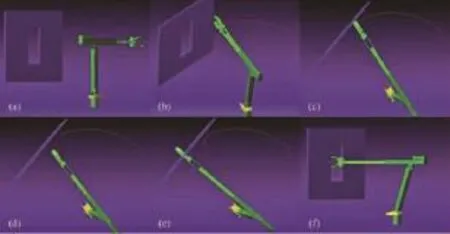
图11　狭窄通路障碍路径规划结果

5　结论

本文对比了传统RRT算法，Biased-RRT算法和Greedy-RRT算法在机械臂路径规划问题上的应用效果，结合它们的优点对RRT算法进行改进；针对RRT算法的不足，提出改进GPP法优化机械臂路径。在两种典型工作环境中的仿真结果表明，该算法可以有效规划机械臂运动路径，引导机械臂避障并完成任务。改进RRT算法的优点是效率高、节点扩展迅速、路径短且平滑，作为一种通用方法，它也可被应用于双树、多树以及带价树等其他RRT方法的节点扩展策略中，其中的路径优化方法也可用于PRM、RRT等路径规划方法的结果优化。

参考文献：

［1］TING Y，WEI W I，JAR H C. A path planning algorithm for industrial robots［J］. Computers&Industrial Engineering，2002，42：299-308.

［2］CONKUR E S. Path planning using potential fields for highly redundant manipulators［J］. Robotics and Autonomous Systems，2005（52）：209-228.

［3］RANTANEN M T. A connectivity-based method for enhancing sampling in probabilistic roadmap planners［J］. J Intell Robot Syst，2011，64：161-178.

［4］谢碧云，赵京，刘宇.基于快速扩展随机树的7R机械臂避障达点运动规划［J］.机械工程学报，2012，48（3）：63-69.

［5］JAILLET L，JOSEP M P. Path planning under kinematic constraints by rapidly exploring manifolds［J］.IEEE Transactions on Robotics，2013，29（1）：105-117.

［6］BERTRAM D，KUFFNER J，DILLMANN R，et al. An integrated approach to inverse kinematics and path planning for redundant manipulators［C］// IEEE International Conference on Robotics and Automation，2006：1874-1879.

［7］GERAERTS R，OVERMARS M H. Sampling and node adding in probabilistic roadmap planners［J］. Robotics and Autonomous Systems，2006，54：165-173.

［8］DASGUPTA B，GUPTA A，SINGLA E. A variational approach to path planning for hyper-redundant manipulators［J］. Robotics and Autonomous Systems，2009，57：194-201.

［9］BERENSON D，SIMEON T，SRINIVASA S. Addressing cost-space chasms in manipulation planning［C］// ICRA，2010：4561- 4568.

［10］STROEVEN P，LE N L，SLUYS L J. Porosimetry by double-random multiple tree structing in virtual concrete［J］. Image Anal Stereol，2012，31：55-63.

［11］WANG W，XU X，LI Y，et al. Triple RRTs：An effective method for path planning in narrow passages［J］. Advanced Robotics，2010，24：943-962.

［12］KALA R. Rapidly exploring random graphs：motion planning of multiple mobile robots［J］. Advanced Robotics，2013，27：1113-1122.

［13］周芳，朱齐丹，赵国良.基于改进快速搜索随机树法的机械手路径优化［J］.机械工程学报，2011，47（11）：30-35.

［14］徐娜，陈雄，孔庆生.非完整约束下的机器人运动规划算法［J］.机器人，2011，33（6）：666-672.

［15］介党阳，刘敬明，梁晓峰，等.机械臂技术在舰艇发射装置领域的应用［J］.四川兵工学报，2015，26（5）：20-23.

［16］ZHANG P F，MU X H，MA Z S. A PSGO-based method for inverse kinematics analysis of serial dangerous articles disposal manipulator［J］.Information-An International Interdisciplinary Journal，2012（12）：06-07.

［17］卞学良，杜清，马振书，等.危险弹药机器人机械臂运动学仿真分析［J］.现代制造工程，2010，32（6）：137-140.

Path Planning of Manipulators
Based on Improved Rapidly- Exploring Random Tree

ZHANG Yun-feng1，MA Zhen-shu2，SUN Hua-gang2，LU Ji-shan1
（1. Mechanical Engineering College，Shijiazhuang 050003，China；2. Ordnance Technology Institute，Shijiazhuang 050003，China）

Abstract：A certain improved rapidly -exploring random tree is proposed to solving the path planning problem of EOD manipulators. The improved RRT combines advantages of biased strategy and greedy strategy. By selecting goal node with some probability when sampling，improved RRT reduces the blindness of RRT. Greedy strategy is used for extending trees in the direction of goal node to enhance the extending rapid. The results by RRT are not optimal，an improved GPP technique is developed to prune the redundant nodes of planned paths，optimize the motion path of manipulators. By comparing the numerical simulation results of Biased-RRT and Greedy-RRT，the high efficiency of improved RRT is proved in computation time，iterations and number of extended nodes. The simulation results in two typical environments show that the algorithm can achieved path planning tasks well in obstacle circumstances.

Key words：path planning，rapidly-exploring random tree，RRT，manipulators，optimal path

中图分类号：TP241.3

文献标识码：A

文章编号：1002-0640（2016）05-0025-06

收稿日期：2015-03-15修回日期：2015-05-20

*基金项目：国家“863”计划基金资助项目（2001AA422420）

作者简介：张云峰（1991-），男，河北无极人，硕士。研究方向：机器人运动规划。