聚四氟乙烯/芳纶破斜纹织物衬垫拉伸性能数值仿真

2016-07-12王占山吕利叶张佳丽杨育林张芳芳

纺织学报 2016年7期

王占山，吕利叶，张佳丽，杨育林，张芳芳

(1. 燕山大学机械工程学院，河北秦皇岛 066004； 2. 燕山大学自润滑关节轴承共性技术航空科技重点实验室，河北秦皇岛 066004； 3. 全兴工业研发(廊坊)有限公司，河北廊坊 065000)

王占山1，2，吕利叶1，2，张佳丽3，杨育林1，2，张芳芳1

为了解自润滑关节轴承织物衬垫的拉伸性能，对其拉伸性能进行了数值仿真与试验验证。通过进行切片试验，利用激光共聚焦显微镜观测纤维截面形态，对截面形貌轮廓尺寸进行测量计算，得到了纤维束的几何参数，利用ANSYS有限元软件建立了织物衬垫增强相单胞模型；基于复合材料细观力学方法和周期性边界条件，研究了织物衬垫拉伸性能，利用ANSYS得出了聚四氟乙烯(PTFE)/芳纶(Kevlar)混织破斜纹衬垫的拉伸弹性常数；并将数值仿真分析结果与拉伸试验结果对比，结果相差约20%，在误差允许范围内。

织物衬垫；细观模型；拉伸试验；有限元仿真

自润滑关节轴承的内外圈之间黏结一层自润滑材料，该自润滑材料的结构主要为织物衬垫形式。自润滑关节轴承是关节轴承的一种，其关键功能件为自润滑衬垫，自润滑衬垫的寿命与可靠性对自润滑关节轴承的重要性不言而喻[1-3]。

在研究计算中，随着织物结构的改变，衬垫的基础数据相应改变。获取这些数据的传统方式为物理试验，但是该方式耗时、耗力、成本高[4]。利用有限元法可以获得材料力学性能的更多信息，能够分析材料非线性过程的历史，便于分析材料摩擦磨损过程。目前，针对自润滑材料拉伸性能的研究已取得一些成果。Jaehyon Choi等[5]研究了机织复合材料单胞内裂纹演化机制，对单胞模型施加了面内的单轴拉伸及剪切载荷。沈雪瑾等[6]根据具体纤维结构建立了衬垫的弹性性能分析模型，但是仅仅适用于斜纹织物。

织物衬垫的细观结构决定了其弹性性能和强度，即决定了宏观性能。为了实现织物衬垫的性能优化，预测织物的细观结构对宏观性能的影响程度，需要采用细观力学的分析方法[7]。本文建立了接近真实状态的衬垫细观模型，预测了混合材料性能参数，并获得了纬向拉伸情况下的应力场和应变场，为后续磨损过程有限元模型的建立奠定了理论基础。

1 织物衬垫细观力学模型

试验所用混织破斜纹织物衬垫为外购，其经向纤维束是Kevlar49，纬向纤维束由PTFE与Kevlar49混织而成，固化基体是酚醛缩醛树脂。

织物衬垫本身的编织结构具有周期性，最小重复体积单元(单胞，RVE)反映衬垫的整体性能，单胞结构示意图如图1所示。

1.1 织物组织截面形貌

1.2 织物衬垫几何模型

根据织物衬垫截面的实际形貌特征，依据Peirce模型[8]，使用文献[9]提出的任意压扁系数下的椭圆形截面建模方法，并结合1.1切片试验测量数据，得到织物衬垫纤维束相关参数，图4示出织物纬向截面几何结构示意图。图5示出破斜纹衬垫增强相单胞模型。相关几何参数详见表1。

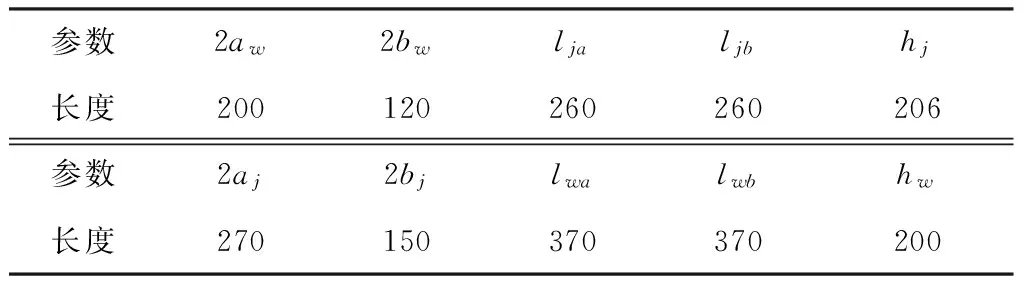
Tab.1 Section parameters of warp and weft fibers of broken twill liner μm

注：aj、bj、aw、bw分别为经向长短半轴长和纬向长短半轴长，lja、ljb分别为经向纱线交叉区域长度和非交叉区域长度，lwa、lwb分别为纬向纱线交叉区域长度和非交叉区域长度，hj、hw分别为经纬纱的屈曲波高。

由图5可以看出，在经纬纤维束交叉处，纤维束之间并没有相互接触。这是由于建立模型时，接触会产生干涉问题，因而进行了简化，在误差允许范围内对参数进行适当处理，获得近似模型。

2 织物衬垫拉伸力学性能

2.1 有限元计算结果及分析

纤维束的性质取决于单丝的性质，不同厂家生产的单丝的性能不尽相同。根据厂家提供的参数，运用Chamis模型[10]，使用式(1)计算纤维束的性能参数。纤维束及基体性能参数如表2所示。

(1)

式中：Ef1、Gf1分别为纤维方向的弹性模量和剪切模量，GPa；Ef2、Gf2分别为垂直于纤维方向的弹性模量和剪切模量，GPa；μf12为纤维方向泊松比；vf为纱线填充系数，萃取法测定衬垫中树脂百分比得到，vf=80%；Em、Gm分别为基体的弹性模量和剪切模量，GPa；μm为基体的泊松比。

表2 纤维束及基体性能参数

最小重复单元单胞构成宏观织物衬垫，为使单胞的性能代表衬垫的整体性能，单胞边界处需满足位移连续条件和应力连续条件[11]。根据文献[10]提供的周期性边界条件公式，导出衬垫拉伸预施加的周期性条件，本文仅针对纬向拉伸进行探讨，对织物衬垫施加纬向方向的拉伸，即x方向的拉伸，预施加的周期性边界条件如式(2)所示。

(2)

式中k为位移系数。

增强相单胞由纤维束和基体组成，其中纤维束是PTFE纤维和Kevlar纤维，为横观各向同性材料。基体是酚醛缩醛树脂，为各向同性材料。纤维束形状较为规则，宜选用六面体单元用体积扫略的方式划分网格。纤维束单元为Solid45单元，根据Solid45单元特性，设定网格单元坐标系沿纤维屈曲方向，实现纤维束的横观各向同性。基体的形状非常不规则，无法选用六面体单元，宜选用带中间节点的四面体单元(Solid92单元)采用自由网格划分方式。织物衬垫增强相单胞网格图如图6所示。

根据式(2)施加边界条件，建立位移约束方程，进行有限元运算，x向拉伸边界条件下经纬纤维束应力云图如图7所示。

增强相单胞中，纤维束主要承受载荷，基体起固定的作用。从纤维束的应力云图中可以看出，经纬纤维束交织的位置为最大应力处，即最容易发生拉伸破坏。

利用APDL中ETABLE命令分别求出有限元模型每个网格单元的平均应力(平均应变)与单元体积，并赋予相应单元表中；将单元平均应力表(平均应变表)与单元体积表相乘，赋予相应数据表；并对数据表进行求和计算。等效平均应力与平均应变分别根据式(3)、(4)计算得到。

(3)

(4)

依照式(3)、(4)计算，得出x方向平均应力为2.260×107Pa，x方向平均应变为0.979 2%，y方向平均应变为0.597 3%，计算得出x方向拉伸弹性模量值为2.310GPa，泊松比为0.610。

2.2 拉伸试验

拉伸试验主要参考GB/T 3923.1—1997《纺织品织物拉伸性能：断裂强力和断裂伸长率的测定(条样法)》和GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》进行测试。

织物拉伸试验设备如表3所示。同时拉伸试验机应具有一定的稳定性，载荷波动较小，小于+1%；速度相对恒定，当速度较小(≤10mm/min) 时误差小于等于20%，当速度较大(>10mm/min)时误差小于等于10%。

表3 织物拉伸试验设备

准备试样：对满足要求的试样编号、划线，测量试样上工作段内的厚度和宽度，任取3处，求平均值。纬向试样尺寸如表4所示；将夹具和试样中心线应重合；施加破坏载荷5%的载荷消除间隙，保证整个系统处于正常工作状态；纬向拉伸，加载速度为20 mm/min，测量试样的拉伸载荷和断裂伸长量。

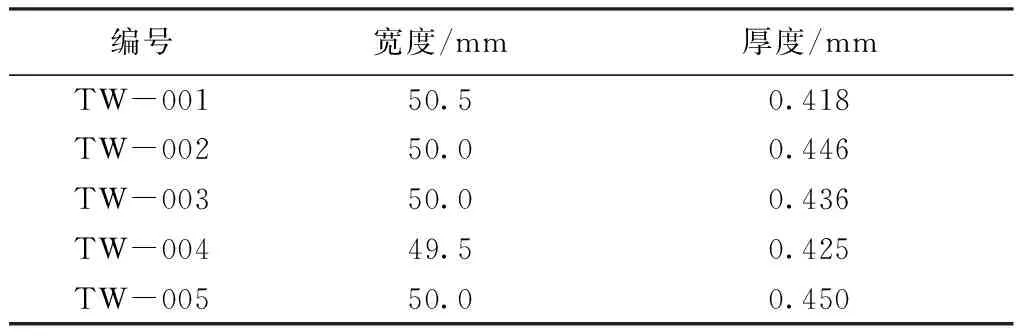
表4 纬向试样尺寸

2.3 试验结果及分析

5组纬向拉伸试验加载拉力与拉伸长度曲线如图8所示。

从图8可看出，拉伸初始阶段，载荷与位移为线性关系，此时衬垫完全处于弹性变形还未开始塑性变形。定义此直线段载荷增量值为△F，△F对应的标距L0内变形增量值记为△L，断裂时断裂伸长量记为△Lb，表5示出纬向试样拉伸弹性模量测量数据。表6示出纬向试样泊松比测量数据。

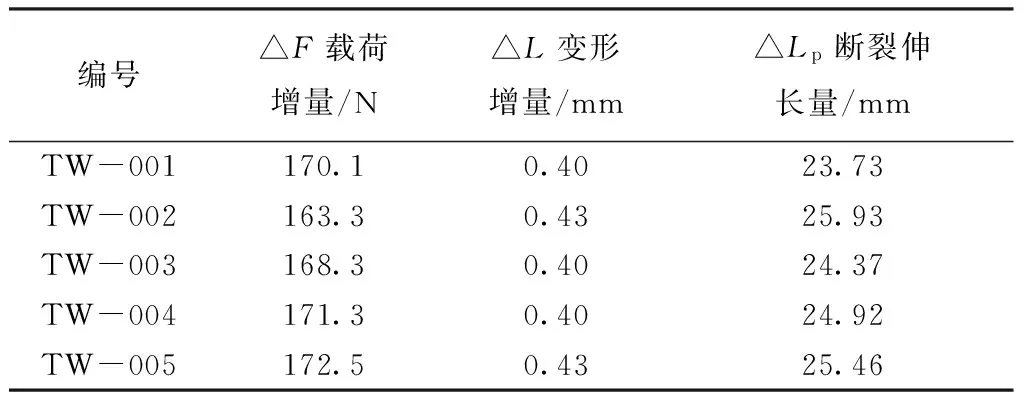
表5 纬向试样拉伸弹性模量测量数据

表6 纬向试样泊松比测量数据

将试验结果按照式(5)、(6)进行处理，得到弹性模量、泊松比的试验结果，如表7所示。设织物纬纱方向为主轴1方向，经纱方向为主轴2方向，垂直纱线方向为主轴3方向，根据表6中的结果得到平均弹性模量、泊松比。将有限元结果与实验结果对比，如表8所示。

(5)

(6)

式中：Et为拉伸弹性模量，MPa；b、d分别为试样宽度与厚度，mm；μ为泊松比；ε1为与载荷增量△F对应的轴向应变，ε1=△L1/L1；ε2为与载荷增量△F对应的横向应变，ε2=△L2/L2；L1、L2分别为轴向和横向的测量标距，mm；△L1，△L2分别为与增量△F对应的标距L1、L2的变形增量，mm。

表7 纬向拉伸试验结果

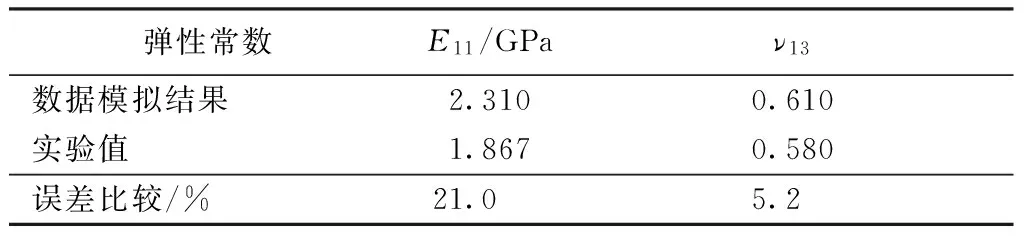
表8 有限元模拟结果与试验结果对比

由表8可看出，有限元结果与试验结果不完全一致，存在可接受的误差，总结原因有以下几点：1)衬垫几何模型建立时存在误差，为防止经纬纤维束之间产生干涉，模型中的纤维束不能接触，与实际情况存在差距；2)经纬纤维束的力学性能参数如弹性模量等是通过经验公式和将基体平均化推导出来的，与实际情况存在差异；3)试验过程与真实情况也存在一定误差，如试样测量、试验操作等。综上所述，在竭力减少误差存在的可能性时，有限元结果与试验结果存在一定误差是可以接受的。

3 结论

针对织物衬垫采用度验手段观测衬垫形貌，并依据Peirce模型，建立织物衬垫的椭圆形截面模型，并建立有限元模型，利用有限元技术进行静力拉伸仿真；利用试验方法检测衬垫拉伸性能参数，实验与仿真实验结果对比，得到破斜纹Kevlar/PTFE混织衬垫纬纱拉伸弹性模量仿真结果与试验结果相差约20%；泊松比仿真结果与试验结果相差5.20%。本文用混织破斜纹织物衬垫进行仿真，验证了织物衬垫细观力学模型的正确性，该模拟方法可推广到其他类型的织物衬垫，可为以后进一步研究衬垫性能提供基础，为研究织物衬垫摩擦磨损性能奠定了基础。

FZXB

[1] SAUTTER S, HADEN H, KOTTWITZ B. Spherical plain bearings for on and off road vehicles[J]. Bearing Technology: Analysis, Development and Testing, 1985: 11-26.

[2] 杨育林, 祖大磊, 黄世军. 自润滑关节轴承现状及发展[J]. 轴承, 2009(1):58-61. YANG Yulin, ZU Dalei, HUANG Shijun. Status and development of self-lubricating spherical plain bearings[J]. Bearing, 2009(1): 58-61.

[3] 沈雪瑾, 曹磊, 陈有光, 等. 织物衬垫自润滑关节轴

承的研究现状与展望[J]. 轴承, 2009(3):57-61. SHEN Xuejin, CAO Lei, CHEN Youguang, et al. Research Status and Prospect of Spherical Plain Bearings with Self-Lubricating Fabric Liner[J]. Bearing, 2009(3):57-61.

[4] 陈继刚, 薛亚红, 邱洪亮. 芳纶/聚四氟乙烯纤维织物衬垫力学建模与性能计算[J]. 纺织学报, 2015, 36(1): 82-87. CHEN Jigang, XUE Yahong, QIU Hongliang. Mechanics modeling and performance calculation of aramid/polytetrafluoroethene fabric liner[J]. Journal of Textile Research, 2015, 36(1): 82-87.

[5] JAEHYON C, KUMAR K. Woven fabric composites: part Ⅰ: predictions of homogenized elastic properties and micromechanical damage analysis[J]. International Journal for Numerical Methods in Engineering, 2001, 50: 2285-2298.

[6] SHEN Xuejin, LIU Yunfei, CAO Lei, et al. Numerical simulation of sliding wear for self-lubricating spherical plain bearings[J]. Journal of Materials Research & Technology, 2012, 13(1):8-12.

[7] 燕瑛. 编织复合材料弹性性能的细观力学模型[J].力学学报, 1997(4):429-438. YAN Ying. A micromechanical model for elastic behavior analysis of woven fabric composites[J]. Acta Mechanica Sinica, 1997(4): 429-438.

[8] PEIRCE FT. The geometry of cloth structure[J]. Journal of the Texitle Institute Transactions, 1937, 28(3): 45-96.

[9] 谷大鹏. 织物自润滑复合材料组元厚向分布研究及磨损试验表征[D]. 秦皇岛:燕山大学, 2013:33-37. GU Dapeng. Research on constituent distribution along with thickness of fabric self-lubricating composite and characterization of wear experiment[D]. Qinhuangdao: Yanshan University, 2013: 33-37.

[10] CHAMIS CC. Mechanics of composites materials- past, present and future[J]. Journal of Composites Technology & Research, 1989, 11(1): 3-14.

[11] 王新峰, 周光明, 周储伟, 等. 基于周期性边界条件的机织复合材料多尺度分析[J]. 南京航空航天大学学报, 2005, 37(6):730-735. WANG Xinfeng, ZHOU Guangming, ZHOU Chuwei, et al. Multi-scale analyses of woven composite based on periodical boundary condition[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2005, 37(6): 730-735.

Numerical simulation of tensile properties of polytetrafluoroethylene/Kevlar broken twill fabric liner

WANG Zhanshan1,2, LÜ Liye1,2, ZHANG Jiali3, YANG Yulin1,2, ZHANG Fangfang1

(1.CollegeofMechanicalEngineering,YanshanUniversity,Qinhuangdao,Hebei066004,China; 2.AviationKeyLaboratoryofScienceandTechnologyonGenericTechnologyofSelf-LubricatingSphericalPlainBearing,YanshanUniversity,Qinhuangdao,Hebei066004,China; 3.QuanxingIndustrialDevelopment(Langfang)Co.,Ltd.,Langfang,Hebei065000,China)

In order to understand the tension property of the fabric liner for self-lubricating spherical plain bearings, numerical simulations and experiment verification of the tensile properties were investigated. First of all, the section testing was performed, and laser scanning confocal micro-scopy (LSCM)was used to observe the section morphology of fibers. By measuring and calculating for the profile, the geometry parameters of the fibers were obtained. The reinforcementunit-cell model of the fabric liner was built using ANSYS finite element software. Then, based on the mesomechanics of composite materials and the periodic boundary conditions, the tensile properties of the fabric liner were studied and the tensile elastic constants of the hybrid polytetrafluoroethylene (PTFE)/Kevlar broken twill fabric liner were obtained using ANSYS. At last, comparison of the experimental results and the simulated ones shows that the error is about 20%, which is within the allowed range.

broken twill fabric liner; mesoscopic model; tensile testing; finite element simulation

10.13475/j.fzxb.20150605506

2015-06-28

2015-12-26

王占山(1986—)，男，博士生。主要从事自润滑关节轴承织物的性能研究。杨育林，通信作者，E-mail：yang_yulin123@163.com。

TB 332