老铁山—长兴岛VLCC外海航路安全水深的确定

李连博+刘德新+尹建川+戴冉

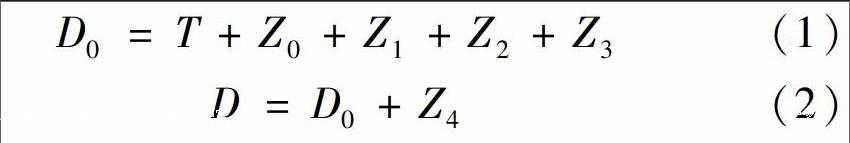
摘要：

为确保长兴岛北港区30万吨级油船泊位正常营运，科学合理地规划老铁山水道至长兴岛北港区的外海航路，对国内外关于航道水深的标准、规范和影响船舶富余水深的要素进行对比分析.基于MATLAB8.0平台，利用芳村公式、Eryuzlu（1994）修正公式和Norbin公式计算船舶在开敞水域航行时的下沉量、富余水深和安全水深，并画出满载VLCC在开敞水域航行时的下沉量、富余水深、安全水深在不同航速情况下随水深与吃水比值变化的曲线.根据《海港总体设计规范》、芳村公式、Eryuzlu（1994）修正公式和Norbin公式，计算出在开敞水域航行的满载VLCC在不同航速下所需的下沉量和外海航路安全水深.运用该方法提出老铁山水道至长兴岛北港区外海航路的安全水深建议值.该方法可为渤海湾其他有VLCC码头的外海航路设计提供一定的参考.

关键词：

超大型油船（VLCC）；航路规划；下沉量；富余水深；水深标准

中图分类号：U612.3

文献标志码：A收稿日期：20150913修回日期：20151116

0引言

大连长兴岛30万吨级油船码头工程位于长兴岛北港区东防波堤外侧，码头长436m，栈桥长318m，码头前沿水深25m，年设计通过能力1768万t.该工程规划中，仅对30万吨级油船码头进出港航道进行了详细的规划设计，外海航路只是建议采用该水域现有的超大型船舶习惯航路.[1]为确保长兴岛北港区30万吨级油船泊位正常营运，科学合理地规划老铁山水道至长兴岛北港区的外海航路是十分必要的.外海航路安全水深标准的确定是规划外海航路的首要工作，因此本文通过对近些年国内外关于航路水深及富余水深方面研究的分析、计算和对比，提出老铁山水道至长兴岛北港区外海航路安全水深的建议值.

1设计船型

根据《海港总体设计规范》（JTS165—2013）中关于设计船型尺度的内容，可得30万吨级油船的主尺度：总长为334.0m，型宽为60m，型深为31.2m，满载吃水为22.5m.

基于此，在劳氏船级社船舶数据库中提取50艘满载吃水为22.5m的超大型油船（VeryLargeCrudeCarrier，VLCC）的数据进行统计，得出设计船型数据：船舶载质量为318000t，满载排水量为362500t，船长L=333.5m，船舶垂线间长LBP=320.4m，型宽B=60m，满载吃水d=22.5m，型深D=30.4m，方形系数Cb=0.79，纵稳心高度为343m，横稳心高度为6.6m，重心与船中的距离为0.4m，重心与基线的距离为17.6m.

2国内外航路水深标准、规范和相关研究

2.1《海港总体设计规范》

根据《海港总体设计规范》（JTS165—2013）[2]规定，航道通航水深D0和航道设计水深D分别为

式中：T为设计船型满载吃水；Z0为航行时的船体下沉量；Z1为船舶航行时龙骨下的最小富余水深，根据规范中表格和海域实际情况，取0.6m；Z2为波浪富余水深，根据表格规范，取船、浪夹角为90°，前4%较大波的平均波高为2m，Z2为1.04m；Z3为船舶装载纵倾富余水深，杂货船、集装箱船可不计，油船、散货船均为0.15m；Z4为备淤富余水深，应根据两次挖泥间隔期的淤积量确定，不宜小于0.4m；各变量的单位均为m.

2.2在开敞浅水域航行时富余水深的确定

本文确定富余水深的方法是在考虑水深误差、无外界条件影响时的船体下沉量、受外界条件影响时的船体下沉量、浅水对船速的影响和安全操纵对富余水深的影响等因素的基础上，对比在开敞浅水域航行时的富余水深估算模型，选取适合本文计算用的富余水深估算模型[34].

2.2.1水深误差

水深误差主要受潮高误差δm，海图测量误差δs，海底底质附加值δb和堆积高度δa（这4个量的单位为m）的影响，因此水深可能存在的最大误差δh为

式中：P为实测大气压，hPa；Hc为海图水深，m.

对有泥沙淤积的沙河港口和航道，应在富余水深估算中计入δa（无堆积时δa取值0）.

2.2.2无外界条件影响时的船体下沉量

（1）无风浪时匀速航行中的船体下沉量.

国外关于下沉量的计算公式[5]主要有Hofft（1974）公式、Huuska（1976）公式、Eryuzlu（1978）公式、Barrass（1981）公式、Norbin公式、Millward（1990）公式、Millward（1992）公式、Eryuzlu（1994）修正公式、Ankudinov（1996）公式、芳村公式等.1974年Hofft提出Hofft公式，较为精确地计算了船体下沉量，但与实船实测数据仍有较大误差.Huuska以水动力数学理论为基础，运用拉普拉斯方程、边界条件进行傅里叶变换求取垂向力和纵倾力矩，进而求船首下沉量；该公式计算稳定，使用范围较广，但当航速较大时曲线会发生变形.1978年Eryuzlu在开敞水域通过油船实验提出了Eryuzlu估算公式，之后不断对该公式进行改进，估算的精确度逐渐提高.[67]1979年Barrass在实船实验和模型实验的基础上提出了船首下沉量简易估算公式，但考虑因素较少，其准确性有待进一步验证.[8]1986年Norbin在Tuck和Taylor公式基础上提出了适用于开敞水域Fr<0.4时的船体下沉量估算公式，该公式并不适用于所有大型船舶，但能够提供一定的参考.1990年Millward以细长体理论为基础提出Millward估算公式，结合7条船模实验结果进行分析，并对该公式进行改进，适用于较大型船舶，但仅以7条船模数据进行验证，其可靠性不足；芳村在Tuck公式基础上，结合实测数据对其进行变形，得到了芳村计算公式，该公式计算结果与实测数据较为接近，数据相对稳定，适用于各种船型，估算值普遍偏小.[910]表1给出了以上公式的具体适用范围[5].通过对以上下沉量公式的使用范围及特点的分析，选取芳村公式、Eryuzlu（1994）修正公式和Norbin公式对VLCC的下沉量进行计算.芳村公式