常微分方程中比较原理的应用
2016-07-11田苗青郜欣春郑州大学西亚斯国际学院文理学院河南新郑451150
田苗青 郜欣春(郑州大学西亚斯国际学院文理学院,河南新郑451150)
常微分方程中比较原理的应用
田苗青郜欣春
(郑州大学西亚斯国际学院文理学院,河南新郑451150)
摘要:在研究非线性系统问题时,比较原理起着举足轻重的作用。比较原理可以将研究非线性问题转化为线性问题,使问题简单化,并得到非线性问题解的一些重要性质,从而给研究这些非线性问题所对应的实际问题提供了理论依据。文章主要通过举两个简单的例子说明比较原理的用法。
关键词:比较原理;非线性系统;解的性质
一、预备知识
我们不加证明地引入比较原理,详细证明参见[1]中的引理3.4。
引理1.1(比较原理)考虑微分方程

其中t≥0,f(t,u)关于t连续,且关于u满足局部Lipschitz条件。设[t0,T)是u的最大存在区间,T可以是∞。如果对任意的t∈[t0,T),v=v(T)满足

则有v( t)≤ u( t), t∈[ t0, T )。
注:从引理条件可知(1.1)的解是存在的,结论说明满足微分不等式(1.2)的解可由(1.1)的解控制。
在研究复杂的非线性问题时,可以用比较原理将问题简化成可求解微分方程,从而得到非线性问题解的一些性质,给其对应的实际问题提供重要的理论依据。下面,我们举两个简单的例子来说明比较原理的用法。
二、应用举例
例1设u=u(t)对任意的t≥0满足
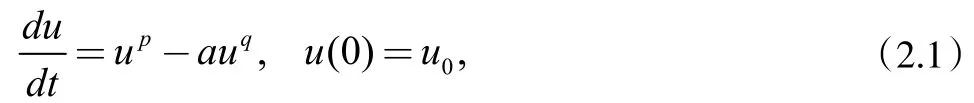
其中q>p≥1,a>0。证明:对任意非负初值u(0x),(2.1)的
证明:易证(fu)=up-auq满足局部Lipschitz条件,故对某t1>0(2.1)在[0,t1)有唯一解。
由u(0x)的非负性及比较原理,易知
由比较原理知,u≤v=u0,∀t≥0。
注:若在(2.1)中取p=1,q=2,则此方程就是经典的人口增长Logistic模型[2],从例子结果可以看出,人口不会无限制增长,是整体有界的。
例2设(u,v)满足方程组


注:方程组(2.2)用来分析生物系统中抑制性神经元和兴奋性神经元之间的交互作用,u,v分别表示兴奋性神经元和抑制性神经元的输出[4]。在此例中,虽然方程组(2.2)很复杂,但是我们通过适当地变换及比较原理,将问题转化成了易求解的一阶线性微分方程,从而得到我们想要的结果。
从以上两个例子中可以看出,在我们研究一些非线性问题时,不是直接求解所给的方程,而是通过比较原理转化为简单的方程去求解,从而得到我们想要的性质。可见,比较原理在研究非线性动力系统时起着至关重要的作用。
参考文献
[1][美]Hassan K. Khail.非线性系统[M].北京:电子工业出版社,2007:102-103.
[2][美]Franks R. Giordano,William P. Fox,Steven B. Horton.数学建模[M].叶其孝,姜启源,等译.北京:机械工业出版社,2014:335.
[3]丁同仁,李承治.常微分方程教程[M].北京:高等教育出版社,2004:31-34.
[4]Tonnelier A,Meignen S,Bosch H,and Demongeot J. Synchr onization and desychronization of neural oscillators[J].Neural Networks,1999,12:1213-1228.
Abstract:Comparison principle plays a crucial role in the study of nonlinear system,and the nonlinear problem is transformed into a linear problem through the principle. Thus,it is easy to solve and get some important properties of the nonlinear system,which helps to study the practical problem corresponding to the nonlinear model. This paper illustrates the use of the comparison principle through a few simple examples.
Keywords:compare principle;nonlinear system;properties of the solution
中图分类号:O175.14
文献标志码:A
文章编号:2096-000X(2016)11-0253-02
作者简介:田苗青(1981,1-),女,汉族,籍贯:河南省林州市,学历:硕士研究生,职称:讲师,职务:教师,研究方向:非线性发展方程。
