基于希尔伯特-黄变换的电力系统小干扰稳定分析方法

李雨

(广西电力系统最优化与节能技术重点实验室，广西 南宁 530004)



基于希尔伯特-黄变换的电力系统小干扰稳定分析方法

李雨

(广西电力系统最优化与节能技术重点实验室，广西 南宁 530004)

摘要：采用特征值求解分析系统小干扰稳定时存在不足：全部特征值的求解在大规模电力系统中会出现“维数灾”；分析大规模系统的部分特征值求解方法可能遗漏某些重要的模态。为此，提出一种基于时域特性曲线分析的电力系统小干扰稳定分析方法。该方法基于矩阵指数函数的计算，获得表征系统小干扰稳定性的时频特性曲线，通过希尔伯特-黄变换(Hilbert-HuangTransform，HHT)方法分析该时频特性曲线获取系统的模态参数，进行小干扰稳定分析。最后，通过WSCC3机9节点系统算例验证了该方法的有效性。

关键词：电力系统；时域仿真；矩阵指数计算；小干扰稳定分析；希尔伯特-黄变换

现代电力系统逐步向超大型互联电力系统发展，电网负荷需求逐年增加、输电线路的输送功率不断增大，电力系统的运行条件变得日益紧张，小干扰稳定问题频繁出现，已经成为制约联络线功率传输和互联电网安全稳定运行的重要因素[1-2]。

常用的计算小干扰稳定的方法是基于状态矩阵的特征值计算，通过判断特征值实部在负半轴的情况说明系统的小干扰稳定性。计算特征值的方法有QR法(利用矩阵的QR分解，逐步按递推法构造矩阵分解序列的过程，其中Q为正规正交矩阵，R为上三角形矩阵)，其鲁棒性强，收敛速度快，但不能稀疏实现，因而不能适应于大规模电力系统的小干扰稳定性分析[3]。对于大规模电力系统，QR计算方法存在“维数灾”，很多学者对关键特征值的求解进行了研究。文献[4]提出了一种借助Cayley变换将关键特征值计算变为主特征值计算的方法，导出了基于稀疏增广状态矩阵的幂法迭代公式；文献[5]应用Jacobi-Davidson方法求取系统状态矩阵的关键特征子集，使用了电力系统线性化模型中的增广状态矩阵进行相应面向稀疏的计算。文献[6]把Krylov-Schur方法应用于大规模电力系统的小干扰稳定性分析，求取状态矩阵阻尼比最小的部分特征值。这些方法只计算一部分对稳定性判别有关键影响的特征值，以确保计算精度和速度都可以满足大规模电力系统的要求，但不能保证所有负阻尼和弱阻尼模式不被漏掉。为了避免特征值直接求解的不足，本文应用小扰动后系统的时频特性，直接获取状态矩阵的迹的轨迹，从而获取系统的振荡参数，分析系统稳定性。获取状态矩阵的迹的轨迹就是对状态矩阵进行指数计算，在矩阵指数计算常用的数值方法中，缩放平方法因其更少的矩阵乘法和开方计算而具有更高的计算效率和准确度。

电力系统运行过程中，小干扰失稳多体现为低频振荡问题，衡量机电振荡模式有2个常用指标：衰减系数σ和阻尼比ζ。ζ计及了振荡频率，因此使用起来更为方便，目前ζ已成为衡量小干扰稳定性最主要的指标[7]。对于实际电网，机电振荡模式下ζ应达到多少并没有统一定义，其典型值的大致范围为0.02～0.05。

李雨：基于希尔伯特-黄变换的电力系统小干扰稳定分析方法希尔伯特-黄变换(Hilbert-Huang Transform，HHT)方法用于分析振荡信号时，既能处理线性、平稳信号，又能处理非线性、非平稳信号，是一种可以根据信号的局部时变特征进行自适应时频分解的分析方法。本文采用HHT方法对系统迹的轨迹进行自适应分解，得到相关时频分量，并对每个分量经过Hilbert变换计算出振荡频率、阻尼比ζ等系统的振荡特性参数，然后根据与系统小干扰振荡的对应关系将这些参数转换成系统的关键模态值，从而反映出系统的小干扰稳定情况。最后，本文在WSCC 3机9节点系统算例中验证该方法的有效性。

1小干扰稳定分析一般性描述

在描述电力系统动态特性的微分-代数方程上根据李雅普诺夫线性化理论，在系统平衡点进行线性化，得到小干扰稳定的微分代数方程：

(1)

对式(1)消去运行向量Δy得：

(2)

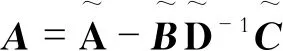
基于线性定常时不变系统的时域解，则式(2)的时域解

(3)

式中Δx(0)为系统自由运动的初始状态。

设λ、v、uT分别表示状态矩阵A的特征值及对应的右向量、左向量，文献[3]给出了式(3)对应的原始状态向量的时域解

(4)

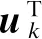
基于式(3)、(4)可知

(6)

式中tr(*)为矩阵的迹。

令y(t)=tr(eAt)，则y(t)表示了所有特征值的指数函数线性和。

2缩放平方法

对于矩阵指数的求解方法，文献[8]应用精细积分法求解，文献[9]给出了19种求解方法，其中缩放平方法是应用最广泛有效的求解方法。其以2的幂次缩放矩阵来使得矩阵的范数减少到1阶，同时应用Padé逼近来获取矩阵指数的近似值，然后重复平方来撤销缩小的效果[10]。该方法应用表达式为

(7)

(8)

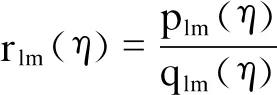
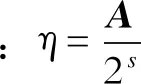
3HHT理论

3.1经验模态分解

HHT方法的核心部分在于经验模态分解(empirical mode decomposition，EMD)过程，在这个过程中定义了使得进行Hilbert变换求取的瞬时频率具有物理意义的固有模态函数(intrinsic mode function，IMF)信号。IMF信号满足以下两个条件[11-12]：条件一，在所有的分析数据段，极值点的个数和零点的个数必须相等或差值至多为1；条件二，在任意时间点上，分别由局部极大值点、局部极小值点形成的两条包络线的均值为零。但是第二个条件是很难达到的，研究者对此有不同的近似处理方法，在本文中IMF的筛选条件采用的是法国学者G-Rilling于2003年提出的基于模态幅值和估计函数的改进准则[12]。

EMD分解的具体步骤：

a)找到原始信号s(t)的所有极大值和极小值点，分别用三次埃尔米特插值函数得到s(t)的上、下包络线emax(t)、emin(t)；

c)将h(t)作为新的s(t)，重复步骤a)、b)，直到h(t)满足IMF条件则停止，此时得到第一阶IMF记作c1(t)；

d)将r(t)=s(t)-c1(t)作为新的s(t)，重复步骤a)、b)、c)，依次得到第二阶IMF、第三阶IMF，……，最终可得：

(10)

式中：ci(t)为第i个IMF分量；r(t)为剩余量。

① 估计函数β(t)∈(θ1,θ2)，θ1、θ2分别为估计函数数值的上下限，θ1、θ2一般取值0.05、0.5。

② 满足条件①的序列数与总序列数的比值达到1-α，α为可根据需要设置数值的变量，α一般取值0.05；

③ 过零点数和极值点数相等或相差1。

分解终止条件，应用的是Huang[13]等人在提出EMD分解的同时给出的分解终止条件。

3.2Hilbert变换

对任一上述分解得到的IMF信号ci(t)，Hilbert变换为

(11)

式中τ为积分变量。

即可获得解析信号

(12)

式中：a(t)为信号的瞬时幅值；φ(t)为信号的瞬时相位。

从而信号的瞬时幅值a(t)、瞬时相位φ(t)和瞬时频率f(t)的计算如下：

3.3小干扰稳定信息的提取

一个振荡模式λ1,2=σ±jω可以表达为

(14)

式中：A0为b(t)的幅值；ω为角速度；φ为相位。

其响应特性

式中ω0为初始角速度。

那么阻尼比

(15)

如果一个振荡信号x(t)是多个不同频率的振荡模式的线性和，即

(16)

该信号进行HHT转换得到

(17)

式(16)、(17)中：Ak为第k个模态的幅值；σk为第k个模态的衰减系数；ωk为第k个模态的角速度；φk为第k个模态的相位；ak(t)为第k个IMF信号的幅值；φk(t)为第k个IMF信号的相位。

则可知每个IMF分量对应一个振荡模式，通过求解IMF的幅值、频率可获得系统的模态参数。

4算例分析

本文采用WSCC3机9节点系统算例进行分析，其结构框架如图1所示，结构参数见文献[14]，发电机采用六阶模型。

文献[3]给出了详细的状态矩阵形成过程，本文不再叙述。由于系统都会存在一个0的特征值，其指数函数数值为常数1，所以不需要求解该特征值，就在获取的数值曲线上减去1。取仿真时长为10s，步长为0.05s，获得该系统的状态矩阵指数函数曲线y(t)如图2所示。

对y(t)进行EMD分解获得两个固有模态分量f1、f2以及剩余分量r，如图3所示。

按式(13)求解每个IMF的瞬时幅值、瞬时相位和瞬时频率。

由式(16)、(17)的对应关系得

(18)

式中：fi、σi、ζi分别为原信号不同频率分量的频率、衰减系数和阻尼比；fj、aj为每个IMF的瞬时频率和瞬时幅值。

对图3中的每个IMF分量的瞬时值进行最小二乘法拟合并应用式(13)和式(18)进行计算，获得IMF分量的频率、衰减系数和阻尼比参数(见表1)。

从表1可以知道原信号分解后获得两个振荡模式-1.099 0±j12.445 0(此处12.445 0=2πf)、-0.324 6±j7.709 0和一个衰减模态，阻尼比分别为0.088、0.042、1。与对该系统进行QR求解得到特征值的对照见表2。

表2本文方法与QR算法的比较

QR算法计算结果存在两个振荡模态，本文所提算法能较准确地判断系统的振荡模态。

5结束语

本文基于矩阵指数函数的计算，获得表征系统小干扰稳定性的时频特性曲线。通过HHT方法对该曲线进行分解转换，求解出每个分量的瞬时幅值、瞬时相位及瞬时频率。根据曲线特性与分解分量的关系计算出小干扰稳定分析的各模态参数，判定稳定性。本文的优点在于通过曲线获得振荡模态参数，避免大量特征值的计算，快速准确，为大系统小干扰稳定在线分析提供依据。

参考文献：

[1] 周双喜，苏小林.电力系统小干扰稳定性研究的新进展[J]. 电力系统及其自动化学报，2007，19(2)：6-15.

ZHOU Shuangxi，SU Xiaolin. Advance of Study on Small Disturbance Stability of Power Systems[J]. Proceedings of the CSU-EPSA，2007，19(2)：6-15.

[2] 邢洁，陈陈，武鹏.考虑小干扰稳定约束的有功优化调度[J]. 电力系统及其自动化，2010，34(12)：25-28.

XING Jie，CHEN Chen，WU Peng. Optimal Active Power Dispatch with Small Signal Stability Constraints[J]. Automation of Electric Power Systems，2010，34(12)：25-28.

[3] 王锡凡，方力良，杜正春. 现代电力系统分析[M]. 北京：科学出版社，2003.

[4] 杜正春，刘伟，方万良，等.小干扰稳定性分析中一种关键特征值计算的稀疏实现[J]. 中国电机工程学报，2005，25(2)：17-24.

DU Zhengchun，LIU Wei，FANG Wanliang，et al. A Sparse Method for the Calculation of Critical Eigenvalue in Small Signal Stability Analysis[J]. Proceedings of the CSEE，2005，25(2)：17-24.

[5] 杜正春，刘伟，方万良，等.基于JACOBI-DAVIDSON方法的小干扰稳定性分析中关键特征值计算[J]. 中国电机工程学报，2005，25(14)：19-24.

DU Zhengchun，LIU Wei，FANG Wanliang，et al. The Application of the JACOBI-DAVIDSON Method to the Calculation of Critical Eigenvalues in the Small Signal Stability Analysis[J]. Proceedings of the CSEE，2005，25(14)：19-24.

[6] 杜正春，李崇涛，潘艳菲，等.一种求取大规模电力系统关键特征值的有效方法[J]. 电力系统自动化，2014(2)：52-58.

DU Zhengchun，LI Chongtao，PAN Yanfei，et al. An Efficient Method for Computing Critical Eigenvalues of Large-scale Power Systems [J]. Automation of Electric Power Systems，2014(2)：52-58.

[7] 周小谦.我国“西电东送”的发展历史、规划和实施[J]. 电网技术，2003，27(5)：1-5.

ZHOU Xiaoqian. Development，Planning and Implementation of the Project of Power Transmission from West China to East China[J]. Power System Technology，2003，27(5)：1-5.

[8] CAI Guowei，LI Zhenxin，YANG D Y.Large-scale Power System Small Signal Stability Analysis Based on Matrix Exponential[J]. IEEE Transactions on Power System，2011，11(2)：1021-1025.

[9] MOLER C，LOAN C V. Nineteen Dubious Ways to Compute the Exponential of a Matrix，Twenty-five Years Later[J]. Society for Industrial and Applied Mathematics，2003，45(1)：3-49.

[10] HIGHAM N J. The Scaling and Squaring Method for the Matrix Exponential Revisited [J]. SIAM J. Matrix Anal. Appl.， 2005，26(4)：1179-1193.

[11] 李天云，高磊，赵妍.基于HHT的电力系统低频振荡分析[J]. 中国电机工程学报，2006，26(14)：24-30.

LI Tianyun，GAO Lei，ZAO Yan.Analysis of Low Frequency Oscillations Using HHT Method[J]. Proceedings of the CSEE，2006，26(14)：24-30.

[12] RILLING G，FLANDRIN P，GONCALVES P. On Empirical Mode Decomposition and Its Algorithms[J]. IEEE Transactions on Power System，2011，11(2)：1021-1024.

[13] HUANG N E，WU M-L C，LONG S R. A Confidence Limit for the Empirical Mode Decomposition and Hilbert Spectral Analysis [J]. Mathematical Physical & Engineering Sciences，2003，36(2)：2317-2345.

[14] SAUER P W，PAI M. Power System Dynamics and Stability[M]. Upper Saddle River，NJ：Prentice-Hall，1998.

AnalysisMethodforSmallSignalStabilityofPowerSystemBasedon

Hilbert-HuangTransformLIYu

(GuangxiKeyLaboratoryofPowerSystemOptimizationandEnergyTechnology,Nanning,Guangxi530004,China)

Keywords：powersystem;time-domainsimulation;matrixexponentialcalculation;smallsignalstabilityanalysis;Hilbert-Huangtransform(HHT)

Abstract：Therearedeficienciesofthesolutiontoeigenvalueforanalyzingsmallsignalstabilityofthepowersystemincludingdimensiondisastersofsolutionstoalleigenvaluesinlargescalepowersystemsandparteigenvaluesolvingmethodforlargescalesystemsbeinglikelytoleaveoutsomeimportantmodals.Therefore,thispaperproposesakindofanalysismethodforsmallsignalstabilityofpowersystembasedontime-domaincharacteristiccurveanalysis,whichisbasedoncalculationonmatrixexponentialtoobtainthetime-domaincharacteristiccurverepresentingsmallsignalstabilityofthesystem.Meanwhile,itisabletoobtainmodalparametersofthesystembyanalyzingthistime-domaincharacteristiccurvebasedonHilbert-Huangtransformmethodsoastoconductanalysisonsmallsignalstability.Finally,exampleanalysisonWSCC3machinewithninenodesverifiesvalidityofthismethod.

doi:10.3969/j.issn.1007-290X.2016.04.008

收稿日期：2015-10-12修回日期：2016-01-05

中图分类号：TM71

文献标志码：A

文章编号：1007-290X(2016)04-0045-05

作者简介：

李雨(1989)，女，广西桂林人。在读硕士研究生，主要研究方向为电力系统小干扰稳定分析与控制。

(编辑彭艳)