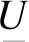SVC与TCSC优化配置在电力系统静态电压稳定中的应用
2016-07-11李娟许欣李壮庄海军齐永志高松
李娟,许欣,李壮,庄海军,齐永志,高松
(1. 东北电力大学 电气工程学院,吉林 吉林 132012;2. 国网河南省电力公司郑州供电公司,河南 郑州 450000;3. 黑龙江省第一水文地质工程地质勘测院,黑龙江 齐齐哈尔161000;4. 国网吉林省电力有限公司电力科学研究院,吉林 长春130021)
SVC与TCSC优化配置在电力系统静态电压稳定中的应用
李娟1,许欣1,李壮1,庄海军2,齐永志3,高松4
(1. 东北电力大学 电气工程学院,吉林 吉林 132012;2. 国网河南省电力公司郑州供电公司,河南 郑州 450000;3. 黑龙江省第一水文地质工程地质勘测院,黑龙江 齐齐哈尔161000;4. 国网吉林省电力有限公司电力科学研究院,吉林 长春130021)
摘要:为提高电力系统静态电压的稳定性,提出将静止无功补偿器(staticvarcompensator,SVC)与可控串联补偿装置(thyristorcontrolledseriescompensator,TCSC)相结合并作用于电力系统线路中,运用动态连续潮流法计算电力系统静态电压稳定裕度的新方法。首先建立SVC与TCSC的稳态模型;然后引入节点参数因子和支路参数因子的概念,运用模态分析法确定系统母线和支路的薄弱点,并联SVC对母线薄弱点进行无功补偿,串联TCSC优化薄弱线路功率分配;最后运用动态连续潮流法求出静态电压稳定裕度。以IEEE-14节点系统进行仿真计算,并对无灵活交流输电(flexibleACtransmissionsystem,FACTS)装置、单独安装SVC或TCSC、SVC和TCSC相结合情况下的系统静态电压稳定裕度值作比较,结果表明所提新方法能够快速、准确地提高电力系统静态电压稳定性。关键词:灵活交流输电;静止无功补偿器;可控串联补偿装置;静态电压稳定裕度;动态连续潮流法;模态分析法
随着全球电力系统规模的不断扩大和负荷的逐渐增多,电压崩溃已成为近代电力系统研究的重要课题[1]。灵活交流输电(flexibleACtransmissionsystem,FACTS)作为新兴的技术,因具有快速灵活的控制能力而越来越受到人们的重视[2]。本文以动态连续潮流法为分析工具,以电力系统静态电压稳定负荷裕度为目标函数,将静止无功补偿器(staticvarcompensator,SVC)与可控串联补偿装置(thyristorcontrolledseriescompensator,TCSC)相结合作用于电力系统,通过功率注入模型将其作用等效为一系列电压和功率的约束,并直接运用于动态连续潮流法中,通过提高静态电压稳定负荷裕度来提高电力系统静态电压的稳定性。
1基本模型
1.1SVC基本模型
1.1.1数学模型
分立式SVC包括可控饱和电抗器、晶闸管投切电容器(thyristorswitchedcapacitor,TSC)、晶闸管控制电抗器/晶闸管投切电抗器(thyristorcontrolledreactor/thyristorswitchedreactor,TCR/TSR),以及它们之间结合起来构成的组合式SVC[3]。
图1为TSC-TCR型SVC的原理结构。为了降低SVC的造价,大多数SVC通过降压变压器并入电网。调整TCR支路晶闸管的触发角,可以平滑地调整其并联在系统中的等值电抗。TSC通过对阀的控制使电容器有两种运行状态:将电容器直接并联在系统中,或将电容器退出运行。为了扩大SVC的调节范围,根据补偿容量的需要,一个SVC可以采用多个TSC支路。
李娟,等:SVC与TCSC优化配置在电力系统静态电压稳定中的应用TCR的基波等效电纳:
式中:α为晶闸管触发延迟角,L为电抗器的电感,ω为系统基波角频率。
SVC的等效电纳
(1)
式中BC为晶闸管投切电容器的电纳。
在实际应用中,为了降低SVC对系统的谐波污染,SVC中还应装设滤波器。对基波而言,滤波器呈容性,即向系统注入无功功率。滤波器在工频下等效为容抗,而在特定频段内表现为低阻抗,从而对谐波分量起到滤波的作用。
1.1.2功率注入模型
在电力系统静态稳定性分析中,SVC可以看成一个并联于系统的可变电纳,在一定的范围内,能以一定的响应速度跟踪输入的电纳参考值,使SVC发出或吸收无功功率,其电纳值由SVC的控制器决定。SVC接入系统的功率注入模型如图2所示。
SVC向母线节点i注入的无功功率
(2)
式中:Ui为母线节点i的电压,C为TSC中并联电容器的电容。从式(1)、式(2)可以看出,SVC的等效电纳和注入系统的无功功率都是关于晶闸管延迟角α的连续函数。SVC通过控制α来连续改变等效电纳,进而改变SVC输出的无功功率,起到调节母线电压的作用。
1.2TCSC基本模型
1.2.1数学模型
TCSC是由一系列电容器串联组成的,每个电容器都并联一个适当容量的晶闸管阀旁路,后者包括一组反并联的晶闸管。TCSC可以快速、连续地改变所补偿线路的等值电抗,因而在一定的运行范围内,可以将线路的输送功率控制为所期望的数值。由于TCSC具有反应速度快、操作灵活方便的特点,通过对晶闸管阀触发角的控制,使得输电系统线路的阻抗值动态可调,从而达到平滑调节串联补偿电容器容抗值的目的,并且灵活调节输电线路补偿度,改善系统静态电压稳定性[4]。图3为TCSC的原理结构。
TCSC稳态运行时,其等效基波电抗XTCSC与触发角α的关系为
其中
式中:XC为电容器的基波容抗,XL为α=90°时TCR的等效基波感抗。一般XC/XL=3.3~10.0,这样当触发角在90°~180°之间变化时,可确保出现唯一的感性、容性区。
当α=90°时,TCR的阻抗取得最小值XL,由于XL 1.2.2功率注入模型 等效功率注入模型实质是将TCSC对系统的影响转移并迭加到其所在支路的两端节点上,TCSC可以看作是串联在系统中的一个可变的电抗,用等效附加注入功率对TCSC作虚拟等效,故可以看作原始网络的节点导纳矩阵还保持对称性,方便对加入的TCSC作处理,即可以利用传统潮流计算中雅克比矩阵的迭代求解原理来进行潮流求解,同时还验证TCSC对电力系统网络的影响。其等效模型如图4所示。 TCSC向系统节点j注入的有功功率和无功功率分别为: (3) (4) 式中:Uj、Uk分别为母线节点j、k的电压,δj、δk分别为母线节点j、k的电压相位。 TCSC向系统节点k注入的有功功率和无功功率分别为: (5) (6) 从式(3)—(6)可以看出:通过控制α来连续改变TCSC的等效电抗,进而调节线路有功功率和无功功率的分配,优化薄弱线路的潮流分布。 2SVC与TCSC安装位置确定方法 2.1模态分析法 采用FACTS装置提高系统电压稳定性,必须选取最佳安装点。对于实际电力系统,通过每条线路的模拟仿真来确定安装位置是不现实的,而模态分析法是在雅克比矩阵的特性域内对灵敏度法作更为深入的处理,更符合系统的真实运行情况[5-7]。本文充分考虑系统实际运行情况,引入节点参与因子和支路参与因子的概念,通过计算确定系统薄弱的区域,作为SVC与TCSC的最佳安装点。 模态分析法的分析过程为:首先,利用降阶雅克比矩阵的特征值确定系统是否处于稳定状态,当所求取的特征值出现负值时即认为系统处于失稳状态;其次,依据降阶雅克比矩阵特征值求取每一个特征值所对应的一对特征向量,进而推导和确定相应参数值的参与因子,确定其对系统模态的影响程度,通过计算给出系统的薄弱区域或者节点,以确定FACTS装置最佳安装点。 设系统极坐标潮流方程式为: (7) 式中:ΔPi、ΔQi分别为注入节点i的有功功率、无功功率的不平衡量,PGi、QGi分别为发电机在节点i发出的有功功率、无功功率,PLi、QLi分别为负荷在节点i消耗的有功功率、无功功率,Gij、Bij分别为节点i、j之间的导纳实部和虚部,δij为母线节点i、j的电压相位差。 当把负荷所吸收的功率及发电机的出力看作常数时,由式(7)得到修正方程为 式中:ΔP、ΔQ、ΔU、Δδ分别为节点注入有功功率不平衡量、节点注入无功功率不平衡量、节点电压不平衡量、节点电压相位不平衡量,JPU、JQU、JPδ、JQδ分别为有功功率对电压的偏导数、无功功率对电压的偏导数、有功功率对电压相位的偏导数、无功功率对电压相位的偏导数。 令ΔP=0,得 式中JR为系统降阶雅克比矩阵。 根据模态分析法的基本原理,需要求取JR的特征值与特征向量。对JR进行特征值分解,可得 式中η、ξ、Λ分别为JR的左特征向量矩阵、右特征向量矩阵、特征值矩阵。 整理得 设ΔUm为模态电压变化量,ΔQm为模态无功功率变化量,令ΔUm=ηΔU,ΔQm=ηΔQ,得 对于第i个母线节点,其模态电压变化量ΔUmi与模态无功功率变化量ΔQmi有如下关系: 式中γi为ΔQmi对ΔUmi的影响因子。 节点j的电压-无功功率灵敏度可表示为 (8) 式中:ΔUj、ΔQj分别为节点j模态电压变化量、模态无功功率变化量,ξji为右特征向量第j行第i个元素,ηij为左特征向量第j列第i个元素。 由式(8)可以看出:电压-无功功率灵敏度并不识别单个模态的信息,仅反映系统模态的综合效应信息。 为找出系统薄弱区域,定义母线参与因子βbus(ij)=ξijηij,其值越大,表明γi在母线j对电压-无功功率灵敏度的影响越大。母线参与因子较大的线路往往是系统的重负荷区或者薄弱环节,这也就确定了系统的薄弱区域或者关键节点,在薄弱母线节点上并联安装SVC,通过无功补偿的方式来提高薄弱母线节点电压的稳定性。 定义支路j-k的参与因子 式中:ΔPloss(jk)为支路j-k有功功率损耗,ΔPloss为网损变化量。如果βbranch(jk)较大,表示该支路为弱连接或重负荷,为系统薄弱区域或关键支路,在薄弱支路上串联安装TCSC,通过功率补偿来调节薄弱支路的功率分配。 3求取静态电压稳定裕度 静态电压稳定裕度是指从当前运行点出发,不断增加系统负荷直至发生电压崩溃,从崩溃点到当前运行点的距离[8]。优化目标是通过调节发电机端电压、变压器分接头位置、FACTS装置及投切电容器的无功补偿容量等控制变量来求出静态电压稳定裕度,在计算过程中,不平衡功率由负荷变化量λ和网损变化量ΔPloss两部分组成。常规连续潮流中,网损部分由选定的平衡节点单独承担,但网损增量较大时选择不同的平衡节点将导致分析计算结果不同,甚至相差较大[9]。因此,本文运用动态连续潮流法计算静态电压稳定裕度,建立动态潮流模型,结合功率-频率静特性系数与发电机转子加速的影响进行不平衡功率分配。 3.1动态连续潮流数学模型 在动态连续潮流中,系统的负荷增量λ和网损增量ΔPloss根据不平衡功率的分配系数进行分配。 电力系统网络的有功总损耗 式中x为系统的静态状态向量(即节点电压振幅和相位)。 系统中的不平衡功率 式中:Ploss(x0)为基态时系统的网损值,x0为系统的基态静态状态向量。 动态连续潮流数学模型的极坐标形式为: 其中: 式中:PG0i、QG0i分别为基态时发电机节点i发出的有功功率和无功功率;PL0i、QL0i分别为基态时负荷节点i消耗的有功功率和无功功率;KPL、KQL分别为各负荷节点的有功功率增长系数和无功功率增长系数,一般取恒功率因数的增长方式;ai、bi分别为发电机节点与负荷节点的单位调节系数;ci为发电机根据转子转动惯量分担不平衡功率的系数;KGi为发电机节点i参与一次调频的功率-频率静特性系数;KLi为负荷节点i参与一次调频的功率-频率静特性系数;Kt为时间常数;TJi为发电机节点i的系统惯性时间常数;Si、Pi分别为发电机节点i的视在功率和有功功率。 由表征功率-频率静特性变化的运动方程得到频率偏移量 可见,在静态电压稳定裕度计算过程中,也可以对系统的频率进行监视。 动态连续潮流法中的不等式约束有状态变量约束和控制变量约束。状态变量的不等式约束为: 控制变量的不等式约束为: 3.2计及SVC与TCSC的动态连续潮流数学模型 在等效附加注入功率理论的基础上,结合前文所述的动态连续潮流模型,直接将SVC与TCSC等效注入功率模型带入动态连续潮流中,建立可用于静态电压稳定裕度计算的潮流计算数学模型。潮流计算数学模型为: (9) 式中:ΔP(inj)、ΔQ(inj)分别为FACTS元件在其安装节点及线路的等效附加注入有功功率和无功功率,当系统没安装FACTS元件时,ΔP(inj)、ΔQ(inj)为零。 动态连续潮流与连续潮流的未知数个数相同,平衡点有功方程并不需要参与迭代计算,其求解过程与连续潮流相似,不同的是由于网损增量的引入、不平衡功率分担系数的改变,需要对连续潮流中有功方程和静态状态变量的偏导数进行修正。本文采用直接调整有功失配量法,即把第i-1步的网损增量看作是第i步的网损增量。 在迭代过程中,忽略网损增量ΔPloss(x)的影响,直接利用原雅克比矩阵的稀疏性进行迭代求解,可得到方程(9)的精确解。 4算例分析 本文利用IEEE-14节点系统(如图5所示)对选址、静态电压稳定裕度求取方法进行验证。取节点1为平衡节点,节点2、3、6、8为电压控制节点,节点4、5、7、9、10、11、12、13、14为负荷节点,节点9只用于安装并联电容器,可调变压器位于4-7、4-9、5-6这3条支路。 采用牛顿-拉夫逊法进行一次系统潮流计算,运用模态分析法求出母线节点的母线参与因子值与支路参与因子值,并根据其数值找出系统的薄弱母线节点与薄弱线路。表1、表2分别列出了母线参与因子值和支路参与因子值。 表1母线参与因子值 根据表1,负荷节点4的母线参与因子最大,因此SVC的最佳安装点为母线节点4。根据表2,支路2-4的支路参与因子最大,因此TCSC的最佳安装点为支路2-4。 为了验证本文方法的正确性和可行性,在同样的系统、相同的初始条件下,进行了安装FACTS元件前后的潮流解比较,结果见表3。 由表4可以发现,将TCSC加在线路2-4上不仅可以有效地减小流过支路2-4、1-2上的有功功率, 表3安装FACTS元件前后IEEE-14节点系统支路功率 并且能够增加流过支路5-6上的有功功率,优化线路功率分布,提高电力系统静态电压稳定性。 确定安装位置后,通过动态潮流计算得出静态电压稳定裕度:无FACTS时为1.419 6,安装SVC后为1.543 9,安装TCSC后为1.619 0,安装SVC和TCSC为1.655 2。由此可以明显看出:无FACTS装置时负荷裕度值最小;安装SVC或TCSC装置均能提高系统的静态电压稳定性;并联SVC及串联TCSC装置进行功率补偿时,所求负荷裕度值最大,效果最明显。 5结论 本文提出一种提高静态电压稳定裕度的新方法,即通过同时安装并联型SVC和串联型TCSC装置来提高电力系统静态电压稳定。得出如下结论: a) 并不是在任何支路安装FACTS装置都能提高输电能力。 b) 合理选择安装位置可以使电力系统静态电压稳定裕度提升。 c)FACTS装置的最佳安装数量,以及同时安装SVC与TCSC是否会交互影响,进而制约负荷裕度的最大值,是进一步研究的问题。 参考文献: [1] 薄明明,安亮.动态连续潮流与改进粒子群优化算法相结合的静态电压稳定分析[J]. 黑龙江电力,2013,35(1):62-66. BOMingming,ANLiang.AnalysisofStaticVoltageStabilityBasedontheCombinationofDynamicContinuationPowerFlowandImprovedParticleSwarmOptimizationAlgorithm[J].HeilongjiangElectricPower,2013,35(1):62-66. [2] 汤新光.用FACTS技术提高电力系统静态负荷裕度能力[J]. 江苏电机工程,2006,25(5):38-41. TANGXinguang.ImprovementofthePowerSystemStaticLoadMarginUsingFACTSTechnology[J].JiangsuElectricalEngineering,2006,25(5):38-41. [3] 张靖,程时杰.通过选择SVC安装地点提高静态电压稳定性的新方法[J]. 中国电机工程学报,2007,27(34):7-11. ZHANGJing,CHENGShijie.ANovelSteady-stateVoltageStabilityEnhancementMethodBasedonSVCAllocation[J].ProceedingsoftheCSEE,2007,27(34):7-11. [4] 张健,冀瑞芳.TCSC优化配置提高可用输电能力的研究[J]. 电力系统保护与控制,2012,40(1):23-28. ZHANGJian,JIRuifang.StudyofEnhancementofAvailableTransferCapabilityUsingTCSCOptimalAllocation[J].PowerSystemProtectionandControl,2012,40(1):23-28. [5] 胡艳梅.交直流混联电力系统静态电压稳定性分析及FACTS优化配置研究[D]. 北京:北京交通大学,2014. [6] 邢巍,都洪基.利用模态分析法确定SVC最佳安装地点[J]. 电测与仪表,2014,51(5):91-95. XINGWei,DUHongji.DeterminationoftheSVCOptimumLocationBasedonModalAnalysisMethod[J].ElectricalMeasurement&Instrumentation,2014,51(5):91-95. [7] 庄海军.利用UPFC进行电力系统网损优化控制[D]. 吉林:东北电力大学,2015. [8] 孙宏斌,李钦.基于动态潮流方程的连续潮流模型与方法[J]. 中国电机工程学报,2011,31(7):77-82. SUNHongbin,LIQin.ContinuationPowerFlowMethodBasedonDynamicPowerFlowEquation[J].ProceedingsoftheCSEE,2011,31(7):77-82. [9] 李娟,刘海龙.动态连续潮流与改进捕鱼算法结合计算静态电压稳定裕度[J]. 华北电力大学学报,2013,40(3):11-16. LIJuan,LIUHailong.ImprovedAlgorithmSimulatingFishingAlongtheSearchWhichCalculatesStaticVoltageStabilityMarginbyDynamicContinuationPowerFlow[J].JournalofNorthChinaElectricPowerUniversity,2013,40(3):11-16. 李娟(1972),女,山东荣成人。教授,工学博士,主要研究方向为电力系统运行控制及FACTS。 许欣(1989),男,吉林四平人。在读硕士研究生,主要研究方向为电力系统静态电压稳定性分析。 李壮(1991),女,吉林吉林人。在读硕士研究生,主要研究方向为电力系统稳定与控制。 (编辑李丽娟) ApplicationofSVCandTCSCOptimalConfigurationinStaticVoltageStabilityofPowerSystem LIJuan1,XUXin1,LIZhuang1,ZHUANGHaijun2,QIYongzhi3,GAOSong4 (1.CollegeofElectricalEngineering,NortheastDianliUniversity,Jilin,Jilin132012,China; 2.ZhengzhouPowerSupplyCompanyofStateGridHenanElectricPowerCompany,Zhengzhou,Henan450000,China; 3.HydrogeologyandEngineeringGeologyExplorationInstituteofHeilongjiangProvince,Qiqihar,Heilongjiang161000,China; 4.StateGridJilinProvinceElectricPowerResearchInstitute,Changchun,Jilin130021,China) Keywords:flexiblealternativecurrenttransmission;staticvarcompensator(SVC);thristorcontrolledseriescompensator(TCSC);staticvoltagestabilitymargin;dynamiccontinuoustrendmethod;modalanalysismethod Abstract:Inordertoimprovestabilityofstaticvoltageofthepowersystem,itisproposedtocombinestaticvarcompensator(SVC)withthyristorcontrolledseriescompensator(TCSC)inpowersystemlinesandusedynamiccontinuoustrendmethodforcalculatingstaticvoltagestabilitymarginofthepowersystem.Firstly,steadystatemodelforSVCandTCSCisconstructed,conceptsofnodeparameterfactorandbranchparameterfactorareintroducedandmodalanalysismethodisusedtodeterminevulnerabilitiesofsystembusbarandbranches.Inaddition,parallelSVCisadoptedforreactivepowercompensationforweakspotsofbusbar,seriesTCSCisusedforoptimizingpowerdistributionofweaklinesanddynamiccontinuoustrendmethodisappliedtoworkoutstaticvoltagestabilitymargin.IEEE-14nodesystemisusedforsimulatingcalculation,andstaticvoltagestabilitymarginvaluesofdevicewithoutflexiblealternativecurrenttransmissionsystem(FACTS),singleinstallationofSVCorTCSC,combinedinstallationofSVCandTCSCarecompared.Resultsindicatetheproposednewmethodisabletoquicklyandcorrectlyimprovestaticvoltagestabilityofthepowersystem. doi:10.3969/j.issn.1007-290X.2016.04.012 收稿日期:2015-10-23 中图分类号:TM712.2 文献标志码:B 文章编号:1007-290X(2016)04-0067-06 作者简介: