例举数列极限的若干种不同求法

李玉萍　张金诺（.郑州师范学院数学与统计学院，河南郑州　450044；.中国地质大学经济管理学院，湖北武汉　430074）



例举数列极限的若干种不同求法

李玉萍1张金诺2
（1.郑州师范学院数学与统计学院，河南郑州450044；2.中国地质大学经济管理学院，湖北武汉430074）

【摘 要】极限是高等数学教学中的重要环节，也是贯穿整个微积分教学的主线。本文简单地介绍了计算极限的几种方法，讨论了如何利用数列极限的定义、两边夹法则、单调有界定理、致密性定理、柯西收敛准则、数列的四则运算法则、两个重要极限法、Stolz定理法、定积分定义法、级数性质法、拆项法与错位法来计算数列的极限。

【关键词】两边夹法则单调有界定理致密性定理柯西收敛准则Stolz定理

极限是高等数学教学中的重要环节，也是贯穿整个微积分教学的主线。它描述了变量的变化趋势，是从有限到无限、从量变到质变、从近似到精确必不可少的推理工具。极限是分析学的基础，极限问题是分析学中的困难问题之一。极限问题的基本思想对解决分析学中面临的问题自始至终起关键作用，有关一元、二元、多元微积分学和级数等概念及一些基本的思想都是利用极限的思想而提出来的。而数列极限又是极限的基础，是整个数学分析中极限部分的重要内容，下面从以下几个方面来谈谈数列极限的几种求法

1　关于数列极限四种最常见的求法

1.1定义法

1.2两边夹法则

显然，这个和是无穷限项的，不能用极限的运算法则来求极限，求此和也不是一件容易的事情，我们可以利用数列的特性。

所以根据数列极限的两边夹法则可得

1.3四则运算法则

此方法是利用一些数列其已知的极限来求这些数列经过四则运算后形成的数列的极限，这样就有相当一些数列极限不必再用ε-N定义求极限，而简便地使用四则运算法则来求极限。

1.4两个重要极限

利用重要公式来求极限或者是转化为函数的极限，这种方法必须得在牢记住重要极限的形式和它的值的基础上，并且对所求的式子作适当的变形，从而来达到可以求出其极限的目的，这种方法应用比较灵活，其有相当强的技巧性。

2　其他几种求数列极限的方法

2.1Stolz定理法

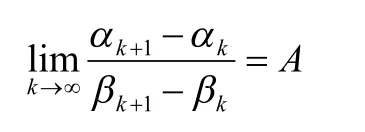
证明：利用Stolz定理

2.2定积分定义法

这种方法主要用于求和式的极限，极为方便。

例如

可以把它看成是函数xarctanx 在区间［0，1］上的积分和，它所运用的是把区间［0，1］平均分成等份，并且均取每个均匀的小区间的右端的函数值，可得

2.3级数性质法

级数实质上是一个无穷序列的和的形式，而它的部分和其实就是一个数列。有的时候为了方便，可以将数列极限看成是某个级数的部分和，这样便可以更方便、更快速、更简洁的求出原数列的极限。

2.4错位法与拆项法

以上主要针对数列极限的几种求法进行了初步的探索，要想求出一些数列的极限而在题目中没有说明极限存在的条件下，我们需要先判别该数列的极限是否存在，然后进而求之，在上文中我们介绍了几种如何判别数列极限存在的方法，在对数列极限进行求解的时候，往往不是一个过程就能解决的，通常需要多种方法的结合。不同类型的数列极限问题，需要用不同的方法解决，我们在学习数列极限的过程中，只有不断的进行总结、不断的完善知识理论和结构，才能够对相应的题目对症下药、有所创新和突破，所以我们应该在学习的过程中，由浅入深地逐步理解和掌握。

参考文献：

［1］华东师范大学数学系.数学分析（上册，第四版）［M］.高等教育出版社，2011.

［2］郑允利《求数列极限的方法探讨》［J］高等函数学报（自然科学版），2010年06期.

［3］罗威.如何用数列极限定义证明数列极限问题［J］.沈阳大学学报，2004，16（4）:85-86.

［4］淮乃存.利用定积分定义求数列极限［J］.陕西师范大学学报:自科版，2003，31（S1）:30-35.

［5］裴礼文.数学分析中的典型问题与方法［M］.北京:高等教育出版社，2006（2）:57-64.

基金项目：河南省教育厅课程改革研究项目 （2016-JSJYZD-072）。

作者简介：李玉萍（1971—），河南荥阳人，副教授，硕士，研究方向为数学教学论。