一种电网规划方案决策的灵敏度分析算法

司怀伟　王清心　丁家满

摘 要： 方案决策中的不确定因素越来越多，对决策结果在不确定环境下的灵敏度分析显得尤为重要。传统灵敏度分析方法常常忽略不确定性或只是简单平均将导致规划方案决策的偏差甚至错误。针对上述问题，提出一种基于概率盒理论的削减分析算法，首先对不确定性变量进行概率盒建模，其次将各指标概率盒输入决策方程计算并得到决策基数，然后依据决策基数对方案中各指标逐一消减，并计算得到其灵敏度。最后将该方法应用于电网规划方案决策中，实验结果表明该方法具有较强的实用性。

关键词： 灵敏度分析； 概率盒； 不确定性分析； 削减法

中图分类号： TN911?34； TP301.6 文献标识码： A 文章编号： 1004?373X（2016）07?0149?05

Abstract： The more uncertainty factors in the scheme decision are particularly important to the sensitivity analysis of the decision results in the uncertain environment. The traditional sensitivity analysis methods often ignore the uncertainty or simply average the deviation error， which results in the deviation of the planning decision or even mistake. For the above problems， a cutting analysis algorithm based on the probability box theory is proposed. The probability box of the uncertainty variables is modeled， and the input decision?making equation of each indicator probability box is calculated to obtain the decision cardinal number， then each indicator in the scheme is orderly cut according to the decision cardinal number to obtain its sensitivity. The method was applied to the decision?making of the power grid planning scheme. The experimental results show this method has strong practicability

Keywords： sensitivity analysis； probability box； uncertainty analysis； cutting method

0 引 言

决策方案中不确定性因素出现的越来越多，不确定性指标的处理与分析显得尤为重要[1]。灵敏度分析是不确定因素环境中多属性决策的必要补充[2]，通过灵敏度分析可以较好地识别出关键指标[3]。灵敏度分析是一种根据参数的输入研究输出结果变化的不确定性分析[4]。如果输入参数变化很小，引起输出结果的变化很大，则认为该参数是灵敏的。由此可见，决策方案中某项指标发生变化却忽略该变化，则会造成一定的损失，所以有必要对规划方案进行灵敏度分析来规避方案中可能出现的风险。

许多研究者逐渐发现灵敏度分析的重要性，并且出现许多经典分析方法，如非参数方法[5]、方差分析法[6]以及矩独立分析方法[7]。上述方法大都是对数据进行分析，然后代入模型，代入的方式包括区间范围或者是一个平均数，但是大多数方法都忽略了数据的一些概率特性，进而影响灵敏度分析的结果[8]。在有不确定性指标先验概率的情况下，贝叶斯灵敏度分析是一种很好的灵敏度分析方法[9]，但是在先验概率未知情况下可用性变小。

针对上述问题，本文基于文献[8，10]提出一种概率盒的方法处理数据，该方法通过累计概率分布的方法对不确定性指标进行建模，可以很好地找到不确定性指标的变化范围。然后通过卷积和控制变量的削减方法进行灵敏度分析。概率盒方法在美国圣地安娜实验室核工程方面取得了巨大成就，并且在股票预测方面也取得了一定进展[1，8，10]。

1 概率盒及其相关理论

1.1 证据结构体

传统的概率表示法是一个点，而证据论指出这些点是由观测或测量得出的，而这些观测和测量往往不精确，这些数据有很大的不确定性，甚至有许多数据是不可测量的。证据结构体则用一组在这个点周围的实数集合来定义这个点的概率，这些实数集合称为焦元。一个概率分布函数往往是一条实数线，用证据结构体表示概率的方法则不是实线上的点而是焦元。

1.2 概率盒理论

不确定性分析是把不同变量代入数学模型中作为输入，分析其输出结果的变化。代入通常分为两种：一种是输入值附近可能的区间范围；另一种是输入变量可能的概率分布。在一个确定的计算中，当模型中存在计算所使用的变量是不确定的情况时，可以利用区间范围进行不确定性分析。采用Monte Carlo模拟法可以模拟出变量出现的概率，产生的概率分布表示不确定性变量可能值的点估计。目前许多灵敏度分析方法是构建一个概率计算的概率不确定性分析，其结果是一个二阶概率估计，然而计算十分繁琐，并且得到的可视化结果难以理解，这样的研究很难进行；或者，将边界参数应用于概率计算和到达区间范围的概率分布，即“概率界限分析（PBA）”。这种方式表示不确定性概率分布的累积分布函数完全处于一对边界分布函数之间，即为“概率盒（P?box）”。概率盒之所以可以进行不确定性概率边界分析，是因为它定义了概率分布周边的分布情况，以及不确定性输入或输出变量的分布，这种分析通过对不确定性分布函数的周围进行边界划分，保证产生的界限将完全处在累积分布函数之间。概率盒的边界分布包含所有在该终端取值相同的概率分布。

1.3 DS结构体和概率盒的关系

DS结构体是一种不精确的分布，一个焦点元素代表一组可能[x]概率值，现有的证据论和方法区分不出来可能的[x]值。这种焦元概率值的不可区分性使证据论具有局限性。而P?box用概率界限的方法可以解决概率不确定性问题，根据不确定点[z]的基本概率事件可以做出一条关于[z]的概率实线[g（z）。]此方法主要考虑不确定性问题的概率范围，而不是[x]值，所以概率盒用一个概率区间表示一个不确定点的概率[11]。二者关系不是一对一的关系，可能是几个DS结构体组成一个P?box。因此， DS结构体不是一个信息保存操作。二者结合对于风险分析是一个不错的应用。

1.4 得到概率盒的方法

得到概率盒的方法有许多，本文主要采用直接估计法又称专家估计。该方法的基本思想是根据已经掌握的概率分布或者专家的经验得到某一不确定变量概率分布。这种分析是在已有的不确定性分析上进行进一步推断。当不确定性变量信息足够时概率盒的上、下界将退化成累计分布函数。在某些情况下，由于知识的局限性，一个分布的参数是不确定的，只能估计出参数的一个大致区间，此时可以直接计算出概率盒的边界。例如一个均匀分布的两个参数分别在[a，b]和[c，d]之间，这种分布可以累积成一对分布函数把这种分布的所有情况包括进去。概率盒的左边界是一个在[a]和[c]之间的累计均匀分布。可以用均匀分布[[a，c]]来表示，同样右边界用均匀分布[[b，d]]表示。对于大多数已知的分布函数可以用这种方法进行累计求出概率盒的左右边界。概率盒的左边界是在[a]和[c]之间均匀分布的累积函数。其中[a]表示均值，[c]表示方差。

这是得到概率盒方法中最简单、最基本的一种方法。得到概率盒的方法还有建模、贝叶斯概率建模等方法，特别说明一下贝叶斯也是一种很好的不确定性分析方法，但是其必须知道先验概率，否则就无能为力了。得到概率盒方法步骤如下：

（1） 不确定数据采集，根据数据的大致特征和数据量进行不确定建模分类。

（2） 根据数据大致类型进行建模，若符合直接估计建模，计算所需要参数的范围，如均匀分布的均值和方差。

（3） 进行分布函数的累积，得到概率盒的上、下界。

（4） 根据累积分布后的函数画出概率盒的示意图。

（5） 进行不确定性分析，特征提取等操作。

2 基于概率盒的不确定性灵敏度算法

数据量不断增大，数据的不确定性也越来越大，主要有偶然不确定性和主观不确定性。偶然不确定性是指数据本身的变化，主观不确定性是由于人们掌握的数据、认识数据的方法工具不全面造成的。传统的做法是把不确定数用一个精确的数，或者用一个概率区间代替，模拟不确定数的变化。随着计算机的发展，蒙特卡罗二阶概率把变量的二阶概率通过大量反复的重复模拟后，形成一个概率，并将该概率代入不确定分析方法中。但计算量是巨大的，产生的结果也难以让人理解。

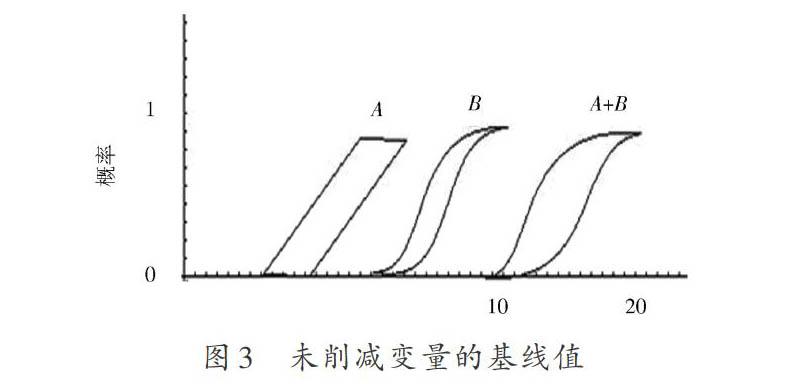
基于概率盒的灵敏度分析方法充分考虑了偶然不确定性和主观不确定性，在变量替换的灵敏度分析方法中不仅可以控制变量的不确定性，还可以控制变量之间的依赖关系。如图3展示了一个简单的变量控制的灵敏度分析法。图3描绘了[A]和[B]是两个不确定的数字，在基线的情况下对其中的削减进行比较，如图4，图5所示。不确定数[A]被指定为一个均匀的分布，其最小值介于4～5之间，最大值为5～6之间。不确定变量[B]被指定为正态分布方差的均值是8～9之间的值。它的两个端点值被任意截断为5.4和11.6。

控制不确定性变量[A，]令它的不确定性慢慢地变化如图4，然后卷积得到模型的输出影响大约为47%。

同理，对变量[B]进行控制其变量的不确定性，如图5所示。模型的输出结果影响是47.2%。将本方法与传统的灵敏度分析方法对比，方差分析中[A]和[B]的方差相差很大对结果的影响也是方差较大的[B]对模型输出结果影响较大。而概率盒的灵敏度分析法结果显示[A]和[B]对结果的影响都仅在47%左右。

由以上分析可知，基于概率盒的削减算法步骤如下：

（1） 对数据进行简单的统计，做简单的数字特征提取，如建立简单的坐标轴观察数据的形状，均值方差求值。

（2） 根据步骤（1）中的简单统计选择相应的概率盒建模方法。

① 数据分组；

② 数据分组后的均值方差求值；

③ 对均值方差进行累计求分布。

（3） 重复步骤（1）和步骤（2）操作对所有变量进行概率盒建模。

（4） 控制变量的不确定性与其他变量畸形卷积。

（5） 重复步骤（4）直到每一个变量都进行过控制。

3 实验结果及分析

概率盒针对不确定性指标的分析有很大的优势。在电网规划中存在着大量的不确定性信息，以某省输电网“十二五”规划方案决策为实例，说明概率盒在电网规划方案决策的概率灵敏度分析方法的优势。

4 结 论

本文采用概率盒和削减方法对不确定数据进行灵敏度分析，并以电网规划方案灵敏度分析为例，证明了该方法的有效性。通过对不确定数据的灵敏度分析，有助于决策者识别关键指标，规避风险。

尽管概率盒方法有许多优点，但是国内发展尚不完善，研究资料很少。本文也只是对概率盒的初步应用，将概率盒的其他优点应用于灵敏度分析中是下一步的研究方向。

注：本文通讯作者为王清心。

参考文献

[1] TUCKER W T， FERSON S. Sensitivity in risk analyses with uncertain numbers [R]. New York： [s.n.]， 2006.

[2] 林振智，文福拴，薛禹胜.黑启动决策中指标值和指标权重的灵敏度分析[J].电力系统自动化，2009，33（9）：20?25.

[3] 陈光，林振智，周浩，等.电网规划方案决策的概率灵敏度分析[J].电力系统自动化，2013（9）：41?46.

[4] LASKEY K B. Sensitivity analysis for probability assessments in Bayesian networks [J]. IEEE transactions on systems man and cybernetics， 1995， 25（6）： 90l?909.

[5] SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates [J]. Mathematics and computer simulation， 2001， 55（13）： 221?280.

[6] KIUREGHIAN A D. Analysis of structural reliability under parameter uncertainties [J]. Probabilistic engineering mechanics， 2008， 23（4）： 351?358.

[7] BOREONOVO E. A new uncertainty importance measure [J]. Reliability engineering and system safety， 2007， 92（6）： 771?784.

[8] FERSON S， KREINOVICH V， GINZBURG L， et al. Constructing probability boxes and Dempster?Shafer structures [J]. Other information， 2003（4）： 171?173.

[9] 姚宏亮，张一鸣，李俊照.动态贝叶斯网络的灵敏性分析研究[J].计算机研究与发展，2014（3）：536?547.

[10] FERSON S， HAJAGOS J， BERLEANT D， et al. Dependence in Dempster?Shafer theory and probability bounds analysis [J]. Managing hedge fund managers quantitative and performance measures， 2004， 47（2）： 134?135.

[11] DING Jiaman， DU Yi， WANG Qingxin， et al. P?box theory and SVM methods with application in pattern recognition [J]. Applied mechanics and materials， 2014（4）： 651?653.

[12] 陈超.电力大数据质量评价模型及动态探查技术研究[J].现代电子技术，2014，37（4）：153?155.

[13] 任博，吕震宙，王攀，等.分布参数不确定情况下全局灵敏度及高效求解方法[J].西北工业大学学报，2013（4）： 540?546.

[14] 孙强，岳继光.基于不确定性的故障预测方法综述[J].控制与决策，2014（5）：769?778.