二维转台的模态分析与试验验证

贺 帅，王忠素

（中国科学院长春光学精密机械与物理研究所，长春 130033）



二维转台的模态分析与试验验证

贺 帅，王忠素

（中国科学院长春光学精密机械与物理研究所，长春 130033）

摘 要：国内对于二维转台的有限元仿真并不少见，但将仿真结果与试验结果进行比较的研究却很少，为此开展了对二维转台的仿真结果进行试验验证的工作。以某二维转台为研究对象，首先介绍了二维转台的结构形式并对其中的轴承连接进行了模型等效；接着对二维转台进行了有限元建模并重点介绍了轴承的MPC建模方式；然后通过简支梁模型对MPC模拟轴承的铰支座特性进行了理论验证；最后对二维转台进行了仿真分析与试验验证。仿真与试验结果表明：MPC模拟的简支梁在其端部绕着轴承外圈发生了转动，MPC模拟了简支梁的转动特性；MPC模拟的简支梁中点位移与材料力学计算的中点位移误差在4.1%，说明MPC能比较准确的模拟铰链特性；二维转台在x、y、z三个方向计算的固有频率与试验结果误差在8%，说明MPC能较准确的模拟了轴承，适合二维转台的模拟。

关键词：二维转台；轴承；铰支座；MPC；有限元；简支梁；模态分析；特征试验

0　引言

二维转台广泛应用于航天、航空等高科技领域，如美国的天基侦查系统［1，2］、我国风云三号卫星上搭载的太阳辐射监测仪［3］以及嫦娥三号着陆器上搭载的极紫外相机［4］等。用于航天领域的二维转台在火箭发射过程中要经受严酷的力学环境（正弦振动、随机振动与冲击等），需要结构具有足够的刚度。航天产品的研发费用昂贵，在实际产品投产前需要对其进行有限元分析。有限元分析的好坏直接影响了航天产品的研发成本与周期，因此如何有效的模拟二维转台尤为重要。

二维转动的主要非线性环节是轴承连接。轴承的有限元模拟方面有接触模拟、Gap模拟［5］与MPC（Multipoint constraints）模拟。接触与Gap模拟属于非线性模拟，一般适用于小规模的有限元分析中。而二维转台零部件较多，有限元网格数量较多，接触模拟与Gap模拟很难用于实际工程中，因此实际工程中往往采用MPC模拟二维转台的转动。国内对于二维转台的有限元仿真并不少见，但将仿真结果与试验结果进行比较的研究却很少，为此本文采用目前流行的MPC模拟轴承的方法对某二维转台进行有限元建模与分析，并对仿真结果进行试验验证。

本文首先介绍二维转台的结构形式并分析了二维转台中轴承的等效形式，接着介绍了二维转台中各活动部件的建模方法，特别是轴承的建模，最后对二维转台进行了仿真分析与试验验证。

1　二维转台机构

二维转台主要包括方位轴及其驱动组件、俯仰轴及其驱动组件、U形架与成像单元等，二维转台三维模型如图1所示。

图1　二维转台三维模型图

成像单元由俯仰轴两端的轴承承担。俯仰轴一端轴承为一对角接触球轴承，采用压圈压紧轴承内外圈，同时承受径向和2个方向的轴向负载，可以等效为固定铰支座；另一端为深沟球轴承，主要承受径向负荷，轴向可以少量位移，以补偿温度变化带来的影响，可以等效为活动铰支座。方位轴也是采用一对角接触球轴承来承担双向轴向与径向负载，因此可以等效为固定铰支撑。

2　有限元建模

二维转台有限元模型如图2所示。

图2　二维转台有限元模型

2.1轴承模拟

采用MPC模拟轴承的有限元模型如图3所示。其中节点1通过MPC（约束6个自由度）与轴承外圈相连，节点2通过MPC（约束6个自由度）与轴承内圈相连，节点1与节点2之间采用MPC相连（模拟固定铰支座轴承的节点1与节点2之间的MPC约束ux、uy、uz三个自由度，释放rx、ry、rz三个自由度；模拟活动铰支座轴承的节点1与节点2之间的mpc约束ux、uy两个自由度，释放uz、rx、ry、uz的自由度）。MPC模拟的轴承的轴向刚度与径向刚度无线大，这种模拟方式可以用在轴承的刚度远大于轴系其他位置刚度时的模拟。

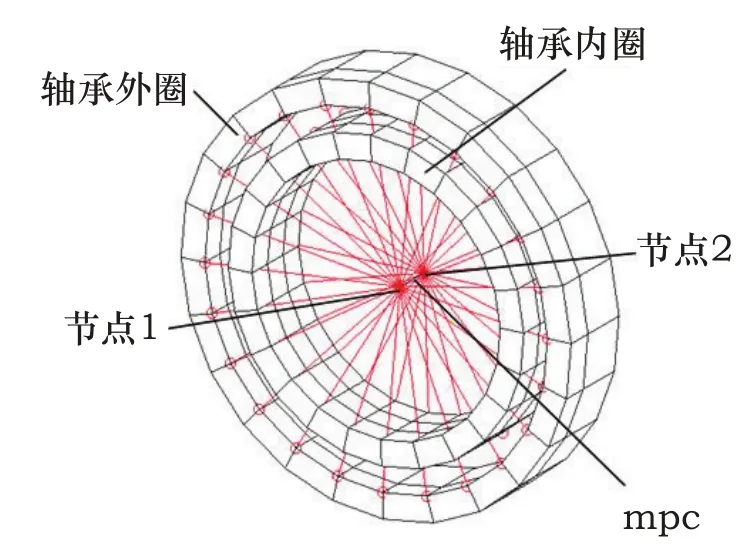
图3　轴承有限元模拟

2.2制动器锁紧模拟

二维转台在发射时需要通过制动器锁紧，制动器的动子部分与转动轴系相连，制动器的定子部分与轴系的定子相连。二维转台的制动器属于摩擦型的，带电自锁时制动器动子与定子通过端面压紧自锁，当自锁力比较大时可以假定定子与动子部分是一个整体，有限元模拟时在制动器定子与动子接触面处节点耦合处理。

2.3电机与编码器模拟

电机与编码器分为定子部分与转子部分，有限元处理时电机与编码器的定子部分与二维转台的定子部分相连，转子部分与转子部分相连。

3　仿真分析与试验验证

3.1轴承仿真

由第1章可知，轴承可以等效为固定铰支座或活动铰支座，采用第2.1节介绍的方法可以模拟轴承的铰接，本文采用了如图4所示的简支梁对MPC模拟铰支座的方法进行了验证。简支梁为空心梁，其主要参数如表1所示。

图4　简支梁简图

表1　简支梁主要参数

简支梁有限元模型如图5所示，轴承是能绕回转轴自由转动的，有限元计算时不允许存在刚度自由度，因此约束了轴承绕回转轴的自由度（rz），其对简支梁分析结果无影响，在后面分析的二维转台中轴系的转动由制动器锁定，MPC模拟的轴承需要释放其转动自由度。

图5　简支梁有限元模型

由材料力学的知识可知，简支梁中点位移为：

有限元与材料力学分析的简支梁中点位移如表2所示，简支梁变形云图如图6所示。

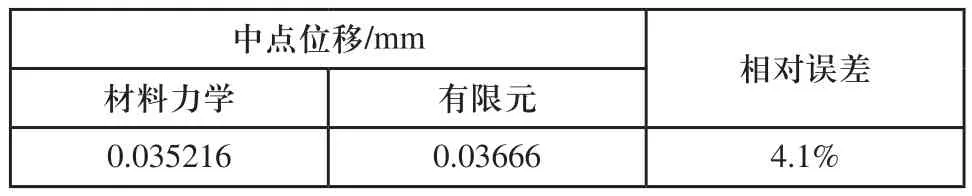
表2　简支梁中点位移

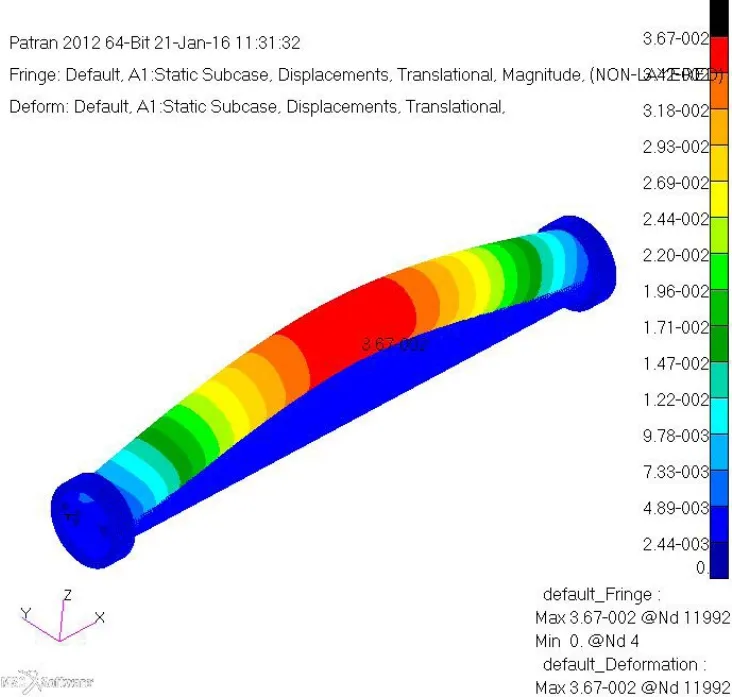
图6　简支梁变形云图

由图6可知，简支梁在端部相对轴承外圈发生了转动，MPC模拟了铰支座的转动特性；由表2可知，MPC模拟的简支梁的中点位移与材料力学计算结果很接近，MPC能比较准确的模拟铰链特性。

3.2二维转台模态分析

将2.1节中轴承的建模方法用在二维转台轴承的建模中，二维转台在x、y、z方向的固有频率及振型如表3所示。由表3可知x向振型是整机在x向的振动，影响该阶固有频率的主要因素是轴系、轴承等在x向的刚度；y、z振型是绕轴系的转动，影响该阶固有频率大小的主要因素是轴系锁紧后的扭转刚度。

表3　二维转台固有频率

图7　二维转台振型图

3.3二维转台试验验证

为了获取二维转台的固有频率，采用与实际结构1：1的初样件进行了三个方向的0.2g特征试验。试验现场照片如图8所示。z向特征试验曲线如图9所示。

图8　二维转台试验现场照片

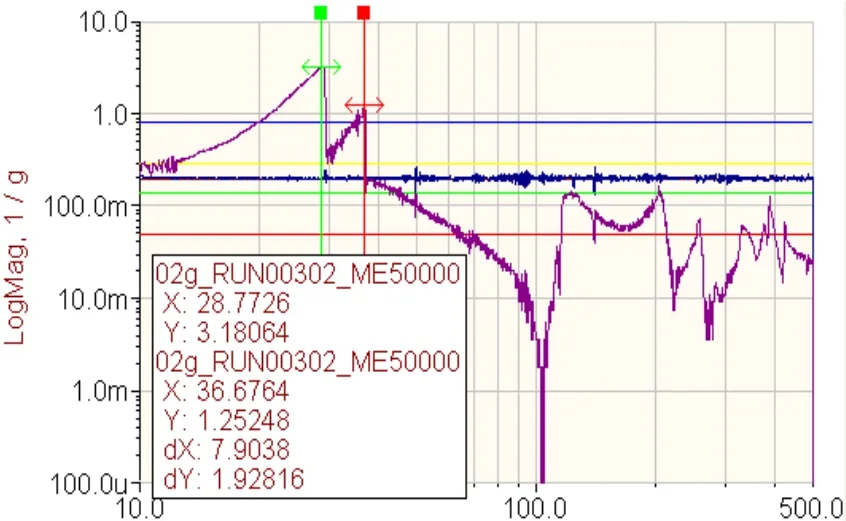
图9　Y向特征试验响应曲线

表4　仿真结果与试验结果比较

由表2可知仿真结果与试验结果误差在8%以内，满足工程分析的要求，说明二维转台的有限元分析结果比较准确，MPC模拟的轴承能用在二维转台的工程分析中；由z向试验曲线可以看到，试验曲线存在毛刺，这是由活动部件轴承的间隙的非线性造成的。

4　结论

二维转台的有限元分析结果与特征试验结果表明，MPC模拟的简支梁中点位移与材料力学计算的中点位移误差在4.1%，说明MPC能比较准确的模拟铰链特性；二维转台在x、y、z三个方向计算的固有频率与试验结

【】【】果误差在8%，说明MPC能较准确的模拟了轴承，适合二维转台的模拟。

参考文献：

［1］ 张欣.美国空间监视系统发展综述［J］.电信技术研究，2001，365：53-61.

［2］ 王杰娟，于小红.国外天基空间目标监视研究现状与特点分析［J］.装备指挥技术学院学报，2006，17（4）： 33-37.

［3］ 姜明，王玉鹏，方伟，等.太阳辐射监测仪跟踪引导系统的设计［J］.电子测量技术，2013，30（9）：84-88.

［4］ 王智，李朝辉.月基极紫外相机光机结构设计［J］.光学精密工程，2011，19（10）：2427-2433.

［5］ 马星国，孙雪，尤小梅.基于ANSYS的滚针轴承的有限元分析［J］.设计制造及质量控制，2008，03，328-332.

［6］ 熊小晋，张晓鹍，熊晓燕.滚动轴承接触的非线性有限元分析［J］.信号检测、算法与仿真，2009，01：23-27.

［7］ 马士垚，张进国.滚动轴承接触问题的有限元分析［J］.机械设计与制造，2010，09：8-9.

［8］ 杜静，等.基于GAP单元的滚动轴承应力分析［J］.机械设计与制造，2011，6：43-45.

Modal analysis and experimental verification of two-dimensional turntable

HE Shuai， WANG Zhong-su

中图分类号：V416

文献标识码：A

文章编号：1009-0134（2016）05-0139-03

收稿日期：2016-01-22

作者简介：贺帅（1989 -），男，研究实习员，硕士，主要从事空间遥感器力学分析工作与机器人运动学、动力学建模工作。