基于Hilbert-Huang变换的往复发动机气门间隙故障诊断方法研究

王立勇，贾 然，陈 涛，李 乐

（北京信息科技大学　现代测控技术教育部重点实验室，北京 100192）



基于Hilbert-Huang变换的往复发动机气门间隙故障诊断方法研究

王立勇，贾 然，陈 涛，李 乐

（北京信息科技大学现代测控技术教育部重点实验室，北京 100192）

摘 要：配气机构是发动机的重要组成部分，若发生故障将会使发动机工作性能大大下降，采用Hilbert-Huang变换的方法对发动机振动信号进行处理。通过计算信号的Hilbert谱、Hilbert边际谱和Hilbert边际能量谱，分析气门间隙变大及变小故障在各种图谱中的表现，证明了HHT方法在气门间隙故障诊断中的有效性。

关键词：故障诊断；Hilbert谱；Hilbert边际谱；Hilbert边际能量谱

0　引言

发动机是一种典型的动力输出设备，已被广泛应用到多种场合，如车辆、舰船、钻井平台等。作为系统的核心动力源，发动机一旦发生故障会直接影响到整个系统的正常运行，造成一定的经济损失。而配气机构是发动机的重要组成部分，其若发生故障会使发动机工作性能大大下降，间接影响到系统的运行。

配气机构工作过程中零部件的磨损会导致气门间隙发生故障，致使发动机的工作性能下降。及时的监测发动机气门间隙大小，保证其处于合理的范围能够使发动机始终以较高的工作性能运行。气门间隙的故障特征主要体现在振动信号中。因此本文采用振动分析法实现发动机气门间隙故障的诊断。

Hilbert-Huang变换方法是一种信号的时频分析方法，能够将信号分解为若干不同尺度的平稳波动或趋势，并使分解后的信号具有真实的物理意义。本文采用Hilbert-Huang变换的方法对发动机振动信号进行处理，实现发动机气门间隙故障的诊断。

1　HHT故障诊断方法

1.1HHT变换原理

Hilbert-Huang变换由经验模态分解（Empricial Mode Decomposicon，EMD）和Hilbert变换两部分组成。其基本过程为：首先采用EMD分解方法将信号分解为若干个包含不同尺度信息的IMF（Intrinsic mode function）分量之和，其次对每个IMF分量进行Hilbert变换，得到信号瞬时频率和瞬时幅值，最后计算得到信号的Hilbert谱和Hilbert边际谱。

1.2EMD分解流程

1）计算信号X（t）所有的局部极值点，采用三次样条曲线将信号局部极大值点进行差值，拟合得到信号的上包络线Xmax（t），同理得到下包络线Xmin（t）。

2）构建上、下包络线的均值线。

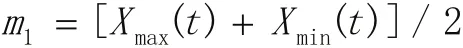
3）计算得到h1（t）=X（t）-m1（t），如果h1满足IMF条件，则h1即为X（t）的第一阶IMF分量。如果h1不满足IMF条件，则将h1作为原始数据，重复以上步骤，得到h11=h1-m11，其中m11为h1的上下包络线的均值。若h11仍不满足IMF条件，则重复循环k次，得到h1k（t）=h1（k-1）（t）-m1（k-1）（t），使得h1k（t）满足IMF条件，则记c1=h1k为第一阶IMF分量。

4）将c1从X（t）中分离出来，得到r1=X（t）-c1，并将r1作为原始数据重复上述模态分解过程，经多次运算即可得到n阶IMF和残差rn（t），完成EMD分解的操作。

EMD方法能够产生有限个IMF分量，且各IMF分量均对应一定的物理过程。在EMD分解过程中若IMF分量判定条件过于苛刻，将使得分解后信号中后几个IMF分量失去物理意义，若条件过于松弛则会使分解过程过早结束，造成分解不彻底，致使信号中部分有意义的信息不能提取出来。为了保证信号得到合理的分解，采用了能量差跟踪法［1］作为IMF分量的判定条件。

1.3Hilbert变换方法

对所有IMF分量进行Hilbert变换，得到每个分量具有物理意义的瞬时频谱，并将其表示在振幅与时间、频率的联合分布上，即得到了Hilbert谱：

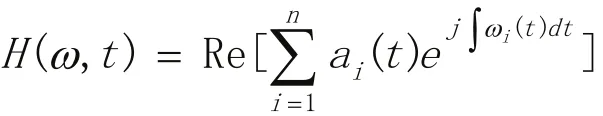
Hilbert谱精确地描述了信号幅值随时间和频率的分布情况。

对Hilbert谱进行时间域上的积分，便可以得到Hilbert边际谱：

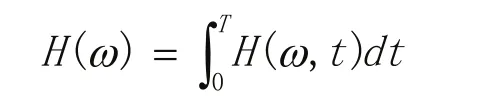
Hilbert边际谱则表征了信号的幅值随频率的变化情况。在Hilbert边际谱中某一频率上出现了振动能量，说明在信号中包含该种频率的振动。其具体出现的位置则在Hilbert谱中给出。

将|x（t）|2看为信号的能量密度，则Hilbert变换后的H2（ω，t）具有能量密度的物理意义。并将H2（ω，t）称为Hilbert能量谱。对Hilbert能量谱进行时域上的积分得到Hilbert边际谱能量为：

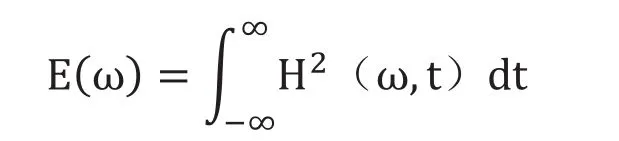
Hilbert边际能量谱精确的描述了信号的能量随频率的分布情况。

1.4基于HHT的发动机气门间隙故障诊断流程

本文主要通过Hilbert谱、Hilbert边际谱及Hilbert边际能量谱进行气门间隙故障特征提取。首先对原始信号进行EMD分解得到多个IMF分量，采用相关系数法滤除IMF分量中与故障无关的低频成分。其次采用剩余IMF分量进行信号重构。最后对重构信号进行Hilbert谱分析。具体方法流程图如图1所示。

2　气门间隙故障分析

2.1气门机构分析

配气机构是发动机重要的组成部分，其主要功能是按照发动机点火顺序和各缸工作冲程，定时的打开和关闭各缸的进排气门。其结构简图如图2所示。

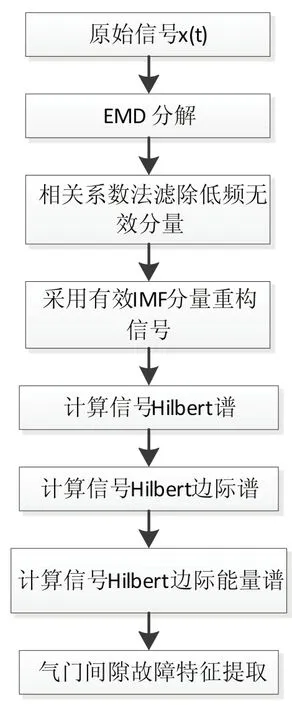
图1　试验方法流程图

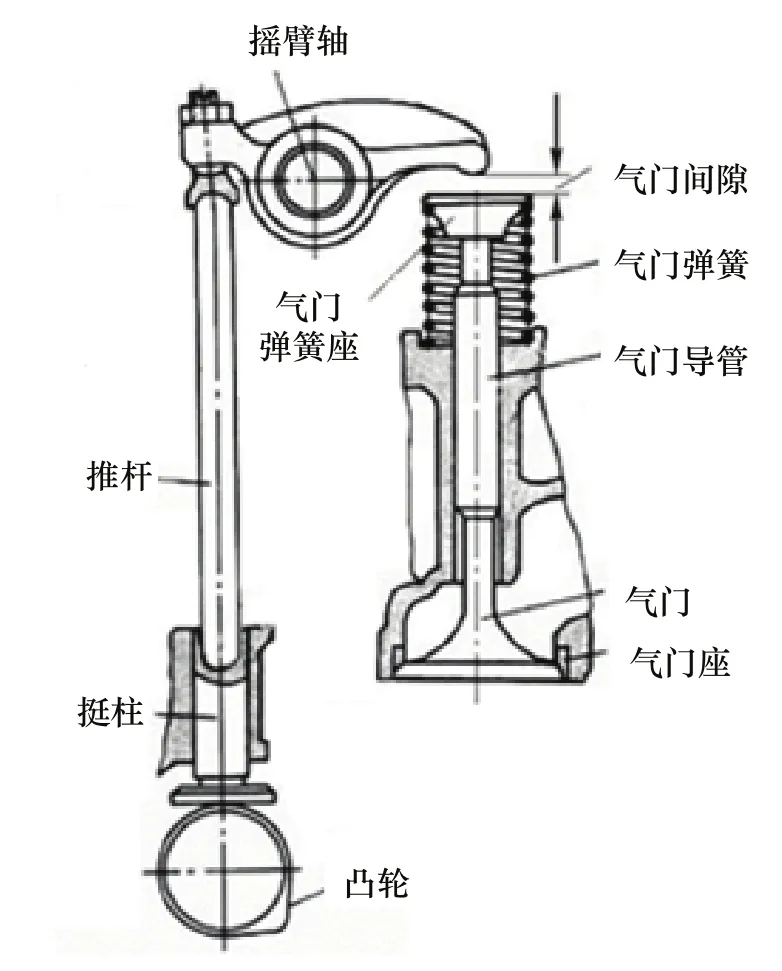
图2　气门结构图

若发动机气门间隙过小，挺柱和推杆受热膨胀时会致发动机气门打开提前，关闭延时，气门开启时间变长，严重时会导致气门关闭不严，造成漏气故障；若气门间隙过大，则会造成发动机气门打开延时，关闭提前，气门开启时间变短，致使发动机进气不充分、排气不彻底，造成发动机产生非正常的振动和噪声，并导致发动机燃烧不充分，影响发动机工作性能。

2.2冲击事件分布

为了研究气门间隙故障时发动机振动信号的变化情况，选择了491Q-ME型发动机进行实验研究。该发动机是一款直列四缸四冲程发动机，其点火顺序为1-3-4-2。根据发动机参数绘制了发动机冲击事件的分布图，如图3所示。图中（a）～（d）为发动机单缸冲击事件发生时刻分布图，（e）为所有气缸冲击事件发生时刻的合成分布图，其中事件a～t分别代表：EVC4、IVC3、EVO1、IVO2、F3、EVC2、IVC4、EVO3、IVO1、F4、EVC1、IVC2、EVO4、IVO3、F2、EVC3、IVC1、EVO2、IVO4、F1（EVC-排气门关闭，IVC-进气门关闭，EVO-排气门打开，IVO-进气门打开）。

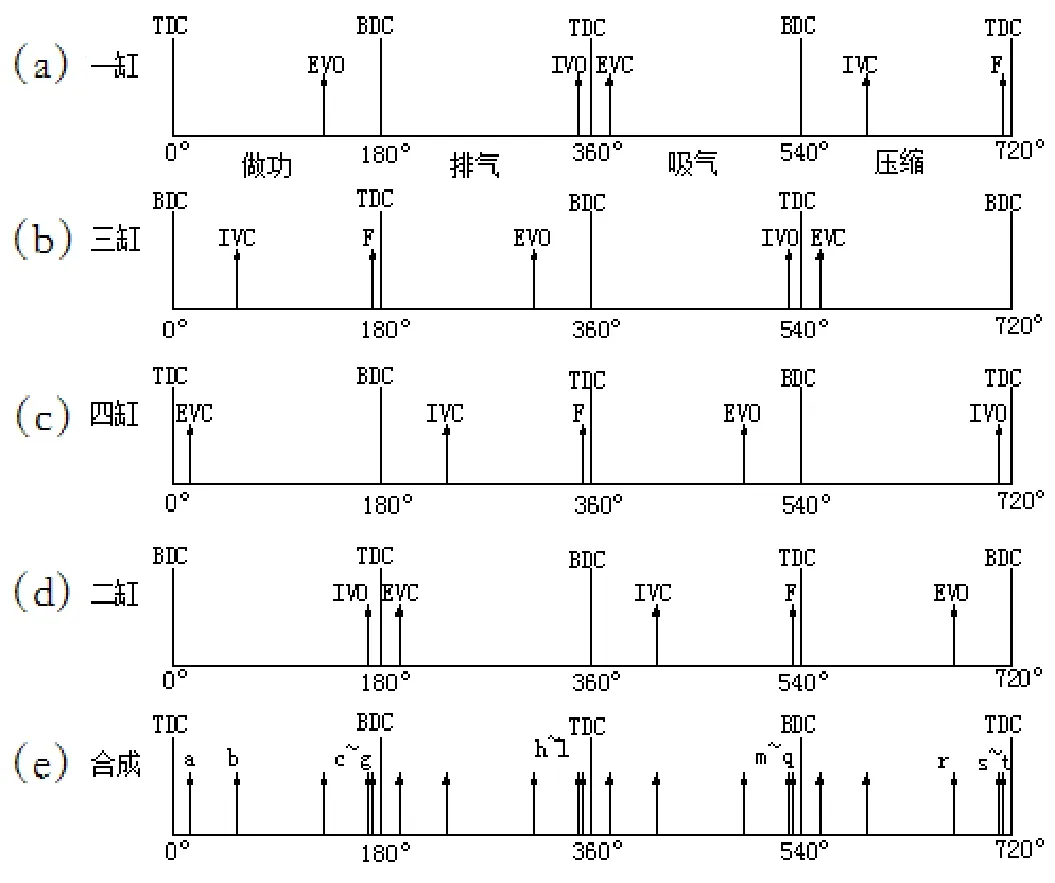
图3　发动机各冲击时间分布图

2.3基于HHT的气门间隙故障诊断实验分析

为了研究气门间隙故障时振动信号的特点，分别将四缸排气门顶杆进行了磨损和加长，以模拟气门间隙变大和变小故障。对正常信号和故障信号进行了对比分析。发动机振动信号如图4所示，图中（a）、（b）、（c）分别为气门间隙正常、间隙变大及间隙变小振动信号。

对信号进行EMD分解，并采用相关系数法滤除IMF分量中无效的低频分量，以气门间隙正常信号为例。表1为各阶IMF分量与原始信号的相关系数ri。可见自第四阶以后的所有IMF分量与原始信号的相关性较差，因此选择前三阶IMF分量进行信号重构，即X（t）=IMF1+IMF2+IMF3，并对该重构信号进行Hilbert谱分析。

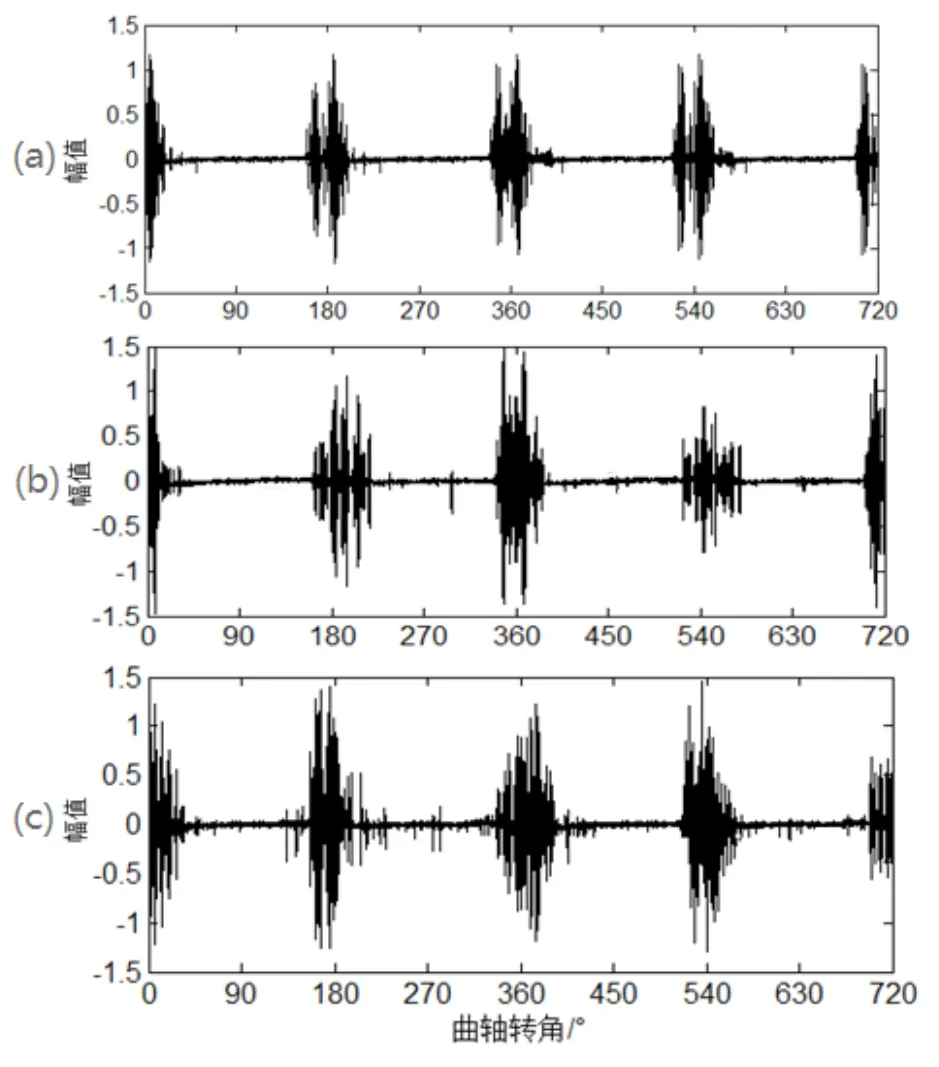
图4　原始振动信号

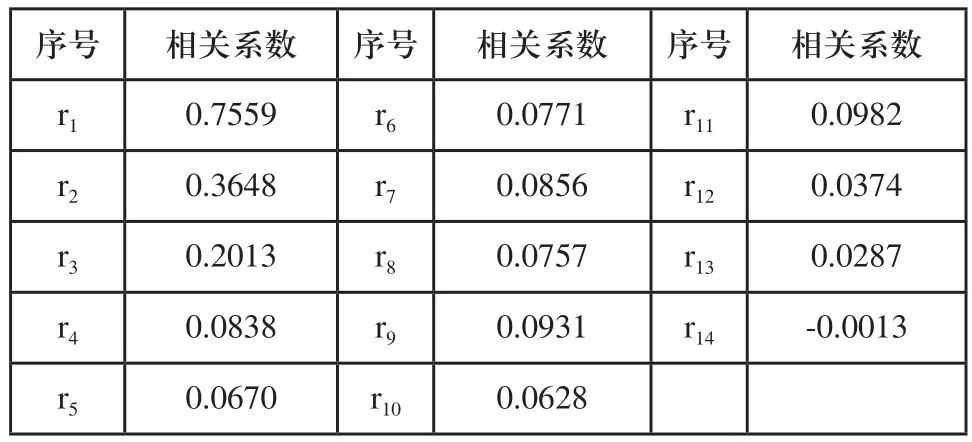
表1　各分量与原始信号的相关系数

重构信号的Hilbert谱如图5所示，其中（a）、（b）、（c）分别为气门间隙正常、间隙变大和间隙变小时信号的Hilbert谱。可见气门间隙正常时四个集中振动区域信号分布情况基本一致，整体表现为0～10kHz处信号振幅较小，在25k～30kHz处信号幅值大。当气门间隙变大时Hilbert谱中曲轴转角0°附近振动的高频成分明显增强。表明在发动机在该位置处产生了强烈的异常冲击。对比发动机各冲击事件分布图可知，该部分异常振动是由于发动机气门关闭造成。当气门间隙变小时，信号没有明显的幅值变化，但仔细观察可发现，在540°区域的信号0～10kHz的信号密度明显加强。因此说明发动机四缸排气门间隙变小使得该处振动信号的低频成分得到了明显的加强。对比发动机各冲击事件分布图可知在540°附近发生了四缸排气门打开事件。

为了更清晰的描述信号的频率分布，计算了发动机三种状态下信号的Hilbert边际谱。如图6所示。图中（a）、（b）、（c）分别为气门间隙正常、间隙变大和间隙变小时信号的Hilbert边际谱图。可见，发动机正常运行时信号于15k～20kHz频率带之间出现较大的振动幅值，33kHz以上频率带振动信号在大大减弱。气门间隙偏大时，信号中振动幅值出现了两个峰值区域，分别位于15k～25kHz处和33k～40kHz处。对比6（a）图可知，信号中频率约为33k～40kHz的大幅振动为气门间隙变大造成故可作为气门间隙偏大故障特征。发动机气门间隙偏小时信号时，信号中频率为0～15kHz频率带的振动成分幅值出现了明显的增强。因此该部分振动可作为气门间隙偏小故障特征。

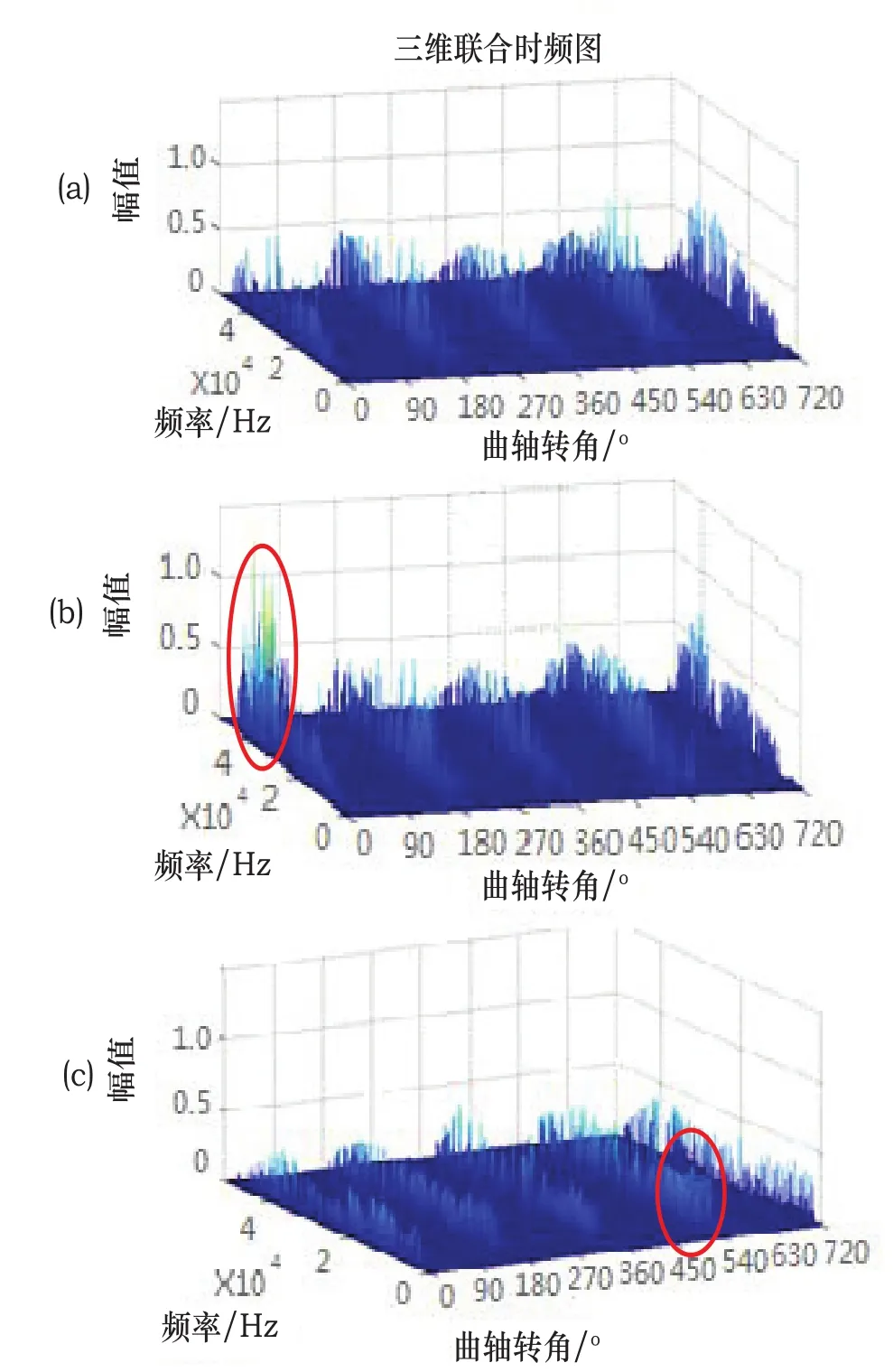
图5　重构信号Hilbert谱

分别计算上述三种情况的Hilbert边际能量谱，分别如图7中（a）～（c）所示。可见发动机正常运行时边界能量谱峰值位于25kHz处，发动机气门间隙变大时边际能量谱峰值分别位于25kHzh和38kHz处，发动机气门间隙变小时边际能量谱峰值位于28kHz处，同时在12kHz处出现了局部峰值。

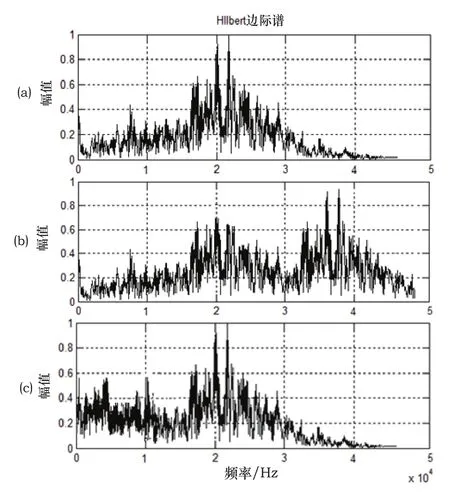
图6　重构信号的Hilbert边际谱

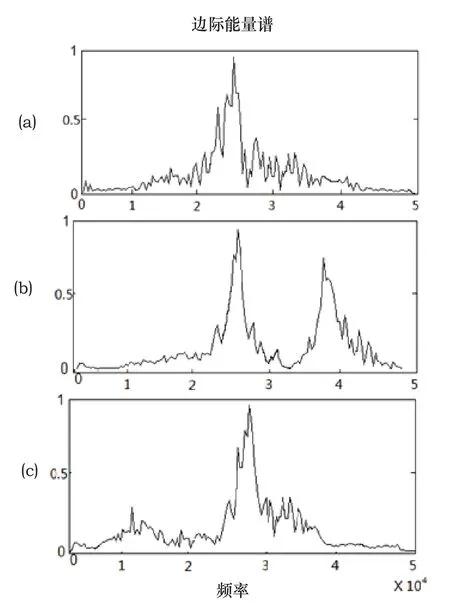
图7　信号的Hilbert边际能量谱

【】【】

分别计算10kHz～15kHz，23kHz～28kHz，37kHz～42kHz频率带处的局部边际能量如表2所示。

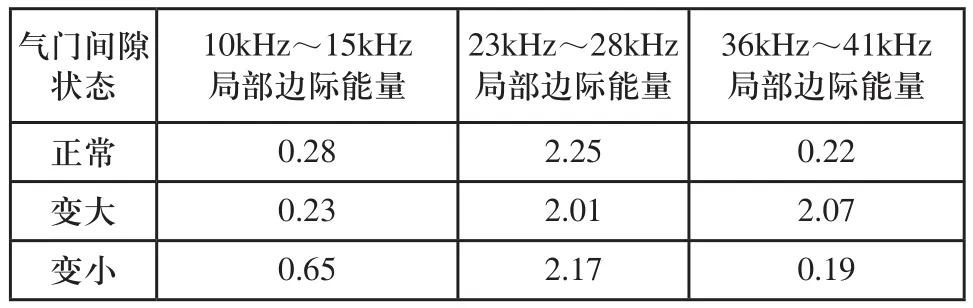
表2　故障特征频率带的边际能量

由表可知，发动机正常运行时信号在23kHz～28kHz内的局部边际能量谱最大，约为2.25，而在两侧的频率带中局部边际能量全部小于0.3，而发动机气门间隙变大故障时，可见在36kHz～41kHz处的局部边际能量大大提高，当发动机出现气门间隙变小故障时10kHz～15kHz处的局部边际能量则也增高至0.65。可见采用上述三个频率段的局部边际能量谱作为故障特征，能够有效的对发动机气门机构进行故障诊断。

3　结论

基于EMD分解方法、Hilbert谱方法和Hilbert边际能量谱的方法对气门间隙故障进行了诊断。提出了发动机发生气门间隙变大故障时会使会使得气门关闭事件位置的高频分量及低频分量振幅增加，使得36kHz～41kHz频率带处的边际谱能量增加。发动机出现气门间隙变小故障时会使得气门打开事件位置处的低频信号的振幅增加，造成10kHz～15kHz频率带处的边际谱能量增加。因此采用Hilbert-Huang变换的方法能够有效的提取故障特征信息，实现发动机气门间隙故障的诊断。

参考文献：

［1］ 于德介，程军圣，杨宇.机械故障诊断的HIlbert-Huang变换方法［M］.北京：科学出版社，2006.

［2］ 王慧.HHT方法及其若干应用研究［D］.合肥工业大学，2009.

［3］ Y.S.Wang，Q.H.Ma， Q.Zhu， X.T.Liu， L.H.Zhao，An intelligent approach for engine fault diagnosis based on Hilbert-Huang transform and support vector machine［J］.Applied Acoustics， 2014，75：1-9.

［4］ YujunLi，PeterW.Tse，XinYang，JianguoYang. EMD-based fault diagnosis for abnormal clearance between contacting components in a diesel engine［J］.Mechanical Systems and Signal Processing，2010，24（1）：193-210.

The research of the fault diagnosis about reciprocating engine valve clearance based on Hilbert-Huang transform

WANG Li-yong， JIA Ran， CHEN Tao， LI Le

中图分类号：TH17

文献标识码：A

文章编号：1009-0134（2016）05-0111-04

收稿日期：2016-01-05

基金项目：国家自然科学青年基金（51105041）；2014北京市优秀人才培养资助-青年拔尖个人项目（2014000026833ZK25）；青年骨干个人项目（2014000020124G096）；北京市教委青年拔尖人才项目（CIT&TCD201404112）

作者简介：王立勇（1977 -），男，副教授，博士，研究方向为机电系统状态检测与故障诊断技术。