航空发动机转子件装配质量预测
2016-07-09孟祥海单福平
孟祥海,单福平
(中航商用航空发动机有限责任公司,上海 200241)
航空发动机转子件装配质量预测
孟祥海,单福平
(中航商用航空发动机有限责任公司,上海 200241)
摘 要:针对航空发动机转子要求高同心度和高可靠性的特点,在公差传递建模中引入周向安装角度这一影响因素,建立了同心度与公差、周向安装角的关系,然后采用蒙特卡罗法对实际装配过程中的合格率进行预测。通过实例计算,证明本方法可以预测航空发动机转子装配的同心度,提高设计的可靠性。
关键词:航空发动机转子;同心度;蒙特卡罗
0 引言
随着航空发动机的推力、转速、动强度等日益提高,结构日趋复杂和重量不断减轻,其安全性、可靠性对于保证发动机性能,提高有效性、出勤率并降低全寿命周期费用至关重要[1,2]。而对于旋转机械来说,转子系统对其可靠性具有重要影响。航空发动机的转子工作在高温、高压环境中,其同轴度对初始不平衡量和转静子碰磨等具有严重的影响,最终会影响整机的振动表现和性能表现,因此要求转子具有高同轴度和高可靠性[3,4]。
目前,转子一次装配成功率并不高,往往需要多次调整或者重新修配后才能保障同心度符合设计要求。为解决此问题,目前的研究主要集中于转子装配阶段的测量与优化技术[3~5],而导致装配成功率不高的源头是在设计阶段。于是,本文尝试建立包含周向安装角度的公差传递模型,采用蒙特卡罗法进行模拟计算,使得设计人员能够预测装配合格率,提高设计可靠性。
1 考虑周向安装角的公差传递模型
航空发动机转子零件是典型的刚性回转体,装配完成后的转子也是回转体,要求同心度越高越好。由于加工制造过程中存在偏差,导致转子零件和装配体都无法成为完美的回转体,从而造成转子装配后的不同心。另一方面,转子零件在装配过程中可以采用不同的周向安装角度,这一操作过程对转子同心度的影响也很大。如图1为两个回转体零件的装配,其中上方零件采用了不同的安装角度,同心度发生了较大变化。
为了将零件公差与安装角度同时考虑到模型中,本文采用连接装配模型(connective assembly model)[6]来表达航空发动机转子件在装配过程中的公差传递关系,并将同心度定义为部件上端面(C2)圆心到中心线的垂直距离,中心线定义为通过部件下端面圆心且垂直该端面的直线(图1)。

图1 周向安装角对同心度的影响
在零件的上下两个端面分别建立坐标系,通过变换矩阵来表示装配过程中不同特征之间的位移和转角变化。在三维空间中,两个坐标系的几何关系如图2所示。从坐标系1变换到坐标系2的过程可用变换矩阵T来表示。变换矩阵同时包含了平移和转动操作,其表达式为:

其中R是3×3的转动矩阵,表示坐标系2相对于坐标系1的转动变换,p是3×1的平移向量,代表坐标系2相对于坐标系1的平移变换,上标T是矩阵的转置符号。

图2 两个空间坐标系的几何关系
对于两个零件的装配,如图3所示。在此将航空发动机转子件的止口装配结构简化,认为装配过程即是将两个零件的端面匹配在一起的过程。在各零件的上下端面建立坐标系,坐标系原点为各端面的圆心,那么端面的匹配过程可用坐标系的变换来表示。

图3 两个零件的装配模型


其中Zi代表第i个零件的高度,i=1,2。将式(3)~式(6)带入式(2),得到:

根据上述推导过程,当有n个零件参与装配时,第n个零件的上端面坐标系相对第一个零件下端面坐标系的变换矩阵为:
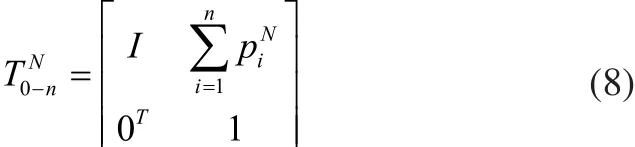
在实际加工制造过程中,零件的端面不可能在名义位置,因此在设计时需要定义公差,公差的存在将导致该端面坐标系发生平移和转动,可以在每一个零件的上端面引入一个变换矩阵来代表公差产生的影响,其形式与式(1)相同。此时,零件2上端面坐标系相对于零件1下端面坐标系的变换矩阵可表示为:


平移误差向量dpi中包含的误差dXi,dYi和dZi,以及转角误差矩阵中包含的误差dθXi,dθYi和dθZi均是以绝对坐标系为参考的,即第一个零件下端面的坐标系。转角误差矩阵为:
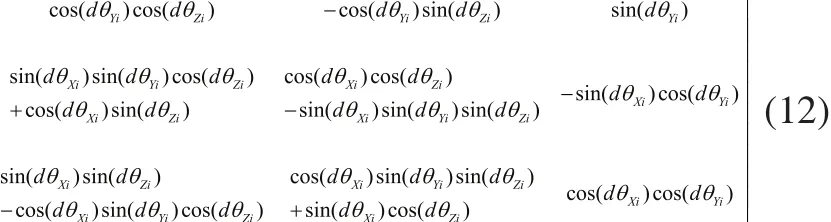
如图3所示,如果两个零件在装配过程中零件2绕Z轴旋转了一个角度θZ2,那么这个角度将反映在变换矩阵T1 1′-中。在这种情况下,同时考虑制造偏差的影响,零件2上端面坐标系相对于零件1下端面坐标系的变换矩阵T0-2表示为:
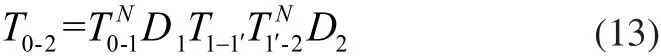
其中:

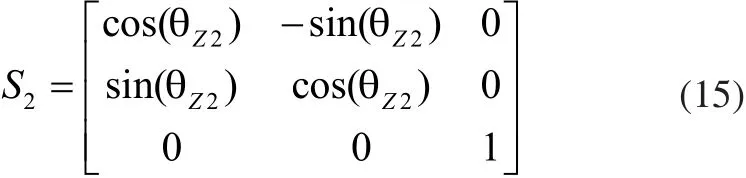
S2即表示转角θZ2对装配结果的影响。
将式(3),式(4),式(6),式(10),式(11),式(14)和式(15)代入式(13),T0- 2可表示为:
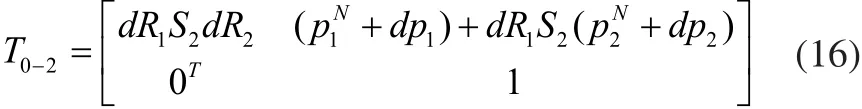
以此类推,当有n个零件装配时,第n个零件上端面坐标系相对于第一个零件下端面坐标系的变换矩阵可以表示为:



2 基于蒙特卡罗法的装配公差分析
目前,公差分析方法主要分为极值法、统计法和蒙特卡罗法。
极值法在计算装配公差时,假定各零件的尺寸同时处于极限值,计算时只需要将各尺寸线性叠加。极值法虽然计算量小、理论简单,但由于所有零件的公差同时处于极值情况的可能性很小,因此该方法通常对装配公差要求过高,要求零件有较小的公差带,以满足设计要求。按照这种方法确定的零件公差偏小,常常导致产品成本升高。
统计法在计算装配公差时,假定各零件公差服从正态分布,装配公差与零件公差之间是线性关系。统计法由于考虑了零件尺寸的统计分布,对实际产品的生产过程的建模更接近于实际。与极值法相比,它可以得到更接近于实际的对装配公差的估计,并允许零件有较宽的公差带。
上一节的建模结果显示,转子同心度与公差、周向安装角为非线性关系;根据实际情况,公差与周向安装角并不一定服从正态分布。蒙特卡罗法能够同时解决这两个问题,因此本文采用蒙特卡罗法进行公差分析。
蒙特卡罗法是一种统计试验计算方法,它是以概率统计理论为基础的一种方法[7]。其基本思想是当所求问题的解是某个事件的概率,或者是某个随机变量的数学期望,或者是与概率、数学期望有关的量时,通过某种试验的方法,得出该事件发生的概率,或者该随机变量若干个具体观察值的算术平均值,通过它得到问题的解。
将蒙特卡罗法用于上一节的公差传递模型进行分析的步骤是:
1)确定各影响因素(零件公差、周向安装角)的概率分布类型;
2)根据模拟精度要求确定随机模拟次数N;
3)根据各影响因素的分布规律和分布范围,分别对其进行随机抽样,从而得到一组已知影响因素的随机抽样;
4)将随机抽样带入公差传递函数,计算同心度,得到该同心度的一个子样;
5)将步骤3)、4)重复N次,即可得到同心度的N个子样,构成一个样本;
6)通过记录同心度符合设计要求的次数,即可预测转子装配的成功率。
3 实例分析
已知零件均为圆柱形回转体,高H=70mm,上下端面直径为W = 1 0 0 m m,平移误差的设计要求为dXi=dYi=dZi≤0.1 mm ,旋转误差的设计要求为dθXi=d θYi=d θZi≤0.002rad ,假设零件误差在加工过程中均服从正态分布,装配过程中周向安装角度随机选择,即服从均匀分布。
那么每一个零件上端面坐标系相对于下端面坐标系的坐标均为(0,0,70),即Xi=0mm,Yi=0mm,Zi=70mm。平移误差服从均值为0.05mm,标准差为mm的正态分布,旋转误差服从区间内的均匀分布。
使用MATLAB编程计算,设定模拟次数为100000次。
若两个零件进行装配,计算得到的同心度概率分布形式如图4所示。当测量要求为同心度不大于0.2mm,则可以预测实际装配过程中的成功率为84.76%。

图4 同心度分布规律A
若三个零件进行装配,计算得到的同心度概率分布形式如图5所示。当测量要求为同心度不大于0.2mm,则可以预测实际装配过程中的成功率为40.20%。
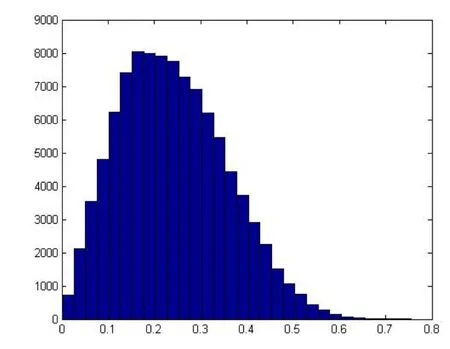
图5 同心度分布规律B
如果将测量要求改为同心度不大于0.3mm,则可以预测实际装配过程中的成功率将提高到70.07%,分布规律如图6所示。

图6 同心度分布规律C
在此基础上,将旋转误差的设计要求缩小到0.001rad,通过计算,装配的成功率将达到95.29%,分布规律如图7所示。
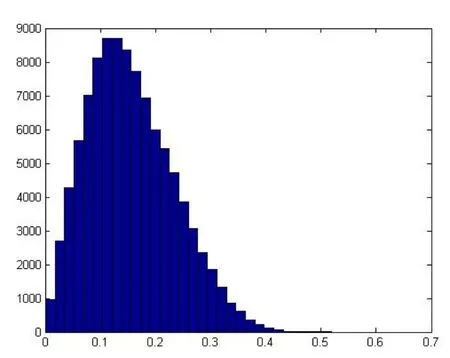
图7 同心度分布规律D
从计算结果可以看出:由于公差的累积效应,零件数越多,同心度越差;为了提高装配成功率,需要综合考虑零件公差和设计要求值的大小,即在合理的范围内适当缩小零件公差,放宽设计要求。
4 结论
本文针对航空发动机转子装配成功率低的问题,建立了包含周向安装角的公差传递模型,采用蒙特卡罗法进行计算,并对实例的装配成功率进行了预测。本文方法将传统的转子公差分析从二维扩展到了三维,同时也将设计与制造联系起来,使得在设计阶段能够提前考虑装配制造阶段的影响因素,提高了设计的可靠性。
参考文献:
[1] 宋兆泓.发动机可靠性工程研究[M].北京:北京航空航天大学,1989.
[2] 费成巍,艾延廷.航空发动机健康管理系统设计技术[J].航空发动机,2009,35(5):24-29.
[3] 刘君,吴法勇,王娟.航空发动机转子装配优化技术[J].航空发动机.2014.40(3):75-78.
[4] 史新宇,吕玉红,吴法勇.整机装配阶段的同心度测量研究现状综述[C].中国贵州贵阳:2013.
[5] 吴法勇,王娟.基于同心度测量的转子不平衡量装配优化技术[A].中国科学技术协会、贵州省人民政府.第十五届中国科协年会第13分会场:航空发动机设计、制造与应用技术研讨会论文集[C].中国科学技术协会、贵州省人民政府:,2013:5.
[6] Whitney D E. Mechanical assemblies:their design,manufacture, and role in product development[Z].Oxford university press,2004:1.
[7] 王晶,石宏,黄笑飞,等.基于蒙特卡罗模拟法的航空发动机装配公差分析[J].沈阳航空工业学院学报.2010,27(4):8-11.
Prediction of assembly quality of aeroengine rotor parts
MENG Xiang-hai, SHAN Fu-ping
中图分类号:V263
文献标识码:A
文章编号:1009-0134(2016)05-0061-04
收稿日期:2015-12-23
作者简介:孟祥海(1982 -),男,辽宁抚顺人,硕士,主要从事航空发动机总体结构设计工作。
