载人航天某装置随机振动响应分析与结构修改
2016-07-09撰文中国航天员科研训练中心刘磊马爱军刘洪英石蒙
撰文/中国航天员科研训练中心 刘磊 马爱军 刘洪英 石蒙
载人航天某装置随机振动响应分析与结构修改
撰文/中国航天员科研训练中心 刘磊 马爱军 刘洪英 石蒙
根据随机振动响应分析基本原理,基于HyperWorks平台对正在研制的载人航天某装置进行随机振动响应分析,分析结果表明关注点的加速度均方根响应值放大倍数满足要求,但是部分安装孔位置处响应均方根应力值过大,根据仿真结果对其提出了局部改进意见,在设计阶段即可对产品进行调整修改,以节省研制周期与成本。本文基于随机振动动力学响应的分析与结构修改可以给同类产品的研制及改进提供参考。
一、引言
航天器在地面运输、发射及飞行等过程中需要经受严酷的振动环境,分为确定性振动(主要为正弦振动)和随机振动两大类,其中随机振动是一种声致振动,主要来源于起飞喷气噪声和运载火箭跨声速飞行及高速飞行时引起的气动噪声。振动环境所产生的破坏作用,轻则导致航天器部组件性能下降,重则导致整个发射任务失败,因而在航天产品的研制过程中,振动是要考虑的重要因素,而通过对结构进行有限元建模然后进行振动响应分析是一种预知结构动态特性的有效方法,可以在产品设计阶段了解结构的振动形式,以利于结构的改进及优化设计,节省研制周期与成本。
随机振动响应分析是产品结构力学特性分析中的重要一步,当结构受到非确定性的连续载荷激励时,可以使用随机响应分析。本文基于有限元分析及优化软件HyperWorks平台,对正在研制的载人航天某装置进行了随机振动响应分析研究,首先进行了结构有限元建模及模态分析,然后利用模态频率响应分析法进行结构随机振动响应分析,得到关注节点的加速度均方根响应值和整体结构响应均方根应力,并将输出节点均方根加速度值与输入值进行比较,响应均方根应力结果与准静态分析应力结果比较,最后根据仿真分析结果给出了结构改进设计建议并应用于产品的研制过程中。
二、基本原理
1.随机振动基本理论
随机振动即为系统的振动运动是不可预知性,其研究承受随机激励时,系统运动的统计特性与激励的统计特性以及振动系统本身动力特性之间的关系。
对于各态历经过程,其自相关函数为:
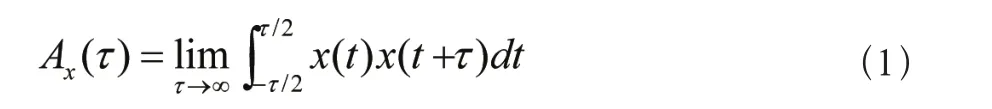
随机振动无法用时间的精确数学式表述,只能用概率论和统计学方法来进行描述。对应的统计量有功率谱密度(PSD)和均方根(RMS)等。
其中其自功率谱密度函数与自相关函数互为傅里叶变换:
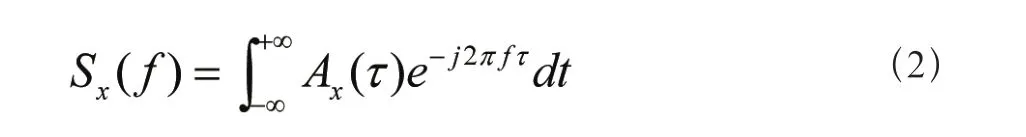
响应的均方根为:

随机振动输出节点相应的功率谱密度函数均可由输入激励的功率谱密度函数与频率响应函数计算得到。问题的求解关键即为求解频率响应函数H(ω),频率响应函数可以通过模态位移法求得。
2.模态位移法
多自由度系统的动力学基本方程为:

对于此复矩阵方程可以使用直接法和模态法进行计算,直接法直接在离散的激励点通过求解(4)式复矩阵方程得到结构的响应u,而模态法首先进行模态分析得到系统的固有频率及振型,可通过求解(5)式得到。

系统的响应u可以表示为模态矩阵Φ和模态坐标η(t)的数量积。

通过(6)式坐标变换,(4)式耦合的动力学方程可以变换为解耦的以模态坐标表示的模态方程(7)式。
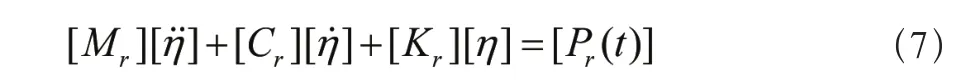
其中Mr、Cr、Kr分别为对应的模态质量矩阵、模态阻尼矩阵、模态刚度矩阵。
通过求解(7)式可以得到模态坐标η(t),代入(6)式即可得到系统响应u。求得结构的响应u,根据频率响应函数H(ω)的定义即可很容易求得。
三、结构有限元建模及模态分析
1.结构有限元建模
正在研制的载人航天某装置是由外部框架结构和内部诸多单机组成,外部框架结构为薄壁梁组成,因而有限元建模采用面网格进行建模,而内部单机为非重点考察对象,为了提高随机振动响应求解效率,对于单机采用质量点在质心处进行模拟,通过刚性单元与单机的框架安装点进行连接。框架之间通过螺栓或焊接进行连接,模型边界条件为通过底板一系列安装孔进行完全约束,最终结构有限元模型如图1所示,框架全部采用铝(2Al2)材料,材料参数如表1所示。

表1 材料参数
2.模态分析
本文利用模态法进行随机振动响应分析,首先可以计算得到模型固有频率及固有振型,分别如表2和图2所示。
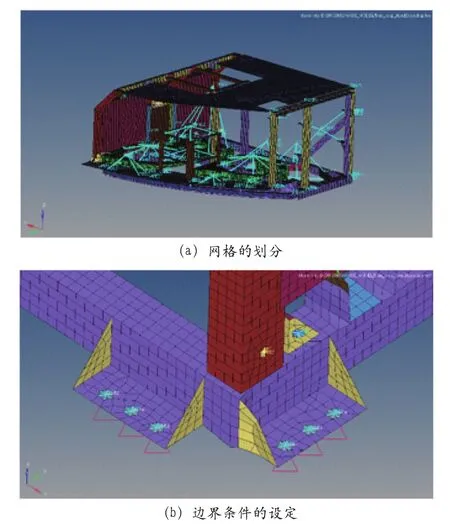
图1 结构有限元模型

表2 结构的前十阶固有频率
分析发现,由于顶部盖板较薄,结构的第一、二、三振型均为顶板的局部振动。第四阶振型为装置的一阶整体振动,频率为51.8Hz,满足设计方给定的大于30Hz的要求,且有较大余量。


图2 结构前六阶振型云图
四、随机振动响应分析
本文采用大质量法模拟随机振动中的基础振动,将受约束的强迫振动转为作用于无约束结构的等效外力。在装置底部中心设置一个节点A,用刚性单元将该节点与框架底部诸多安装孔周围的均布节点连接,同时在该节点设置集中质量单元,施加一大质量,大质量为结构总质量的106倍。随机振动载荷条件采用如表3数据。
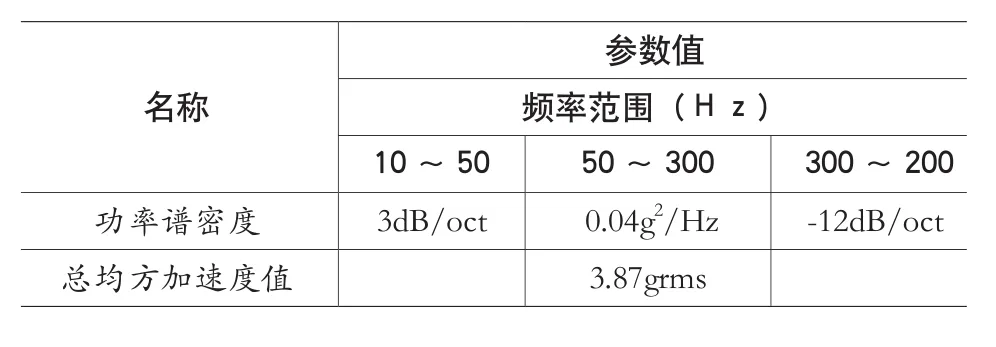
表3 随机振动载荷条件
输入激励选择最为关心的Z向进行加载,输出结果选择最为关心质心节点B、C、D的加速度功率谱密度曲线,如图3所示,同时为了验证输入激励的正确性,也输出施加激励的A节点加速度功率谱密度曲线,结果如图4所示,计算输出节点均方根加速度值及放大倍数如表4所示。通过对结果进行分析判断装置刚度与强度是否满足要求,刚度要求为一阶整体振动频率大于30Hz(上节模态分析结果表明频率满足要求)、组件中单机产品质心节点动响应放大系数小于5,强度符合要求指结构响应均方根应力乘于系数后小于材料屈服应力。
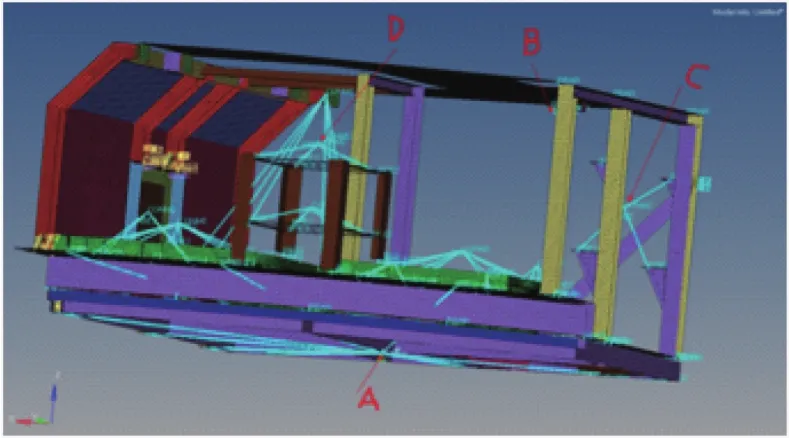
图3 随机振动响应分析输出节点选择
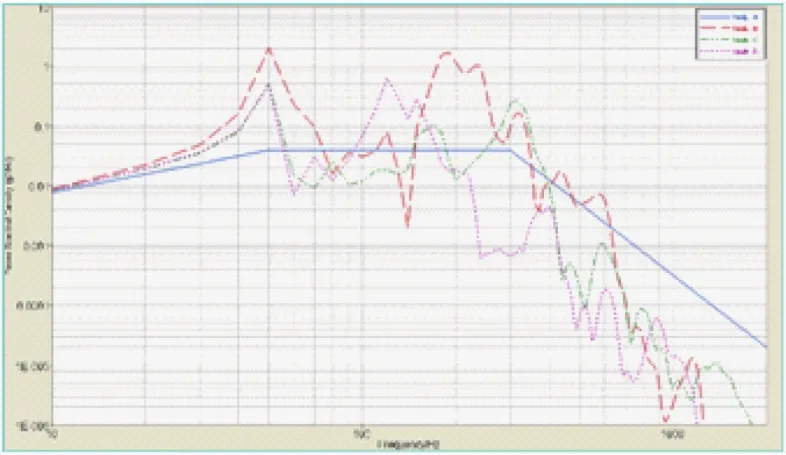
图4 PSD加速度功率谱曲线
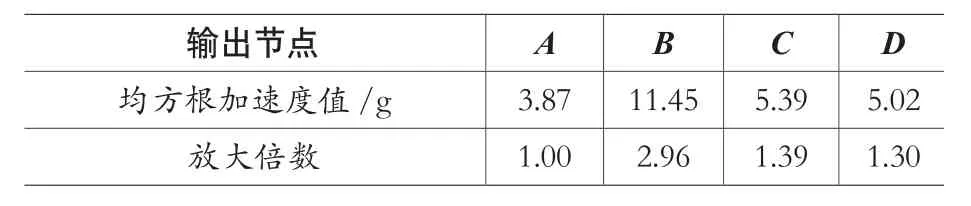
表4 输出节点均方根加速度值及放大倍数
为了识别应力较大区域,输出得到Von Mises应力均方根分布图,如图5所示。应力较大处分布在底部安装孔、中部框安装孔以及顶板与后梁连接处,位置与准静态分析计算结果(图6)一致。随机振动均方根最大应力为122MPa,准静态分析结果最大应力为282.6MPa,均发生在底部安装孔处。

图5 随机振动均方根应力分布云图

图6 准静态分析结果应力云图
五、分析与讨论
对随机振动响应分析结果进行分析可以得到如下结论:
(1)通过对图4分析表明,节点A输出加速度功率谱密度值与表3所给随机振动载荷条件一致,表明输入激励的正确性。
(2)表4输出节点均方根加速度值及放大倍数结果表明,最为关心几个节点均方根加速度放大倍数小于5,表明刚度满足要求。
(3)图5均方根应力分布云图与图6静力学分析应力云图结果一致,均表明应力较大处发生在底部安装孔、中部框安装孔以及顶板与后梁连接处,最大应力值为122MPa,工程上常用3倍均方根应力与材料屈服极限对比来衡量材料是否能满足要求,显然三倍均方根应力值366MPa大于材料屈服极限280MPa,不能满足要求,需要进行改进设计。
通过上述分析可以得知,在给定随机振动激励下,框架整体刚度能满足要求,但某些安装孔位置应力较大,故改进设计可以重点放大安装孔位置处的局部调整。在满足其他要求的情况下,提出了以下改进方案:(1)增大安装孔附近壁厚,如图7所示;(2)增加安装孔的数量,分担承受载荷;(3)材料安装孔处由铝材料更换为强度更高的钛材料。
综合制造、安装、减重等方面考虑选择了方案(1)。利用Pro/ENGINEER对含安装孔局部结构进行重新建模,并导入HyperMesh重新进行计算,结果表明随机振动响应均方根应力最大值由122MPa下降到84.2MPa,调整后结构强度可以满足要求,目前改进设计已应用于产品的最终设计。


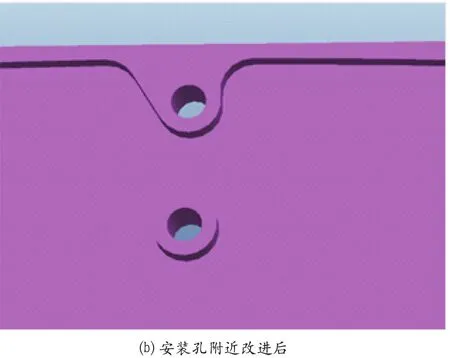
图7
六、结语
(1)对载人航天某装置进行了有限元建模和模态分析,并根据模态频率响应分析法进行随机振动响应分析,得到随机振动载荷条件下,关心节点的加速度功率谱曲线和均方根应力分布云图。
(2)分析结果表明输入激励正确,关心节点的加速度均方根放大倍数满足要求,但部分安装孔附近均方根应力过大,需要进行改进设计。根据仿真结果,选择对结构进行局部调整,计算结果表明改进后结构安装孔附近应力有了明显的下降。
(3)在航天产品设计阶段对其进行动力学特性分析,由此预知结构振动形式,并根据结果对其改进设计可以起到缩短研制周期、节省研制成本的作用,可以给同类产品研制提供一定参考。
