基于CGCS2000的独立坐标系建立与应用

刘博涛，袁凌云，李杰

(石家庄市勘察测绘设计研究院，河北 石家庄　050019)



基于CGCS2000的独立坐标系建立与应用

刘博涛*，袁凌云，李杰

(石家庄市勘察测绘设计研究院，河北 石家庄050019)

摘要：各个城市建设和工程应用中，将实测距离直接投影到国家坐标系中会出现长度变形超限的问题。在分析长度变形产生原因的基础上，介绍了几种独立坐标系建立的类型，并论述每种独立坐标系的特点和适用情况。最后结合案例，阐述了独立坐标系的建立过程，并将工程控制网分别投影到国家统一坐标系和基于CGCS2000建立的独立坐标系中，分别计算对比两种坐标系下长度变形情况，说明所选独立坐标系能够满足工程长度变形限差要求。

关键词：独立坐标系；长度变形；CGCS2000；高程归化；坐标转换

1引言

为了满足国家及周边地区多样性、统一性的测绘需求，我国先后建立了1954北京坐标系、1980西安坐标系等参心坐标系作为国家统一坐标系。依据现行国家标准《城市测量规范》(CJJ/T8-2011)要求城市平面坐标系统应满足边长投影变形值不大于 25 mm/km[1]，而部分地区利用国家坐标系投影后变形值出现不同情况的超限。在当前技术前提下，以国家坐标系为基础建立相对独立的坐标系是控制投影长度变形的有效措施。以往独立坐标系大都基于传统的参心坐标系建立，是二维、非地心的坐标系，存在着精度低、难统一诸多弱点。同时，随着城市区域发展扩大，原有独立坐标系在新区域出现了严重长度变形[2]。随着GNSS技术和大地测量技术的不断发展，2000国家大地坐标系(简称CGCS2000)应运而生。作为新一代地心坐标系，能够大幅度提高测量精度，快速获取精确的三维地心坐标，有利于GNSS与GIS有效的结合，能够为城市大比例尺地形图测量、市政工程施工放样和市政规划等提供方便可靠的数学基础[3]。

2观测边长投影变形分析

观测边长归算到高斯平面需要经过高程归化和高斯投影改化两个过程。高程归化是将地面观测边长归算到参考椭球面；高斯投影改化是将椭球面上的长度投影到平面[4]。

2.1高程归化

地面观测边长一般会高出参考椭球面若干米，将这一边长归算到参考椭球面时必然产生长度变形。假设地面上两点，它们的大地高分别为H1、H2，测得两点间水平距离为S0，将边长测量值归算到椭球面，其长度变形值△S0可按以下公式计算[5]：

(1)

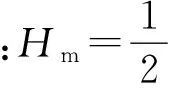
一般来说，将地面边长的水平观测值归算到椭球面后距离会变短。

2.2高斯投影改化

参考椭球是一个不可展平的曲面，实际应用时要把椭球上的元素通过数学方法投影到平面上，我国一般采用高斯投影法。将椭球面上的边长S投影到高斯平面，其长度变形值为△S，可用以下公式计算：

(2)

式中：ym为测线两端点近似横坐标的平均值，Rm为参考椭球面上经改正所得大地线的平均曲率半径。

从式(2)可以看出，△S为正值，且与测线两端点的近似横坐标的平均值ym的平方成正比，即投影边长离中央子午线越远，其变形越大。

3独立坐标系建立的一般类型

经过以上两次改正后，改变了观测边长的真实长度。通过独立坐标系可以减小高程归化与投影变形产生的影响，将其控制在一个微小的范围，进而解决投影变形超限的问题。建立独立坐标系时，应考虑测区所处的地理位置和平均高程，主要有以下4种方法：

3.1国家统一的3°带高斯平面直角坐标系

在进行高斯投影前要估算长度变形值，当两次归化产生的长度综合变形值δ=△S0+△S不超过 25 mm/km时，可直接采用国家3°带坐标系作为该区域的独立坐标系。这是建立区域独立坐标系最理想的情况[6]，测量成果可以直接整合到国家坐标系统中。

从表1变形值分布情况来看，只有距离国家标准中央子午线较近且平均高程面的大地高不大于 150 m的区域或城市可以直接采用国家3°带坐标系。

3.2抵偿投影面的3°带高斯平面直角坐标系

独立坐标系仍采用国家3°带高斯投影，但投影的高程面不再是椭球面而是另选高程参考面，使测区中心地面观测边长归化到该参考高程面减少的长度恰好等于该高程面上的长度投影到高斯平面上增加的长度，通常将选取的这一高程参考面称为“抵偿高程面”。抵偿面的选取可据测区的位置及高程归化和高斯投影两次长度变形量绝对值相等来确定，即令|△S0|与△S相等，则有下式[7]：

(3)

此时，H为测区平均大地高Hm与抵偿面高程H抵之差，ym值取测区中心距标准中央子午线的距离(即横坐标)，RA、Rm可近似认为相等，取当地平均曲率半径；S0、S也可近似认为相等。代入公式可求得H值，进而求得抵偿面高程：

H抵=Hm-H

(4)

抵偿面确定后可认为测区中心的长度变形量可完全被抵消。变动高程归化面，实际就相当于改变了坐标系所对应的椭球，需要计算出该椭球的几何参数。

3.3任意带的高斯平面直角坐标系

这种坐标系是将地面观测值仍旧归化到国家参考椭球面上，但不采用国3°带统一的分带方法，而选择合适的子午线作为中央子午线进行高斯投影，使椭球面上的长度投影到该带的变形恰好抵偿地面观测长度归化到椭球面所产生的变形，我们称这种抵偿长度变形的投影带为“任意投影带”。将式(3)中的H替换回Hm，可求出ym值，进而可确定出任意投影带的中央子午线的位置。3.4具有抵偿面的任意带高斯投影坐标系

当以上3种方法都不能满足要求时，可以采用具有抵偿面的任意带高斯投影法来建立独立坐标系以满足某个区域测量要求。此种坐标系一般以测区平均高程面作为抵偿面，取过测区中心的某条子午线为中央子午线，在中央子午线上选择坐标原点。这样建立的独立坐标系可实现从中央子午线向东、西各横跨约 45 km的长度变形可控范围。

4案例分析

某市东扩经济开发区有一测绘项目，测区位于东经114°41′，北纬38°07′附近，平均正常高70 m，需用GNSS技术布设首级控制网。现布设5个控制点，使用GNSS接收机按外业测量规范进行四等精度静态观测，对观测数据进行后处理获得到精确的WGS-84大地坐标，将WGS-84大地坐标投影到合适的平面坐标系中求得到平面坐标。

如果直接投影到国家标准3°带坐标系中，则测区属于第38带，其标准中央子午线为114°00′00″经线。根据长度投影变形值不超过 25 mm/km的要求，计算国家坐标系满足长度变形要求的范围，公式如下：

(5)

取RA≈Rm≈6 371 km，Hm=55 m，可求出ym在中央子午线以东的取值范围为0 km～52.2 km，测区不在控制范围内，所以需要考虑独立坐标系，如图1所示。

2000国家大地坐标系启用后，该市采用任意带高斯投影法，基于CGCS2000椭球，以椭球面为投影面，东经114°45′00″为中央子午线建立了新的地方独立坐标系。此独立坐标系中央子午线接近测区，高程投影面接近测区平均高程面，将控制带内WGS-84大地坐标投影到此独立坐标系，具体步骤如下：

(1)求解坐标转换参数

在测区附近选择4个具有2000国家大地坐标的求参点，用GNSS静态观测方法获得其WGS-84大地坐标，根据最小二乘原理求解两坐标系间布尔莎七参数转换模型。

(2)计算控制点的2000国家大地坐标

将该工程5个控制点的WGS-84大地坐标(B84，L84)通过求解的转换参数转化为2000国家大地坐标(B2000，L2000)。

(3)计算独立坐标

将(B2000，L2000)通过高斯投影正算公式投影到该市独立坐标系中，计算中涉及的椭球参数采用CGCS2000椭球参数[8]。

按以上所述步骤，用MATLAB 7.1软件编写计算程序，分别求得该工程5个控制点在国家标准投影带坐标系和地方独立坐标系下的坐标值，如表2所示：

对控制网分别在国家坐标和独立坐标框架下进行边长反算，并与实测边长对比，计算出长度变形值和变形相对误差，具体数值如表3所示：

通过表3数据可以看出，该工程控制网采用国家统一坐标系其投影长度变形值相对误差最小为 29.9 mm/km，最大为 40.1 mm/km，已经不同程度超出了 25 mm/km的标准，所以需要建立地方独立坐标系来控制投影变形。新建独立坐标系投影长度变形值相对误差最大仅为 9.2 mm/km，较好地控制了投影变形。同时，该工程控制网直接投影到该市新建独立坐标系下，可以方便工程测量成果统一管理应用以及后续不同坐标系下数据整合。

5结语

对一个区域或一个项目建立控制网，在高斯投影之前必须进行长度变形分析。若长度变形超限，需要根据所测区域具体情况通过调整投影带和抵偿面的方法建立独立坐标系。本工程所采用的独立坐标系是在CGCS2000椭球的基础上建立，与 2000国家大地坐标系之间可通过严密的数学公式相互变换，无任何精度损失。随着2000国家大地坐标系的推广使用，建立在地心椭球下的独立坐标系将会为区域工程建设提供更好的基础服务[9]。总之，在满足长度变形要求的同时，尽量选择易于和国家大地控制网建立联系，便于使用和管理的独立坐标系。

参考文献

[1]CJJ/T8-2011. 城市测量规范[S].

[2]郭春喜，李东. 基于CGCS2000建立城市相对独立坐标系统的方法[J]. 测绘通报，2012(10)：5～7.

[3]田桂娥，宋利杰，尹利文等. 地方坐标系与CGCS2000坐标系转换方法的研究[J]. 测绘工程，2013，23(8)：66～69.[4]孔祥元，郭际明，刘宗泉. 大地测量学基础[M]. 武汉：武汉大学出版社，2006.

[5]赵建三，封良泉，陈宗成. 具有抵偿面的任意带高斯投影法的应用[J]. 工程勘察，2009，7：59～62.

[6]施一民. 建立区域坐标系问题的我见[J]. 测绘工程，2003，9(1)：38～41.

[7]杨元兴. 抵偿高程面的选择与计算[J]. 城市勘测，2008(2)，72～74.

[8]孙勇军. 基于CGCS2000的地方坐标系统建立方法研究[D]. 西安：长安大学，2012.

[9]黎彬，黄校，李秀龙. 基于CGCS2000建立珠海市城市相对独立坐标系统的探讨[J]. 城市勘测，2014(1)：117～121.

The Establishment and Application of Independent Coordinate System Based on CGCS2000

Liu Botao，Yuan Lingyun，Li Jie

(Shijiazhuang Institute of Surveying，Mapping & Geotechnical Investigation，Shijiazhuang 050019，China)

Key words：independent coordinate system；length deformation；CGCS2000 coordinate system；datum plane reduction；coordinate transformation

Abstract：During various urban construction and engineering applications，the length deformation of measured distance maybe exceeds the limit if projected to the national coordinate system directly. Based on the analysis of the length deformation causes，it introduced several types to establish independent coordinate system，and discussed the characteristics and application of each type. Finally，it described the process of establishing an independent coordinate system. The engineering control network was projected to national coordinate system and independent coordinate system based on CGCS2000 separately. It shows the selected independent coordinate system can meet the requirements of length deformation.

文章编号：1672-8262(2016)03-118-03

中图分类号：P226.3

文献标识码：B

*收稿日期：2015—11—21

作者简介：刘博涛(1987—)，男，硕士，助理工程师，主要研究方向是大地测量与数据处理。

基金项目：石家庄市建设局科研项目(0807)