满意度动态加权法在多目标拓扑优化中的应用研究

王海光

（重庆交通大学机电与汽车工程学院，重庆 400074）



满意度动态加权法在多目标拓扑优化中的应用研究

王海光

（重庆交通大学机电与汽车工程学院，重庆 400074）

摘 要：为了研究结构多目标拓扑优化中构造不同评价函数对优化结果的影响，以商用车车架为模型，分别建立了线性加权法、平方和加权法和折衷规划法三种不同的带有权重的目标函数，同时将决策论中满意度理论引入多目标拓扑优化的评价函数的构造中，该方法可以使权重比的设定随每次迭代结果调整，从而消除多工况权重比对优化结果的影响，避免传统方法中人为设定权重比对优化结果造成的偏差，使对比分析结果更加合理。

关键词：多目标优化；满意度；多工况

10.16638/j.cnki.1671-7988.2016.04.016

CLC NO.: TH12Document Code: AArticle ID: 1671-7988 (2016)04-45-03

引言

近年来，拓扑优化研究中多目标拓扑优化问题的研究比重越来越大，在工程中结构多目标拓扑优化问题常通过构建评价函数，将多目标优化问题转变为评价函数的单目标优化问题进行求解。显然，如何建立合理的评价函数是实现结构多目标拓扑优化的关键[1]。范文杰等人[2]采用折衷规划法建立多目标拓扑优化的评价函数，并将此数学模型应用于汽车车架结构，同时提高了车架的动态振动频率和结构刚度。李所军等人[3]以揉度为目标，体积分数为约束，采用优化准则法构建评价函数进行优化。

对于同一个研究对象，针对多个设计目标，可以采用不同的评价函数，而各种不同的评价函数得到的优化结果也会存在差异[4]，对于这些优化结果差异的研究却没有得到足够的重视，孙晓辉等人[5]以汽车悬挂系统的摆臂结构为模型，建立五种不同的评价函数数学模型，通过对五种优化模型设计结果的对比分析，说明不同优化模型的优劣。孙哲[6]以压缩机支架结构为模型，建立了三种不同的带有权重的评价函数，取不同权重系数时，比较三种不同评价函数之间的优化结果。但以上文中评价函数中各工况之间的权重系数是根据经验设定的某一特定值，即权因子是静态的，在权重系数发生变化时，会影响最终的对比分析结果。基于上述缺陷，本文通过引入决策论中的满意度理论，将权重系数由静态的转变为动态的，消除权重对优化结果的影响，建立了含有满意度的三种不同的带有权重的评价函数，并通过对比分析最终的优化结果，说明各不同评价函数在满意度理论下的差异及优劣。

1、多目标拓扑优化评价函数

处理多目标拓扑优化的方法常见的有约束法，分层序列法，评价函数法等[7]。其中，评价函数法是将多个分目标转化为一个数值的函数，即是评价函数，也称为目标函数，然后通过对评价函数的优化，将多目标问题转化为单目标来求解[8]。本文以商用车车架为模型，以车架的揉度和动态频率为目标，同时考虑商用车行驶过程中最常见的三种典型工况：弯曲工况，右前轮悬空和右后轮悬空，分别采用线性加权法，平方和加权法和折衷规划法来建立多目标拓扑优化的评价函数。

1.1 线性加权法

线性加权法是处理多目标优化问题常用的一种比较简便的方法。本文中建立的线性加权法数学模型如下：Minimize：

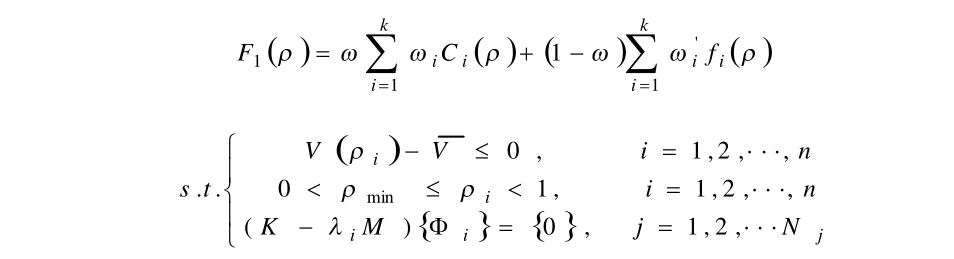
式中：Ci(ρ ) 为第i个工况的揉度目标函数，ωi为第i个工况的权重系数，fi(ρ )为第i阶频率目标函数，ωi'为各阶频率的权重系数，因为本文只考虑商用车行驶的三种工况和前三阶频率，所以k取1,2,3。ω为频率与揉度两目标之间确定的权重值，这里取值为0.5。

1.2 平方和加权法

平方和加权法首先需要求出各分目标单目标拓扑优化时的最优解，再引入权重系数，消除量纲后，通过迭代计算，最终找到使各分目标尽量最优的理想点。本文建立的平方和加权法数学模型如下：Minimize：

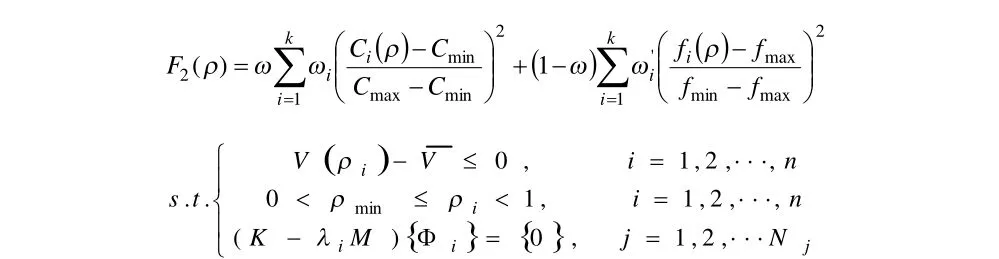
式中Cmin和Cmax分别为揉度单目标优化所得到的最小揉度和最大揉度，fmin和fmax为频率单目标优化所得到的最小频率和最大频率。

1.3 折衷规划法

折衷规划法是目前运用最为广泛的构建目标函数的方法，结合平均频率公式，可以得到满足各分目标的最优解。本文建立的折衷规划法数学模型如下：Minimize：

2、满意度动态权重设计

2.1 满意度的引入

本文中建立了满意度q和不同迭代值Ci(ρ )和fi(ρ )之间的函数关系式如下：

式中：a1和a2的取值分别为2和4，Cil和fil是第i个分目标的最坏值，Cid和fid是第i个分目标的最理想值。

2.2 权重的动态设计

权重因子iω和'iω分别表示是各工况和各阶频率间的重要程度。本文将权重的设计和满意度结合，建立权重因子和满意度之间的函数关系，研究满意度动态权重下，各构建不同目标函数方法的可行性，再对优化结果比较，分析满意度动态权重下，不同目标函数对车架揉度和频率的影响。本文构建的权重因子表达式如下：

结合（1），（3）可以发现，当分目标Ci接近其最优值Cid时，qi就会增大，相应的造成1-qi减小，从而使此分目标对应的权重因子iω减小，当进入下一步迭代时，主要会向权重因子大的分目标的方向进行，从而使该分目标的优化速度下降，相当于一个惩罚因子，自动调节了各分目标的权重因子，使各分目标达到了优化过程中的综合平衡。使用这种方法，可以在迭代过程中，权重因子随迭代值变化，且调节了各分目标之间的重要程度，当分目标接近最优值时，就自动减小其权重，减小向此方向的优化速度，相反，则自动加大权重因子，加大优化速度，使迭代过程连续寻优，最终找到各分目标都满意的最优值。此外，这种方法消除了权重的影响，较为有利的去判断各方法在此动态权重下的优劣。

3、车架有限元模型建立

3.1 车架模型建立

本文建立的商用车车架模型轮廓总长5700mm，宽780mm，高为120mm，在CATIA中建立实体模型后导入HyperWorks中，采用PSOLID三维实体单元对其进行网格划分，划分网格时，将设计空间分为设计域和非设计域，优化时，不改变非设计区域的形态，只在设计区域中挖掉多余的部分，剩余形状即为最后的优化结果。车架所选材料为16Mn，弹性模量E=2.1´1011Pa ，泊松比μ=0.3，密度ρ=7900kg/ m3，最终的有限元模型如图1所示：图中绿色区域为设计域，红色区域为非设计域。

3.2 车架的边界条件和载荷

汽车在行驶过程中，车轮是纯滚动的，当在平坦路面行驶时，即是对应车架的弯曲工况。此工况下，后悬架前支撑限制车架的纵向自由度，横向自由度和垂直自由度，其余支架只限制铅垂自由度。车架的其余两种工况属于弯扭联和工况，模拟的是汽车在不平坦的路面上行驶，某一车轮悬空而抬高的受力状态，此时，释放对应车轮处的约束，其余约束保持和弯曲工况一致不变。

本文车架所受的基本载荷主要归纳为：驾驶室总成和驾驶员重量，共4800N，平均分配到驾驶室前后支撑位置。发动机总成重量1800N，前后分成两部分承载，平均分配到发动机前后支撑位置。满载时，车厢和货物总重量48000N，设定车架承载影响系数为0.75，所以实际承受载荷48000× 0.75=36000N，垂直作用于车架与货箱装配的位置，即车架红色区域后端。载荷情况及边界条件如图2所示：

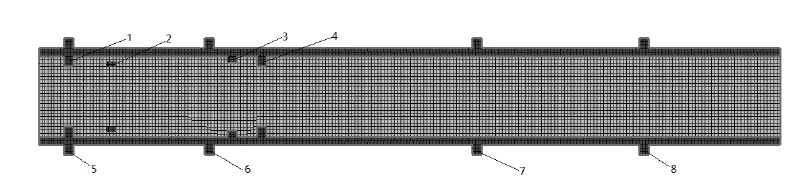
图2　车架的边界条件和载荷

4、优化结果及对比分析

4.1 优化过程及结果

本文在HyperWorks软件中进行优化，先以各工况的刚度最大为目标进行单目标优化，这里将刚度最大转变为应变能最小，即揉度最小，确定各工况下的Cmin的值，而优化前的揉度值即为Cmax。三工况单目标拓扑优化的Cmax和Cmin数据如下。

表1　三工况单目标优化数据结果

随后再分别以一、二、三阶的固有频率最大为目标进行单目标拓扑优化，优化结果得到fmax的值。而优化前各阶固有频率值为fmin，前三阶固有频率单目标拓扑优化的fmax和fmin数据如表2所示：

表2　前三阶频率单目标优化结果

在HyperWorks中迭代计算，得到三种方法在满意度动态加权下的优化结果。优化结果如下图3至图5所示：

图3　折衷规划法

图4　平方和加权法

图5　线性加权法

4.2 优化结果的对比分析

由上图可知，三种方法建立的数学模型，均能实现车架的拓扑优化，且各方法优化后的几何构型相差不大，正如表三和表四所示，这和最后的目标揉度，频率的优化结果数据基本相同相照应。同时，优化结果是不受权重系数所影响的，是在动态中寻优所达到的最优值。根据表三和表四可以对比分析得到，结合满意度动态加权，消除权重影响，线性加权法对车架结构的揉度优化效果明显，折衷规划法使车架结构的频率优化达到最大。最终优化目标数据结果如下表所示：

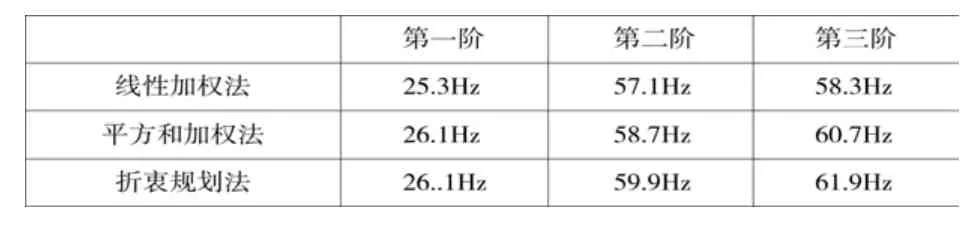
表3　频率优化结果

5、结论

本文采用满意度动态加权法，消除了多目标拓扑优化目标函数中权重的影响，使线性加权法，平方和加权法，折衷规划法三种方法的多目标拓扑优化得以实现，同时通过对比分析三种方法的优化结果发现：

1）在满意度动态加权下，三种方法优化后的几何构型差别不大，其中线性加权法的优化后几何构型有稍许差别，这与揉度，频率优化后结果数据相差不大所对应。

2）在满意度动态加权下，线性加权法对车架刚度的优化效果较显著，而折衷规划法对车架频率的优化效果明显。实际问题中，可以选择适合的优化方法，对优化结果有重要影响。

参考文献

[1] 孙靖民主编，机械优化设计[M]：第4版，北京；机械工业出版社，2008,190-202

[2] 范文杰,范子杰,苏瑞意. 汽车车架结构多目标拓扑优化方法研究[J]. 中国机械工程,2008,12:1505-1508.

[3] 李治多,王明强. 多工况载荷下连续体结构拓扑优化设计研究[J].现代制造工程,2008,09:70-73+124.

[4] 李所军,高海波,邓宗全. 摇臂探测车悬架多工况拓扑结构优化设计[J]. 哈尔滨工程大学学报,2010,06:749-754.

[5] 孙晓辉,丁晓红. 结构多目标拓扑优化设计[J]. 机械设计与研究,2012,04:1-4+9.

[6] 孙哲. 基于多目标拓扑优化的汽车零件轻量化设计[D].华中科技大学,2014.

[7] 汪兵兵,丁晓红,孙晓辉,张横. 机械基础结构多目标拓扑优化设计方法[J]. 包装工程,2013,15:15-18+39

[8] 刘林华,辛勇,汪伟. 基于折衷规划的车架结构多目标拓扑优化设计[J]. 机械科学与技术,2011,03:382-385.

中图分类号：TH12

文献标识码：A

文章编号：1671-7988(2016)04-45-03

作者简介：王海光，就读于重庆交通大学机电与汽车工程学院。

Application research of satisfaction dynamic weighting method on the optimization of multi-objective topology

Wang Haiguang
( College of Mechatronics＆Automotive Engineering, Congqing jiaotong University, Chongqin 400074 )

Abstract:To study the effect of different evaluation functions on the optimization results, a commercial vehicle frame as a model, three methods,namely weighted linear sum method,weighted squares method and compromise programming method applied to construct three mathematical models, respectively,at the same time, the theory of satisfaction degree is introduced into the evaluation function of multi-objective topology optimization.this method can be adjusted as the change of every object after each optimization, to avoid the deviation caused by the weight ratio which is setted by traditional method to the optimization results, to make the comparative analysis of the results more reasonable.

Keywords:multi-objective optimization; satisfiability; multi-load cases