追求自然的数学教学——“对数的换底公式”的教学设计与反思

王　培

(江苏省如东高级中学，226400)



○教学研究○

追求自然的数学教学
——“对数的换底公式”的教学设计与反思

王培

(江苏省如东高级中学，226400)

一、基本情况

1. 学情分析

授课对象为高一普通班学生.学生能够熟练掌握指数对数互化,并进行同底对数的运算，有一定的观察、探究能力.

2. 教材分析

所用教材为《普通高中课程标准实验教科书·数学(必修1)》(苏教版).学生在此之前,已经学习了对数的概念、同底对数的运算性质.本节内容是对数的第三节课换底公式，让学生掌握换底公式是本节课的重点,也是难点.通过换底公式的应用,让学生感悟化归与转化的数学思想.教学目标是让学生掌握对数的换底公式,会用换底公式将一般对数化为常用对数或自然对数,并进行一些简单的化简与证明.

二、教学设计

苏教版必修1教科书第77页，用这样一个问题来进行引入：“试用常用对数表示log35”.这样的设计显得有些突兀,不自然.

数学教学首先要让学生感到数学是自然的.这种自然包括理解数学知识是自然的，数学知识的生成过程是自然的，学习数学知识的范围是自然的，掌握数学思想方法也是自然的.

那么，怎样使学生感到对数换底公式的学习是自然的呢?对此，笔者进行了一些思考:本节课是运算法则课,运算法则实际上解决三个问题:一是这是种什么运算?二是这种运算从哪里来(运算法则产生的必要性和科学性)？三是这种运算用到哪里去(运算法则的数学应用)？

回看对数的三节课内容,我们不难发现其中的数学本质:对数的概念(指数与对数的互化)是解决对数问题的基本依据,同底对数的运算性质只能应用到同底的对数加法、减法和数乘运算,有一定的局限性.这些，自然地引出一些思考:不同底的对数怎么运算?同底的对数能不能做乘除运算呢?

有了这样的思维冲突,引入对数的换底公式就显得“水到渠成”.

1. 问题引入

师:请同学们回顾前两节课我们学习的内容:对数的概念和运算性质.

师:下面请同学们解决以下三个问题：

(1)log182+log189=______；

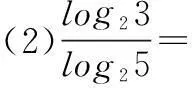
(3)log23×log34=______.

生1:第一题等于1,第二题和第三题不好算.

师:为什么不好算?

生1:因为第二题是同底的对数相除,没有这个法则;第三题是对数相乘,而且是不同底的对数,也没有这样的法则.

师:观察得很仔细.那么同底的对数相除是什么结果?不同底的对数怎么计算?这就是本节课我们要研究的内容.

设计意图上述问题引入,一下子就调动了学生的思维积极性.当学生已有的知识不能解决问题2、3时,学生自发地感受到需要有新的运算法则来补充；同时,在问题3的处理上,学生有意识地认识到需要转化为同底的对数.怎样将不同底的对数转化为同底的对数呢?自然地引出了本节课的课题.

2. 数学建构

探究换底公式

师:先看这道例题:试用常用对数表示log35.怎样用以10为底的对数表示呢?

生2:根据对数的定义,设log35=x,则

3x=5.

师:很好.现在得到了指数式,怎样得到对数式呢?

学生答不出来.

师:我们前面学过,对数不仅是个数,还是种运算,从运算的角度看，这里我们怎么得到以10为底的对数呢?

生3:两边取常用对数,得lg3x=lg5

xlg3=lg5.

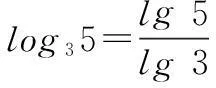
师:非常好.这样我们将log35用以10为底的对数表示,同学们想想,能不能用自然对数表示?是什么形式?

师:很好.更为一般的,我们可以猜测logaN=?,并证明.

学生小组合作,很快得到了结论.

生5刚回答完问题,就有学生举手.

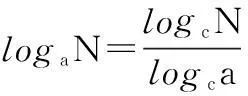
师:同学总结得非常好,这样我们就得到了今天我们所要学习的内容:对数的换底公式.(教师板演)请同学们思考换底公式的特征?我们如何记忆?

师:同学们现在你能解决本节课刚开始的第2、3两道题吗?

=2.

设计意图从特殊的问题入手,让学生直观感受到为什么这样解决和怎样解决,具体的数据,让学生清晰地了解到运算的一般流程,从而对于老师提出的更为一般的问题:“logaN=?”则显得从容很多.得到对数的换底公式后,再回顾反思,解决本节课开始未能解决的两道题目,让学生初步体会换底公式的应用.

探究换底公式的推论

师:在实际的对数运算中,我们还常常用到以下推论.请同学们翻开课本第80页,完成第11题的证明.设a,b均为不等于1的正数,利用对数的换底公式证明:

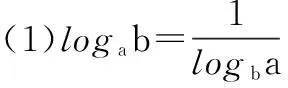
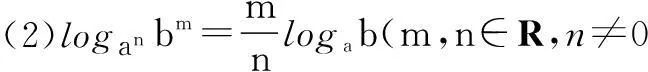
学生的证明过程略.

师:对于第1个式子可以改写为logab×logba=1；

对于第2个式子,当m=n时,loganbm=logab.

师:请同学们思考下,这两个推论有什么意义?

生8:第一个推论说明了logab与logba的关系,是互为倒数关系；第二个推论是将底数与真数的指数都拿出来当新对数的系数,其中真数的指数当分子,底数的指数当分母.

师:,说得也很好,同学们记住他刚所讲的记忆法则了吗?

同学们齐答:记住了.

师:对于第2个式子,当m=n时,loganbm=logab又有什么意义呢?

生9:若底数和真数可以写成幂的形式,且指数相等,则底数和真数的指数可以去掉,结果不变.

师:你能举例说明吗?

生9:比如log2516=log5242=log54.

设计意图对数的换底公式的推论(或变形公式)很多,到底介绍多少为宜?怎样介绍给学生,是生搬硬套地让学生死记?还是让学生巧记?笔者经过认真思考,巧妙地利用教材中的题目,让学生先证明,后观察这两个式子的特点.当学生成功地证明出两个等式,完成初识公式第一步,学生观察总结式子特点后,达到再识公式第二步,当老师举例请同学们计算时,公式记忆再次加强,达到掌握公式应用的第三步.

3.数学应用

例1求值

(1)log89×log332；

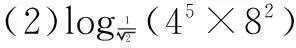
(3)51-log0.23.

师:通过几道题目的训练,请同学们总结对数运算的技巧.

设计意图例1题(1)让学生再次应用换底公式;题(2)是课本上的一道题目,在对数的第二节课时,同学已经能够算出答案,现在再重温“做过的”题目,让学生感受到掌握新公式,计算变得“简洁”,有了新的知识,认识问题的高度则不同,解决问题则变得更“便捷”;题(3)是指数运算,让学生复习一下指数的运算法则.在问题提出之前、解决问题过程之中、解决问题之后,教师设计的问题要及时引导学生进行反思、总结,使学生的解题能力和思维能力得到提升.

例2已知lg 6=a,lg 12=b,试用a,b表示lg 24.

变式已知log25=a,2b=3,试用a,b表示log1245.

设计意图例2是让学生了解到解决此类问题有两种方法:解法1是找出真数、底数之间的关系,此法需要学生有一定的观察力,有些难度;解法2是基本量法,发现真数最终可分解为2和3的幂的乘积形式,这样就找到了基本量是lg 2和lg 3,这样lg 24就能轻松求得.此法具有一定的普遍性.

4. 课堂小结

师:请同学们谈谈本节课的收获.(略)

三、教学反思

1.教师要理解数学,追求自然的数学教学

数学教学如果“不自然”,则会产生强加于人的效果,对学生数学学习的兴趣与内部动机都有不利影响.怎样使得数学教学自然呢?首要前提是教师要理解数学,理解数学就是要了解数学知识的背景,准确把握数学概念、定理、法则、公式等的逻辑意义,深刻领悟内容所反映的思想方法,把握知识之间的多元联系,能挖掘数学知识所蕴含的科学方法、理性精神和价值观资源和技术,善于区分核心知识和非核心知识等.我们要准确把握每块知识产生的背景,在教材中的地位、前后的联系、后续学习的必要性,其中蕴含的数学思想方法有哪些,这些数学思想方法在学习其他知识时是否可以利用、类比推广等.只有理解数学,我们才能准确地确定教学目标.

本节课,笔者认真研读教材,理解了对数的换底公式的由来、证明和应用.通过具体的数学小题,让学生领悟对数的换底公式的产生的必要性;从课本的例题出发,引导学生猜想并证明公式;精心设计例题,让学生理解公式的应用.

2.尊重学生的主体地位,让学生自然地感悟数学

“学之道在于悟,教之道在于度.”学生的独立思考是学生进行学习的必要条件.南京师大附中陶维林老师说过:“现在的数学教师教学最大的问题是什么?就是忘记了谁在学习.饭要让学生亲自吃,觉要让学生亲自睡,学习要让学生亲自学,老师绝不能代替.”本节课,为什么要学习换底公式?怎样证明换底公式?换底公式的推论是什么,有什么作用?这些问题的解决,都不是教师告知学生的,而是在教师精心设计的问题引导下,学生主动思考、主动发现,主动参与到问题的探究与解决过程中.在这过程中,学生自然地感悟到对数的换底公式的数学本质.