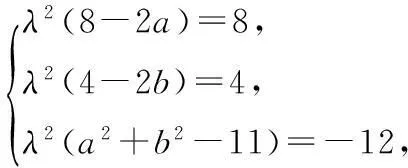高一数学测试
2016-07-07
○课外测试○
高一数学测试
一、填空题(本大题共14小题,每小题5分,共70分)
2.点M(-1,2,-3)关于原点的对称点是______.
3.已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0平行,则k=______.

6.两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上任意一点,则∆ABC面积的最小值是______.
8.已知l、m是两条不同的直线,α、β是两个不同的平面.下列命题:
①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;
②若l⊂α,l∥β,α∩β=m,则l∥m;
③若α∥β,l∥α,则l∥β;
④若l⊥α,m∥l,α∥β,则m⊥β.
其中真命题是______(写出所有真命题的序号).
9.从直线x-y+3=0上的点向圆x2+y2-4x-4y+7=0引切线,则切线长的最小值为______.


11.若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是______.
13.过点P(-4,0)的直线l与圆C:(x-1)2+y2=5相交于A,B两点,若点A恰好是线段PB的中点,则直线l的方程为______.
14.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与C有公共点,则k的最大值是______.
二、解答题(本大小题6小题,共90分.解答应写出必要的文字说明,证明过程或演算步骤)
15.(本小题满分14分)设锐角∆ABC的内角A、B、C的对边分别为a、b、c,且a=2bsinA.
(1)求B的大小;

(2)设直线l的方程为(a+1)x+y-2-a=0(a∈R),若直线l在两坐标轴上的截距相等,求直线l的方程.
17.(本小题满分16分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
(1)求证:PA∥面BDE;
(2)平面PAC⊥平面BDE.

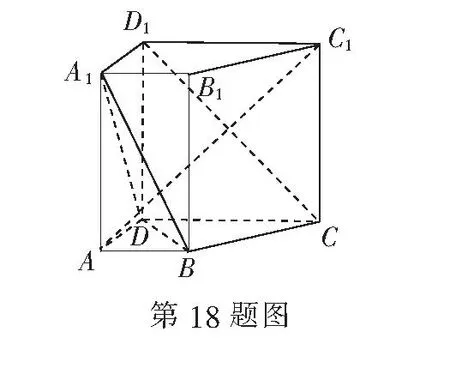
18.(本小题满分14分)如图所示,在四棱柱(侧棱垂直于底面的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
(1)求证D1C⊥AC1;
(2)设E是DC上一点,试确定点E的位置,使D1E∥平面A1BD,并说明理由.
19.(本小题满分16分)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.
20.(本小题满分16分)已知⊙O:x2+y2=1和点M(4,2).
(1)过点M向⊙O引切线l,求直线l的方程;
(2)求以点M为圆心,且被直线y=2x-1截得的弦长为4的⊙M的方程;
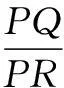
参考答案
一、填空题
1.120°;2.(1,-2,3);3.3或5;
11.(x-2)2+(y-1)2=1;12.6π;

二、解答题
15.(1)∵a=2bsinA,



由余弦定理b2=a2+c2-2accosB=7,

16.(1)当直线l的斜率不存在时,画出图象可知,直线x=1也符合题意.
当直线l的斜率k存在时,其方程可设为y-2=k(x-1),又设圆心到直线l的距离为d.
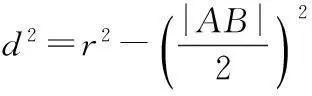
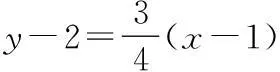
即3x-4y+5=0.所以直线l的方程为3x-4y+5=0和x=1.
(2)当直线l经过坐标原点时,该直线在两坐标轴上的截距都为0,此时2+a=0,解得a=-2,此时直线l的方程为x-y=0;

所以,l的方程为x-y=0或x+y-2=0.
17.(1)连结OE,如图所示.
∵O、E分别为AC、PC中点,∴OE∥PA.
∵OE⊂面BDE,PA⊄面BDE,
∴PA∥面BDE.
∵PO⊥面ABCD,∴PO⊥BD,
在正方形∆ABCD中,BD⊥AC,
∵PO∩AC=O,∴BD⊥面PAC,
又∵BD⊂面BDE,∴面PAC⊥面BDE.

18.(1)在直四棱柱ABCD-A1B1C1D1中,连结C1D.∵DC=DD1,
∴四边形DCC1D1是正方形,DC1⊥D1C.
又AD⊥DC,AD⊥DD1,DC∩DD1=D,
∴AD⊥平面DCC1D1,D1C⊂平面DCC1D1,
∴AD⊥D1C.
∵AD,DC1⊂平面ADC1,且AD∩DC1=D,
∴D1C⊥平面ADC1,
又AC1⊂平面ADC1,∴D1C⊥AC1.
(2)在DC上取一点E,连结AD1,AE,设AD1∩A1D=M,BD∩AE=N,连结MN.
∵平面AD1E∩平面A1BD=MN,要使D1E∥平面A1BD,须使MN∥D1E,又M是AD1的中点,
∴N是AE的中点,又易知∆ABN≌∆EDN,
∴AB=DE.即E是DC的中点.
综上所述,当E是DC的中点时,可使D1E∥平面A1BD.
19.(1)(x-1)2+(y-2)2=5-m,∴m<5.
(2)设M(x1,y1),N(x2,y2),
则x1=4-2y1,x2=4-2y2,
x1x2=16-8(y1+y2)+4y1y2.
∵OM⊥ON,∴x1x2+y1y2=0,
∴16-8(y1+y2)+5y1y2=0.
①

5y2-16y+m+8=0,


(3)以MN为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0,
即x2+y2-(x1+x2)x-(y1+y2)y=0,
20.(1)设切线l方程为y-2=k(x-4),易得



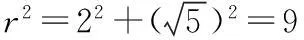
∴⊙M的方程为(x-4)2+(y-2)2=9.
(3)假设存在这样的点R(a,b),点P的坐标为(x,y),相应的定值为λ,根据题意,可得


即x2+y2-1=λ2(x2+y2-2ax-2by
+a2+b2).
(*)
又点P在圆上,∴(x-4)2+(y-2)2=9,
即x2+y2=8x+4y-11,代入(*),得
8x+4y-12=λ2[(8-2a)x+(4-2b)y+(a2+y2-11)].若系数对应相等,则等式恒成立,