常见简单线性规划问题
2016-07-07尚向阳
尚向阳
(陕西省周至县第一中学,710400)
常见简单线性规划问题
尚向阳
(陕西省周至县第一中学,710400)
高考数学对简单线性规划常考常新,解决好常见的线性规划问题是值得思考的.线性规划问题中目标函数的求解是线性规划问题的重点也是难点,对于目标函数的含义学生往往理解的不深不透,生搬硬套,导致思路混乱,解答出错.本文结合近几年高考,探讨归纳出高考常见的线性规划基本题型,提供解决相关的线性规划问题的解题策略,供大家参考.
一、基本类型——直线的截距型
例1(2015年广东高考题)若变量x,y满足约束条件
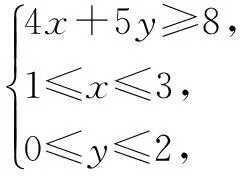
则z=3x+2y的最小值为()
解不等式所表示的可行域如图1所示.

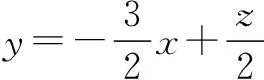
评注深刻地理解目标函数的含义,正确地将其转化为直线的纵截距是解决本题的关键.
二、直线的斜率型
例2(2015年全国高考题)若x,y满足约束条件

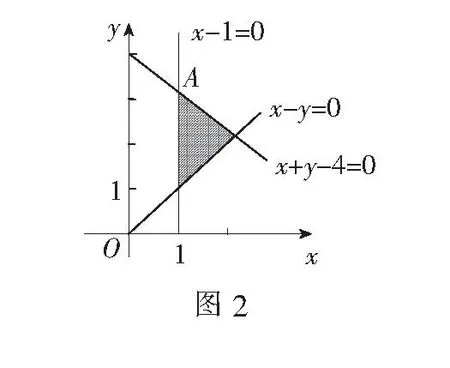
例3已知x、y满足约束条件

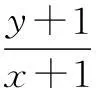
解作出可行域,如图3阴影部分所示.
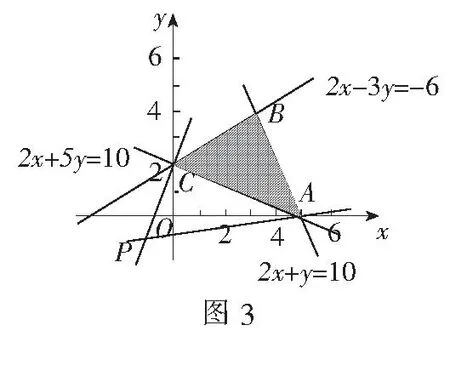
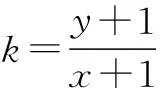
由图3,可知kPA最小,kPC最大,

三、平面内两点间的距离型(或距离的平方型)
例4已知实数x、y满足

则w=x2+y2-4x-4y+8的最值为______.
解目标函数w=x2+y2-4x-4y+8=(x-2)2+(y-2)2,其含义是点(2,2)与可行域内的点的距离的平方.由实数x、y所满足的不等式组作可行域如图4所示.
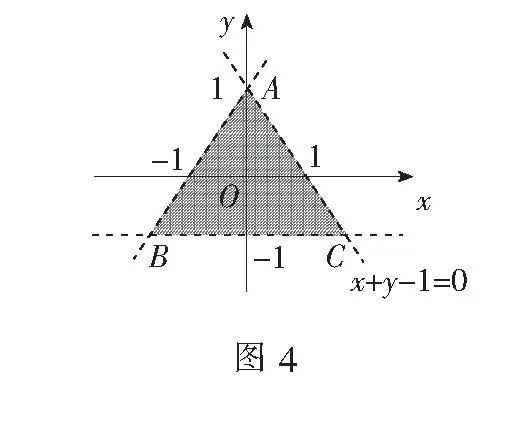
可行域为图中∆ABC内部(包括边界),易求得B(-2,-1).结合图形知,点(2,2)到点B的距离的平方为其到可行域内点的最大值,wmax=(-2-2)2+(-1-2)2=25;点(2,2)到直线x+y-1=0的距离为其到可行域内点的最小值,

评注将目标函数转化为两点间的距离或距离的平方是解决本类题的关键.
四、点到直线的距离型
例5已知实数x、y满足2x+y≥1,求u=x2+y2+4x-2y的最小值.
解目标函数u=x2+y2+4x-2y=(x+2)2+(y-1)2-5,其含义是点(-2,1)与可行域内的点的最小距离的平方减5.由实数x、y所满足的不等式组作可行域如图5所示(直线右上方):

点(-2,1)到可行域内的点的最小距离为其到直线2x+y=1的距离,由点到直线的距离公式,可求得
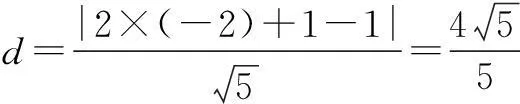

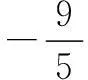
评注将目标函数转化为点到直线的距离或距离的平方是解决本类题的关键.
五、变换问题,研究目标函数
例6(2015年福建高考题)变量x,y满足约束条件
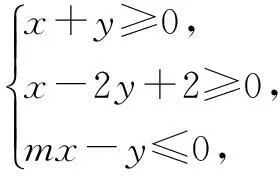
若z=2x-y的最大值为2,则实数m等于()
(A)-2(B)-1(C)1(D)2



评注结合参变量与目标函数进行转化变形是解决本类题的关键.
六、平面区域面积型
例7(2015年重庆高考题)若不等式组
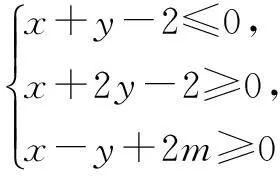


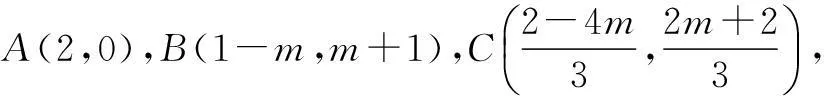
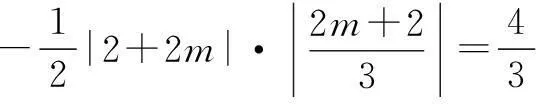
化简得(m+1)2=4,解得m=-3,或m=1.
检验知当m=-3时,已知不等式组不能表示一个三角形区域,故舍去;m=1符合题意;故答案选B.
评注由题意准确画出可行域,根据其形状来计算面积,基本方法是利用三角形面积,或切割为三角形,将目标函数转化为三角形的面积求解是解决本类题的关键.
七、以实际问题为背景,综合函数等知识类
例8(2015年陕西高考题)某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()
(A)12万元(B)16万元
(C)17万元(D)18万元
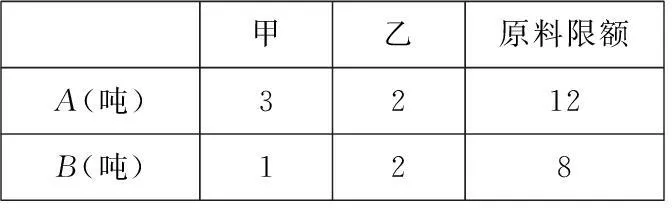
甲乙原料限额A(吨)3212B(吨)128
解设该企业每天生产甲、乙两种产品分别为x、y吨,则利润z=3x+4y,由题意得

其表示如图8阴影部分区域.

当直线3x+4y-z=0过点A(2,3)时,z取得最大值,所以zmax=3×2+4×3=18,故答案选D.
评注将实际问题转化为线性规划问题,解决的方法类似于线性规划问题.可依据题意写出线性约束条件,再画出可行域,寻找目标函数的最优解.常常以直线定边界,以特殊点判断区域,易发现线性目标函数的最优解往往在多边形可行域的顶点或边界处达到.
