一种改进的永磁交流伺服系统滑模控制器设计＊

2016-07-07郭小定

电气传动自动化 2016年2期

关键词：伺服系统鲁棒性神经网络

王　兴，郭小定，柏　达，范　婷

（湖南科技大学信息与电气工程学院，湖南湘潭411201）

一种改进的永磁交流伺服系统滑模控制器设计＊

王兴，郭小定，柏达，范婷

（湖南科技大学信息与电气工程学院，湖南湘潭411201）

摘要：针对传统整数阶PID伺服控制精度低、鲁棒性差等问题，结合滑模控制、分数阶理论、和神经网络参数整定技术各自的优点，提出了一种分数阶神经滑模控制的控制策略。首先对PMSM伺服系统的结构模型和数学模型进行了详细的阐述。然后利用滑模控制和等效控制理论设计了一种新的分数阶滑模控制器，提高了其综合性能。最后利用神经网络的强学习能力对分数阶滑模控制率参数进行了有效整定。实验结果表明，此分数阶神经滑模控制策略鲁棒性强、响应速度快、定位精度高，能有效消除抖振，具有良好的综合性能。

关键词：PMSM；伺服系统；滑模控制；分数阶；神经网络；鲁棒性

1　引言

随着微电子、计算机、电力半导体和电机制造技术的巨大进步，交流伺服控制技术日益成熟，应用日益广泛，特别是交流永磁伺服控制技术。目前伺服控制系统普遍采用的仍然是传统的PID控制方法，但由于永磁同步电动机（PMSM）自身具有一定的非线性、强耦合性和时变性等特点，且其伺服对象也存在较强的不确定性和非线性，加之系统运行时还会受到不同程度的干扰，因此，按照常规控制策略很难满足高性能永磁同步电动机伺服控制系统的控制要求，需要引进一种有效的控制技术使系统在复杂条件下仍能保持良好的伺服性能。

滑模变结构控制最突出的优点是系统一旦进入滑模运动状态，其对系统的扰动及参数变化就具有完全的鲁棒性，其对控制对象的模型精度要求不高，目前正被逐步引入到伺服电机控制系统中［1］，但滑模控制系统的抖震问题限制了其在实际工程中的广泛应用。针对传统滑模变结构控制系统中的抖振问题，把分数阶微积分理论引入到滑模控制方法中，并结合神经网络学习能力进行参数整定，有效消除抖振，同时提高其综合性能，提出了一种神经网络分数阶滑模控制策略。

2　交流伺服系统结构及数学模型分析

2．1伺服系统结构分析

基于永磁同步电机及其驱动器的交流伺服运动控制系统结构图如图1所示，图中驱动部分的伺服电机和驱动器外加编码器构成了通常所说的伺服系统，而伺服运动控制系统具有更加广泛的含义，除了驱动部分外，还包括操作软件、控制部分、检测元件、传动机构和机械本体，各部件协调完成特定的运动轨迹或工艺过程［2］。

图1　交流伺服系统控制结构图

在三环结构中，电流环和速度环为内环，位置环为外环。三环结构可以使伺服系统获得较好的动态跟踪性能和抗干扰性能。其中，电流环的作用是改造内环控制对象的传递函数，提高系统的快速性，及时抑制电流环内部的干扰，并限制最大电流，使系统具有足够大的加速扭矩，保障系统安全运行。速度环可以增强系统抗负载干扰的能力，抑制速度波动。位置环的作用是保证系统静态精度和动态跟踪性能，使整个伺服系统稳定高效运行。运动系统中一般是对伺服系统的速度环和位置环进行研究［2-3］，本文也是基于这两个环进行研究和设计。

2．2数学模型分析

PMSM的运动方程为：

由式（1）可得：

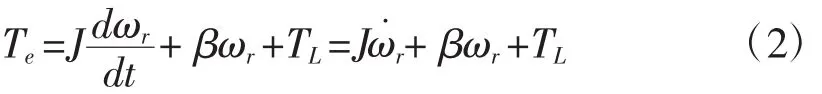
J为转动惯量（kg·m2），TL为负载转矩，β为粘滞摩擦系数，ωr为转子机械角速度，Te为电磁转矩（N·m）。

PMSM电磁转矩的方程为：

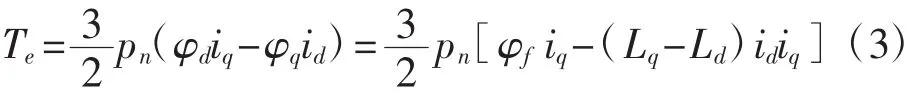
其中，φf为转子上的永磁体产生的磁势，φf＝ifLmd，φd、φq为dq轴的定子磁链，Ld、Lq为dq轴的定子电感。

通过应用矢量控制原理［2］，电磁转矩方程可以简化成：

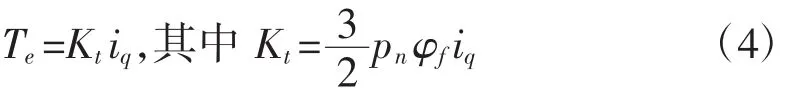
Kt为功率驱动电路的放大系数，iq为电流控制信号，pn为极对数。将式（4）代入式（2）可得：

如果考虑电机的参数变化，上式可表示为：

其中，Δa、Δb、Δc为系统的参数扰动值。控制器的设计目的是找到合适的控制率，使系统的输出角θ快速跟踪输入角θr。

3　分数阶滑模控制器的设计

分数阶滑模控制器的设计分为两步：滑模面的设计和滑模控制律的设计［4］。

分数阶切换函数选择为：

其中，0＜r＜1，c∈R+。

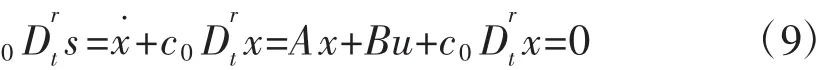
则等效控制ueq为：

为了保证滑模到达条件成立，设计切换控制如下：

滑模控制率由等效控制项和切换控制项组成，即：

4　神经网络整定开关增益

滑模控制器中的开关增益η对伺服系统的控制性能影响很大，抖振问题一直是滑模控制理论研究中难以解决的问题，究其原因主要是由于控制器的不连续切换项造成的，如果系统切换增益η太大，则系统的抖振变大，影响系统的控制精度；反之，如果切换增益η太小，则系统不能达到切换流型。因此，选择合适的方法，适当减小切换项增益，可有效消除抖振。本文采用一种学习能力强的神经网络算法来整定开关增益η。

神经网络输入输出算法为［9］：

hj为高斯函数，h＝［h1，h2，…hm，］T为高斯基函数的输出，x为网络输入向量，cj＝［cj1，cj2，…cjn，］T为第j个节点的中心矢量，bj为j节点的基宽度参数（大于零），W＊为理想网络权值，ε为网络的逼近误差（为很小的正实数），f为网络输出。

设网络的权值向量为W＝［w1，w2，…wm］T，则网络的辨识输出为：

定义神经网络的两个输入量：x1＝（sk），x2＝（sk）。选择神经网络的整定指标为：

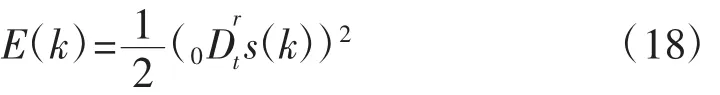
由式（9）可得：

根据梯度下降法，输出权值的网络学习迭代算法表示为：

式中ρ为学习速率，α为动量因子。

节点基宽参数的迭代算法为：

节点中心迭代算法为：

根据上述迭代算法［10］，可以整定出合适的开关切换增益系数η，从而使系统满足需求的控制性能。

图2　改进的PMSM滑模控制的伺服系统仿真模型

5　仿真结果与分析

为检验以上所设计的伺服控制策略的性能及其合理性，在永磁同步电机伺服系统结构基础上，以Matlab为仿真工具，在Simulink中搭建了仿真模型如图2所示，其中XSMC模块为分数阶神经滑模控制模块。然后，分别对系统的阶跃响应和正弦响应进行了仿真分析［11、12］。

设置永磁同步电机的主要参数为：Ld＝Lq＝8．0e-3H，pn＝2，J＝4．5e-4kg·m2，β＝1．0e-3N·m·s，定子电阻为2Ω，额定转速为1500r／min，额定功率为2kW，额定转矩为6．45N·m。滑模函数中取r＝0．5、c＝25，输入指令取θr（t）＝0．1sin（1．42πt），选择神经参数ρ＝0．6，α＝0．05，高斯函数参数初始值取网络权值的初始值为w＝［0．1，0．1，0．1，0．1，0．1］。

图3　电机速度的阶跃响应曲线

系统的速度阶跃响应曲线如图3所示，给定速度取100rad／s，从图3可以看出，改进的系统速度响应快，且超调量小，速度无明显波动，抗干扰能力强，具有较强的动态性能，符合系统的要求。接着在Matlab环境下，分别进行分数阶神经网络滑模控制器和传统整数阶PID（以一阶为例）控制策略进行仿真对比分析，以正弦响应曲线为例，仿真结果如图4和图5所示。

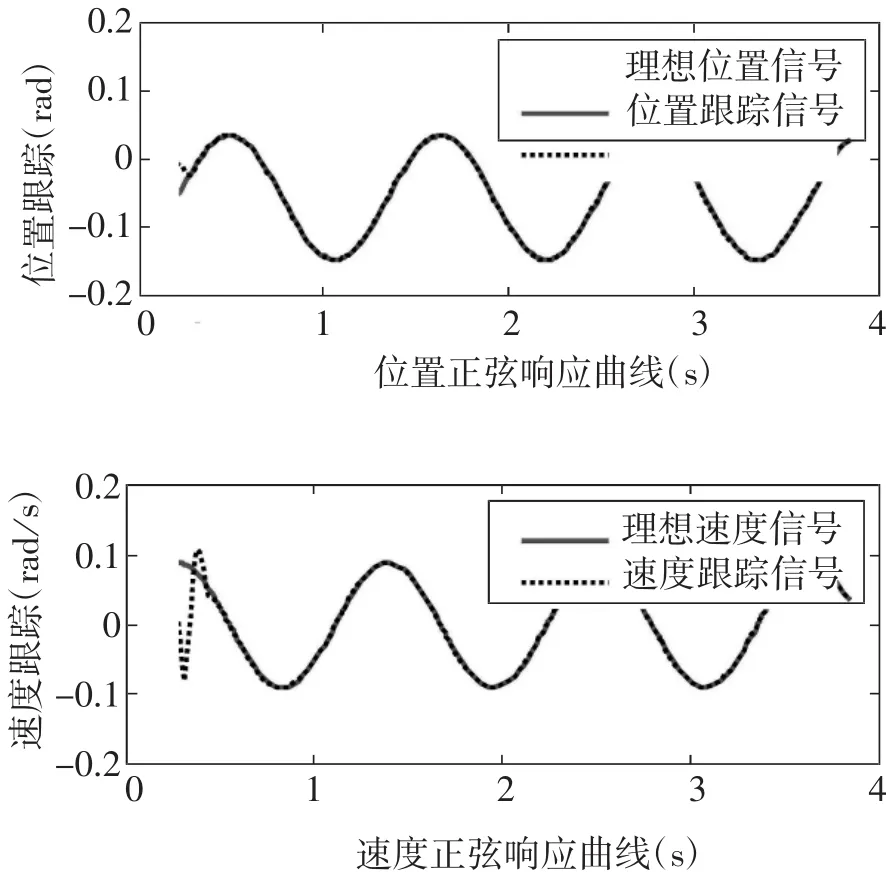
图4　分数阶神经滑模控制位置和速度正弦响应曲线

图5　传统PID控制的位置和速度正弦响应曲线

上图分别给出了分数阶神经网络滑模控制策略和传统PID控制策略（去掉图2模型中的XSMC模块）的仿真结果。从图4和图5可以看出，分数阶神经网络控制响应速度快，无论位置和速度响应时间都小于0．5s，甚至更快。它能以最快的加速度加速到额定速度，定位精度高，具有更好的正弦跟踪性能，对滑模参数能够进行整定，能够有效消减系统的抖振，系统运行稳定且鲁棒性强。而传统PID控制方法的响应时间相对较长，前期跟踪精度差，会出现明显偏差，这在如今高性能的伺服领域是不允许的。从上述几幅图中可以知道，分数阶神经滑模控制策略不但能有效削减系统自身抖振，还能达到比传统PID控制系统更好的综合控制性能，充分证明了其可行性。

6　结束语

本文针对传统伺服控制策略出现的缺点与不足，结合滑模控制、分数阶理论和神经网络参数整定技术各自的优点，完成了对PMSM交流伺服系统的一种改进型分数阶神经滑模控制器的设计。本文将分数阶理论应用到滑模控制系统中，采用等效控制的组合方式设计控制器的控制率，利用神经网络对其开环进行整定优化。永磁同步电机伺服系统仿真结果表明，本文所提出的改进型分数阶神经滑模控制策略不但鲁棒性强、抖振小，而且响应速度快、定位精度高，具有良好的综合性能，能够广泛应用于实际工程实践中。

参考文献：

［1］方斯琛，周波．滑模控制的永磁同步电机伺服系统一体化设计［J］．中国电机工程学报，2009，29（3）：96-101．

［2］金钰，胡佑德，等．伺服系统设计指导［M］．北京：北京理工大学出版社，2000．

［3］杨书生，钟宜生．永磁同步电机转速伺服系统鲁棒控制器设计［J］．中国电机工程学报，2009，29（3）：84-90．

［4］胡跃明．变结构控制理论与应用［M］．北京：科学出版社，2003．

［5］薛定宇，赵春娜．分数阶系统的分数阶PID控制器设计［J］．控制理论与应用，2007，24（5）：771-776．

［6］Zhang J J，Chen X L，Feng R P，et al．Design of variable structure controller based on friction adaptive compensation ［J］．Journal of Harbin Institute of Technology，2000，32 （4）：92-95．

［7］曾庆山，曹广益．分数阶线性系统的能观性研究［J］．系统工程与电子技术，2004，26（11）：1647-1650．

［8］曾庆山，曹广益，朱新坚．分数阶控制系统的仿真方法［J］．计算机仿真，2004，21（2）：84-86．

［9］LU Ying -wei，Sundararajan，Saratchandran．Performance evaluation of a sequential minimal radial basis function neural network learning algorithm［J］．IEEE Transactions on Neural Networks，1998，9（2）：308-318．

［10］刘治钢，王军政，赵江波．永磁同步电机神经网络自适应滑模控制器设计［J］．电机与控制学报，2009，13（2）：290-295．

［11］汪海波，周波，方斯琛．永磁同步电机调速系统的滑模控制［J］．电工技术学报，2009，29（9）：71-77．

［12］刘金琨．滑模变结构控制MATLAB仿真［J］．北京：清华大学出版社，2005．

Design of modified sliding-mode controller for permanent magnet AC servo system

WANG Xing，GUO Xiao-ding，BAI Da，FAN Ting

（School of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China）

Key words：PMSM；servo system；sliding mode control；fractional order；neural network；robustness

Abstract：In view of the traditional integer order PID servo control with low precision and poor robustness，combining with the respective advantages of the sliding mode control，the fractional theory and the neural network parameter setting，a neural sliding mode fractional order control strategy is proposed．Firstly，the full-digital fuzzy servo system structure model and mathematical model have been detailed，then the design of a new kind of fractional order sliding mode controller by using of the sliding mode control and equivalent control theory for improving the comprehensive performance is presented，and finally the parameters setting of the fractional order sliding mode control using the strong learning ability of the neural network is given．The experimental results show that this fractional order neural sliding mode control strategy enables the system of strong robustness，fast response and high positioning accuracy，and can effectively eliminate the chattering and makes the system good comprehensive performance．

中图分类号：TM351

文献标识码：A

文章编号：1005—7277（2016）02—0013—05

基金项目：＊国家自然科学基金资助项目（51577057）．

作者简介：