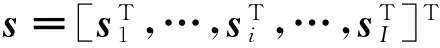基于优化投影矩阵的人脸识别技术研究
2016-07-07于爱华孙斌斌侯北平
于爱华,白 煌,孙斌斌,侯北平
(1.浙江工业大学 信息工程学院, 浙江 杭州 310023;2.浙江工业大学 浙江省信号处理重点实验室,浙江 杭州 310023;3.浙江科技学院 自动化及电气工程学院, 浙江 杭州 310023)
基于优化投影矩阵的人脸识别技术研究
于爱华1,2,3,白煌1,2,孙斌斌1,2,侯北平3
(1.浙江工业大学 信息工程学院, 浙江 杭州 310023;2.浙江工业大学 浙江省信号处理重点实验室,浙江 杭州 310023;3.浙江科技学院 自动化及电气工程学院, 浙江 杭州 310023)
摘要:针对大数据背景下人脸识别技术存在的问题,提出一种基于压缩感知的人脸识别技术架构.系统首先利用人脸训练样本优化设计投影矩阵,然后利用优化的投影矩阵进行人脸图像的压缩感知,利用同伦算法进行快速稀疏表示分类.这样人脸识别系统一方面避免大数据传输和存储压力,另一方面可以有效保证系统识别率,实验仿真证实了研究工作的有效性.
关键词:人脸识别;压缩感知;投影矩阵;同伦算法
人脸识别技术作为机器视觉和图像处理技术的重要研究方向之一,越来越受到学术界的高度关注[1-4].随着数字技术应用的不断深入,大数据背景下人脸识别技术对图像信息采集、传输、存储和处理等硬件设备提出越来越高要求.传统的解决方案是先对信号压缩,如基于离散余弦变换的JPEG标准[5]和基于小波变换的JPEG2000标准[6]等.它利用图像数据像素点间的相关性进行压缩,丢弃大部分冗余信息以得到压缩数据用于传输,后台接收端重建图像,提取图像特征用于身份识别.特征提取常用的方法有主成分分析(Principle components analysis,PCA)[7]、线性鉴别分析(Linear discriminant analysis,LDA)[8]等.PCA是寻找特征主要方向,其算法实现简单,但并没有考虑分类特点.LDA利用训练样本信息,使得类别内的点距离越近越好(集中),类别间的点越远越好,这样有利于分类.LDA降维的特征维度比类别的个数小,特征太少不利于分类.对图像进行识别分类的算法包括K最邻近分类算法(K-nearestNeighbor,KNN)[9]、支持向量机(Support vector machine,SVM)[10]、基于稀疏表示的分类器(Sparse representation based classifier,SRC)[11]以及符合图像物理特性的基于非负稀疏表示的分类器(Non-negative sparse representation based classifier,NNSRC)[12]以及神经网络[13-14]等.KNN不需要训练算法简单,但是效果一般.SVM和神经网络训练,识别率较高,但是要求有足够训练样本,且训练时间很长,容易陷入局部最优.SRC和NNSRC是通过稀疏表示分类,对遮掩有较好的识别效果,其识别过程较长,NNSRC增加了稀疏系数非负的约束,有较好的物理意义,但是其稀疏表示残余差较大,容易误判.
针对传统识别技术存在的问题,既然不需要图像中冗余信息,那么是否可以研究一种技术直接对图像信号进行压缩采样(特征提取),避免高速采样和丢弃信息过程造成的资源浪费,压缩感知(Compressed sensing,CS)理论就是一种试图完成这一目标的新兴理论[15-18],该理论一经提出就受到学术界的广泛关注.本算法的研究目标是利用压缩感知算法直接对图像进行特征提取,并利用投影矩阵优化技术,通过调整互相关性因子,使得同类测量数据互相关性提高,不同类别互相关性降低,来提高系统的识别率.
1压缩感知理论模型
对于一个输入的高维信号,x∈RN×1将其在矩阵Φ线性投影得到投影值,y过程为
y=Φx∈RM×1
(1)
其中Φ∈RM×N称为投影矩阵.CS理论研究的就是当M≪N对于给定的投影值y和投影矩阵Φ,如何求解原高维信号x.显然,式(1)为一个欠定问题,即方程个数少于未知数个数,存在无数多个解.因此,在求解过程中还需要对x加以限制.稀疏性约束就是CS理论中的一个关键因素,这个条件要求信号x可由L个基向量{ψl}线性表示为

(2)
其中:Ψ∈RN×L为字典(矩阵);s为一个大部分元素为零的稀疏向量,如果s含有K个非零元素,则x称为在Ψ下K稀疏.
将式(2)代入式(1)得
y=Φx=ΦΨsDs,‖s‖0≤K
(3)
其中D∈RM×L称为等效字典.
2基于CS的人脸识别系统
2.1压缩感知分类器的结构
基于压缩感知的分类器(Compressedsensingbasedclassifier,CSC),流程如图1所示.

图1基于压缩感知的识别流程图
Fig.1FR based on CS flowchart
当M≪N时,y数据量远少于x,这大大减小信道传输数据及后台存储、处理数据的压力.但是实际应用中,投影矩阵Φ对图像重建与识别效果影响较大,因此投影矩阵优化设计也是研究的主要内容之一.对于CS系统,投影矩阵的作用一方面是对输入信号的压缩,另一方面也是对信号的特征提取过程,经过优化设计的投影矩阵可大大提高信号识别分类及恢复的精度[17-18].
2.2基于CS人脸识别分类器的模型
假设一个人脸库中存储有L个人的脸部样本,其中每个人又都有许多不同角度、不同表情、不同光照的样本,每个样本的尺寸均相同.对每个人随机选中其Q个不同的样本,每个样本图像按照同样的排列规则形成一个列向量并分别做l2范数归一化处理,尺寸设为N×1,作为字典库中的一个原子,这样形成字典库Ψ=[Ψ1,Ψ2,…,Ψi,…,ΨI]={ψl}∈RN×L对任意的1≤i≤I字典子块Ψi∈RN×Q,是第i个人的样本集合,易见L=IQ.对1≤l≤L,ψl∈RN×1且‖ψl‖2=1是字典的一个列向量,即原子.
对于任意输入的测试样本,首先调整大小并按照上述排列图像的规则将其形成一个N×1的列向量x,则x在字典库Ψ下的表示方程为
x=Ψs+ε
(4)
其中ε∈RN×1为误差.研究的基于CS的人脸识别,将测试样本x进行压缩投影得到投影信号y∈RM×1(M y=Φx=ΦΨs+ΦεDs+e (5) 其中:Φ∈RM×N为设计好的具有一定性质的投影矩阵;D=ΦΨ∈RM×L为等效字典;e=Φε∈RM×1为投影域误差.CS理论要求信号x在字典Ψ下可稀疏表示,即s中含有很多的零元素,才可以从测量值y中精确地重构x.对于研究的人脸识别系统,字典库由I个不同人的样本组成,因此在重构s时利用块稀疏的性质. y=Φ(Ψ1s1+…+ψisi+…+ψIsI)+e (6) 对于所有s选取情况,要求非零元素只能存在于某一个si中,而其他部分均为零值.基于上述讨论,将式(6)拆解为 (7) 这个问题本身是一个NP-hard问题,在多项式时间内难以求解.可以通过贪婪算法如正交匹配追踪(OMP),和迭代收缩方法近似求得.在满足RIP条件下l0范数优化问题可以等价为l1范数优化问题.定义 Di=ΦΨi∈RM×Q (8) 这是一个凸优化问题可以有很多算法来解决如凸松弛类算法,迭代阈值法,Bregman迭代算法等.但是,这些算法复杂度高,这里使用同伦算法[19].该优化算法为 (9) 其中W为一个对角线上为λ的正对角矩阵. 求解这样一个同伦问题,即 (10) u (11) 第一步根据人脸样本,按照一定要求构造字典库Ψ=[Ψ1,…,Ψi,…,ΨI],将测试图像x0预处理形成列向量x. 第二步根据Ψ设计投影矩阵Φ. 3投影矩阵优化设计 延用前文记号,字典子块Ψi∈RN×Q,字典库Ψ=[Ψ1…,Ψi,…,ΨI]∈RN×L,等效字典为 D=ΦΨ=[D1,…,Di,…,DI]∈RM×L (12) 其中:投影矩阵Φ∈RM×N;Di=ΦΨi∈RM×Q. 学界关于CS系统中投影矩阵优化的研究已经取得许多理论成果[20-23],大体来看,这些成果的思路基本为 (13) 其中:‖·‖F定义为Frobenius范数;G为等效字典D的Gram矩阵;对于给定的字典Ψ,G只与投影矩阵Φ有关;Gt为一个目标Gram矩阵.式(13)的目的就是通过设计投影矩阵使得等效字典对应的Gram矩阵逼近一个给定的具有一定性质的目标Gram矩阵. 近年来,Cleju的研究表明[23]:对于不能在字典下完全稀疏表示的信号,比如图像信号,如果通过设计投影矩阵Φ使得等效字典D具有字典Ψ类似的性质,那么这样的CS系统将具备非常好的性能,此时选取的目标Gram矩阵为Gt=ΨTΨGΨ.对于研究的人脸图像样本,其在字典Ψ下的稀疏表示方程如式(4),一般情况下ε都不会是全零向量,因此可以考虑将Gt作为目标Gram矩阵来设计投影矩阵Φ. 字典库Ψ由I个不同人的脸部样本组成,即使是同一个人的样本也会因为角度、表情和光照等方面的区别而使得相关性变差,即同一个子块Ψi中的原子两两之间内积较小.另一方面,对于不同的两个人,即不同的字典子块之间,我们希望原子两两之间的相关性应该尽可能的小.令 (14) 对目标Gram矩阵做改进,即 Gt=ΨTΨ+Δ (15) 其中修正矩阵Δ∈RL×L可表达为 对任意1≤i≤P,1≤j≤P,Δij的尺寸均与Ψij相同;1≤m≤L,1≤n≤L,{δmn}为Δ中对应位置的元素且 (16) 其中η为互相关性调整因子,它是一个大于零的小常数,称为修正常数.通过式(15)构造的Gt既减小不同字典子块原子间的相关性,对同一字典子块内原子间的相关性又有适当加强.需要说明的是,前文提到字典库的每个原子都进行了归一化处理,即任意1≤l≤L,‖ψl‖2=1,因此原子间内积最大为1,即GΨ的对角线元素.为了使更新的Gt物理意义更明确,我们强制Gt中元素值最大为1因此对于其对角线元素我们并不改变它们的大小,而非对角元素在修正之后也不允许其超过1要大于零,这就对修正常数η的选取有了一定的要求.由此,形成投影矩阵设计问题 (17) Gt由式(15)定义. 设字典Ψ的SVD分解式为 (18) (19) 由此可选取 (21) 其中V22为任意尺寸为M×M的正交矩阵. 由此可见:关于投影矩阵Φ的优化设计只与字典Ψ和修正常数η有关,因此对于固定的Ψ及η,系统只要线下求得Φ,无需对每个输入测试图像都进行投影矩阵设计步骤,而且式(21)是解析解结果,计算代价并不大.此外,该结果中还存在两个自由度U及V22,这为进一步提高系统性能提供了可能性. 4实验结果分析 通过实验仿真验证基于CS的人脸识别系统的性能以及投影矩阵优化对系统性能的改进情况.实验中所用到的人脸样本库包括ORL库、Yale库、Yale-EXTENDED库(记为Yale-E)以及CMUPIE库(记为PIE). 仿真中对每个人脸库分别构造字典Ψ∈RN×L,其中对i=1,2,…,I,每个字典子块Ψi∈RN×Q,通过字典设计投影矩阵Φ∈RM×N.对每个库中的每个人脸样本均按照32×32的尺寸进行预处理并将其分别形成1 024×1的列向量,即N=1 024.对ORL库中40个人,每人随机选取5个脸部样本共200个原子组成字典库,此时P=40,Q=5;对Yale库15个不同人,每人随机选取8个脸部样本共120个原子组成字典库,此时P=15,Q=8;对Yale-E库38个不同人,每人随机50个脸部样本共1 900个原子组成字典库,此时P=38,Q=50;对PIE库68个不同的人,每人40个脸部样本共2 720个原子组成字典库,此时P=68,Q=40.对每个人脸库剩余样本,尽量随机选取5个样本作为测试信号,每次识别都重复进行10次实验,将10次实验结果取算术平均值作为最终结果进行识别率分析,同伦算法初始化参数λ=0.05. 4.1投影矩阵优化参数设置 针对上节投影矩阵优化设计中的几个参数进行测试.η值的选取:首先测试互相关性因子η对系统性能的影响.设定压缩投影值M=80,压缩率即为1 024/80,对不同的η取值,通优化算法设计投影矩阵Φ.图2描绘的是对于不同人脸库系统识别率随η变化曲线. 图2 系统识别率随η变化曲线Fig.2 System recognition rate vary with η 从图2中分析可知:对于Yale库和Yale-E库,保持系统原来互相关性就已经有很高的识别率,调整互相关性因子η对系统识别率没有明显改善作用;而对于ORL库和PIE库,适当选取的η确实提高了系统识别率.综合考虑,在后续仿真中固定修正常数η=0.03,对于这4人脸库而言均可取得较好的识别效果. 从CS理论分析可知:当压缩投影值M较大时,系统重建图像的精度也相对更高,但是相应的此时信道传输数据及后台处理数据的压力也越大.因此对于不同的应用场景,我们要权衡利弊.这部分主要验证M值的选取对系统识别率的影响,对于不同的M取值,通过优化算法设计投影矩阵Φ,图3描绘的是对于不同人脸库系统识别率随M变化曲线. 图3 系统识别率随M变化曲线Fig.3 System recognition vary with M 从图3中分析可知:系统识别率并非随着压缩投影值M单调变化.不同M值,Yale库识别率基本不变,由文献[25]可知:识别误差受其人脸类总数,类间最小距离,噪声误差影响,Yale库种类较小,类内变化也不大,所以当M=26时候,在很高压缩率下其识别率就已经较高;对于ORL库和Yale-E库,当M=80时系统识别率稳定在一个比较理想的位置;而PIE库虽然识别率不是随着M值单调增大,但整体上依旧还有上升的趋势.考虑到有效性问题,后续仿真中固定M=80,即压缩率为1 024/80. 4.2CSC性能测试 将测试信号按照上述设计好的投影矩阵进行投影压缩,再对投影值进行识别分类,分类方法分别采用KNN,SVM,NNSRC以及CSC,对4人脸库的识别率统计如表1所示. 表1 不同分类器识别率比较 由表1可见:对于ORL,Yale和Yale-E这3人脸库,CSC均得到最大的系统识别率,但应用于PIE库时,效果略差于NNSRC系统. 4.3投影矩阵优化算法性能测试 将测试信号按照PCA,压缩,随机采样,无压缩4种方式稀疏表示分类识别,对4人脸库的识别率统计如表2所示. 表2 不同压缩方法识别率比较 由表2数据表明:投影矩阵设计方法相对于随机采样及PCA在系统识别率上均达到最大值,尤其是对Yale库和PIE库的改善情况;但是相对于无压缩的情形,PIE库识别率依旧较低.M值的选取部分仿真预示,对PIE库系统识别率随M增加还有改善的趋势,因此尝试继续增大M,对PIE库系统识别率变化曲线如图4所示. 图4 对PIE库系统识别率随M变化曲线Fig.4 The recognition rate of PIE dataset vary with M 由图4可见:对PIE人脸库,当M值取到120时,系统识别率已经超过表2中无压缩的情形,而当M=240,系统识别率更是达到了98.24%,此时压缩率为1 024/240. 4.4图像重建效果测试 σmse‖ 信号重建性能采用峰值信噪比(Peaksignaltonoiseratio,PSNR)来衡量,定义为 σpsnr 其中r=8为每个像素点的编码比特数.图5描绘了σpsnr随着压缩投影值M的变化曲线. 图5 σpsnr随M变化曲线Fig.5 σpsnrvary with M 图5中每个人脸库σpsnr随M的变化趋势与图3中系统识别率的趋势基本吻合,均不随M值单调增大,但总体趋势是在上升. 5结论 以优化投影矩阵为基础,提出了基于压缩感知的人脸识别技术框架,系统首先根据训练样本的互相关矩阵,优化设计投影矩阵,然后对输入信号进行投影压缩,最后利用基于l1范数的同伦快速算法进行稀疏表示分类;通过对参数η优化,进一步提高识别率,对4个人脸库仿真结果证实在少量测量数据下,系统仍然保证有较高的识别精度并且有较好的重建效果. 参考文献: [1]ZHAO W Y, CHELLAPPA R., PHILLIP S P J,et al. Face recognition: a literature survey[J]. ACM computer surveys,2003,35(4):399-458. [2]LIU C J, WECHSLER H. Gabor feature based classification using the enhanced fisher linear discriminate model for face recognition[J]. IEEE transactions on neural networks,2002,11(4):467-476. [3]CHEN W L, ER M J, WU S Q. PCA and LDA in DCT domain[J].Pattern recognition letters,2005,26(15):2474-2482. [4]郑博,毛剑飞,梁荣华.基于纹理权重的AAM人脸特征点检测方法[J].浙江工业大学学报,2012,40(6):661-665. [5]WALLACE G K. The JPEG still picture compression standard[J].IEEE transactions on consumer electronics,1992,38(1):153-165. [6]TAUBMAN D S, MARCELLIN M W. JPEG2000: image compression fundamentals, standards and practice[M]. Berlin, German:Springer,2002. [7]TURK M, PENTLAND A. Eigen faces for recognition[J]. Cognitive neuroscience,1991,3(1):72-86. [8]SWETS D L, WENG J. Using discriminate eigen features for image retrieval[J]. IEEE transactions on pattern analysis and machine intelligence,1996,18(8):831-836, [9]WONG M, LANE T, A kth nearest neighbor clustering procedure[J]. Royal statistical society, series B, methodological,1983,45(3):362-368. [10]CORTES C, VAPNIC V. Support vector networks[J]. Machine learning,1995,20(1):1-25. [11]WRIGHT J, YANG A Y, GANESH A. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence,2009,31(2):210-227. [12]GAO Y, WANG X S,CHENG Y H. Dimensionality reduction of hyper spectral data using non-negative scarcity graph[J]. Electronics and information technology,2013,35(5):1177-1184. [13]吕刚,郝平.基于神经网络的数字验证码识别研究[J].浙江工业大学学报,2010,38(4):433-436. [14]朱海涛,徐建明,何德峰,等.基于最小均方delta规则的神经网络工件识别[J].浙江工业大学学报,2014,42(2):219-236. [15]CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE transactions on information theory,2006,52(2):489-509. [16]DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory,2006,52(4):1289-1306. [17]CANDES E J, TAO T. Near optimal signal recovery from random projection: universal encoding strategies[J]. IEEE transactions on information theory,2006,52(12):5406-5426. [18]CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE transactions on signal processing,2008,25(2):21-30. [19]ASIF M S,ROMBERG J. Sparse signal recovery for streaming signals using L1-homotopy[J]. IEEE transactions on signal processing,2013,46(7):3401-3413. [20]ZELNIK M L, ROSENBLUM K,ELDAR Y C. Sensing matrix optimization for block-sparse decoding[J]. IEEE transactions on signal processing,2011,59(9):4300-4312. [21]ABOLGHASEMI V, FERDOWSI S, SANEI S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing[J]. Transactions on signal processing,2012,92(4):999-1009. [22]LI G., ZHU Z H, YANG D H. On projection matrix optimization for compressive sensing systems[J]. IEEE transactions on signal processing,2013,61(11):2887-2898. [23]CLEJU N. Optimized projections for compressed sensing via rank-constrained nearest correlation matrix[J]. Applied and computational harmonic analysis,2014,36(3):495-507. [24]YU A H, ZHU Z H, BAI H, IIAN Q R,et al. Multi-objects classification via optimized compressive sensing projection[C]//2013 9th International Conference on Information, Communications and Signal Processing. Taiwan:IEEE,2013:1430-1434. [25]HORN R A,JOHNSON C R. Matrix analysis 2nd edition[M]. London, UK:Cambridge University Press,2012. (责任编辑:刘岩) Research on the face recognition technology based on optimized projection matrix YU Aihua1,2,3, BAI Huang1,2, SUN Binbin1,2, HOU Beiping3 (1.College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China;2.Zhejiang Key Laboratory for Signal Processing, Zhejiang University of Technology, Hangzhou 310023, China;3.School of Automation and Electrical Engineering, Zhejiang University of Science and Technology, Hangzhou 310023, China) Abstract:To solve the face recognition (FR) problem existed under the background of big data, a new kind of FR technology based on compressed sensing (CS) is proposed in this paper. Firstly, the projection matrix is optimized using the face train samples. Then, the optimized projection matrix are used on the face images based on compressed sensing and the homotopy algorithm is used in the compressed sparse representation classification. With these modifications, the new FR technology can avoid large data transmission and storage pressure. On the other hand, the system recognition rate can be guaranteed. The simulation experiments show that the proposed method is valid. Keywords:face recognition; compressed sensing; projection matrix; homotopy algorithm 收稿日期:2015-11-13 基金项目:国家自然科学基金资助项目(61273195,61304124,61413262,61503339);浙江省自然科学基金资助项目(LY13F010009,LQ14F030008);浙江省教育厅项目(Y201430687) 作者简介:于爱华(1975—),男,江苏海安人,博士研究生,主要从事数字信号处理研究,E-mail:yuaihua_seu@163.com. 中图分类号:TP391 文献标志码:A 文章编号:1006-4303(2016)04-0392-07