基于统一强度理论的套管全管壁屈服挤毁压力

林元华，邓宽海，孙永兴，曾德智（.西南石油大学油气藏地质及开发工程国家重点实验室；.西南石油大学石油管工程重点实验室）



基于统一强度理论的套管全管壁屈服挤毁压力

林元华1，邓宽海1，孙永兴2，曾德智2
（1.西南石油大学油气藏地质及开发工程国家重点实验室；2.西南石油大学石油管工程重点实验室）

摘要：在充分考虑套管拉压强度差、中间主应力、材料硬化、屈强比对套管全壁屈服挤毁压力影响的基础上，根据统一强度理论推导均匀外压下套管全壁屈服挤毁压力的统一算法。该方法适合于计算具有拉压强度差效应和中间主应力效应的套管挤毁强度；建立了VON MISES、TRESCA、GM、双剪屈服4种典型屈服准则下的全壁屈服挤毁公式，其中双剪屈服准则下计算公式的计算值最大，可作为全壁屈服挤毁压力设计的上限，TRESCA屈服准则下计算公式的计算值最小，可作为全壁屈服挤毁压力设计的下限。数据计算对比表明，新全壁屈服挤毁公式的计算值比其他公式更接近实验值。图6表1参31

关键词：统一强度理论；套管挤毁；全壁屈服；挤毁压力；拉压强度差；中间主应力

0 引言

近年来，随着石油和天然气勘探开发的不断深入，深井、超深井及钻遇膏岩、盐岩、页岩、软泥岩等塑性地层的井数量也不断增加[1-2]，使得石油套管的服役环境变得非常恶劣，尤其深井和超深井中的套管将受到更大的外挤压力，导致许多常规API套管不能完全满足深井和超深井的强度要求，严重制约深井和超深井钻井技术的发展及钻进深度的延伸[3]。

为满足深井和超深井对套管强度的要求，相继研制出了许多厚壁、非API及高抗挤套管[4-6]，与常规API套管相比，它们具有更高的抗挤毁性能[7]。尽管如此，近几年仍有关于高强度套管在深井和超深井中挤毁失效的相关报道[8]。因此，正确合理地预测和设计套管（尤其高抗挤套管）挤毁强度是确保油气安全开采的关键。

为准确预测并设计套管挤毁强度，国内外许多学者对均匀载荷下套管的屈服挤毁强度[9-14]进行了研究，并取得了一些重要成果[12, 14]，但大部分力学模型的设计原理是套管内壁屈服及失效。事实上，内壁开始屈服时套管并未完全破坏，且还有很大的抗挤余量[15-16]，若按此原理设计，会造成套管材料浪费或套管选择难的问题；其次，大部分力学模型[10-12]主要是基于VON MISES和TRESCA[17]屈服准则建立的，而没有充分考虑中间主应力效应和拉压强度差效应（即SD效应）对套管屈服挤毁压力的影响，仅适合于抗拉和抗压强度相等的材料；另外，研究还发现国际标准化组织（ISO）10400挤毁模型[14]中的全壁屈服挤毁压力公式（预测值远远低于套管真实的全壁屈服挤毁压力）并非真正的全壁屈服挤毁压力公式，导致其可能并不适合所有径厚比套管挤毁强度的计算[8, 16]。

为此，本文基于工程研究领域广泛应用的统一强度理论[18-20]，并考虑了SD效应、中间主应力效应、材料硬化、屈强比对套管全壁屈服挤毁压力的影响，推导出了套管全壁屈服挤毁压力计算公式。

1 套管全壁屈服挤毁压力公式

1.1 统一强度理论

统一强度理论[18-19]可以退化为现有的多种屈服准则和一系列新的屈服准则，它考虑了中间主应力和SD效应对材料强度的影响，可以灵活用于分析各种材料的塑性极限，其数学表达式为：

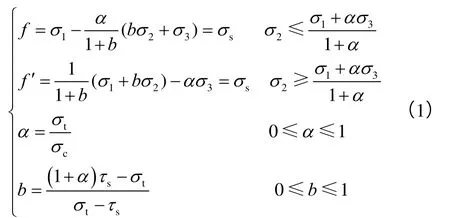
1.2 均匀外压作用下套管的弹性极限分析

套管在外界压力不断增加的情况下，应力分量不断增加，屈服首先在套管内壁发生，使得套管处于弹性极限状态。假设套管为一长厚壁圆筒，外表面受均匀外压作用，当外压较小时，厚壁圆筒处于弹性状态，根据拉梅公式[17]可以得到其应力分量：

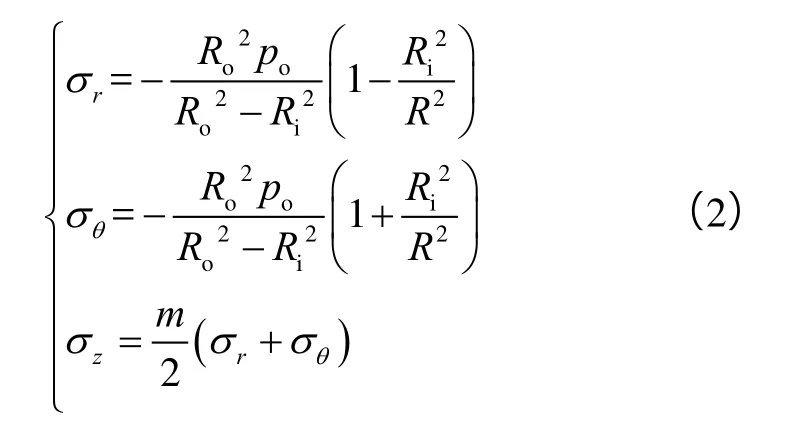
由于长厚壁圆筒属于轴对称平面应变问题，基于文献[21-22]对于平面应变弹塑性问题的研究，中间主应力在弹性区，m=2ν，在塑性区，m=1。当套管处于弹性极限状态（即内壁塑性区）时，由（2）式可得：

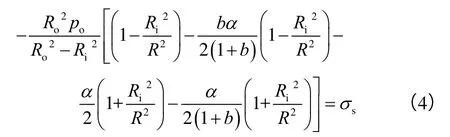
随着外压的增大，厚壁圆筒内壁首先发生屈服，且R=Ri，po=py，由（4）式可得其弹性极限压力py，也称为内壁屈服挤毁压力：

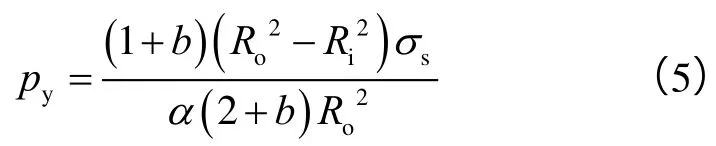
1.3 外压作用下套管的塑性极限分析

当po大于py时，在厚壁圆筒内壁附近出现塑性区，假设Rc为弹塑性分界面的半径，并且随着外压的继续增加，塑性区逐渐向外扩展，使得Ri≤R≤Rc区域成为塑性区，而Rc≤R≤Ro区域仍处于弹性区（见图1）。由于应力分量σθ、σr的轴对称性，塑性区与弹性区的分界面为圆柱面，在分界面上作用有界面压力pi，因此，分别将塑性区（内筒）和弹性区（外筒）按厚壁圆筒进行力学分析。在外筒（弹性区）的内壁和外壁分别作用有界面压力（pi）和外压（po），而内筒外壁作用有界面压力（pi）。

图1　套管弹塑性力学模型

在Ri≤R≤Rc的塑性区，由塑性力学平衡方程可得：

将（7）式代入（6）式：

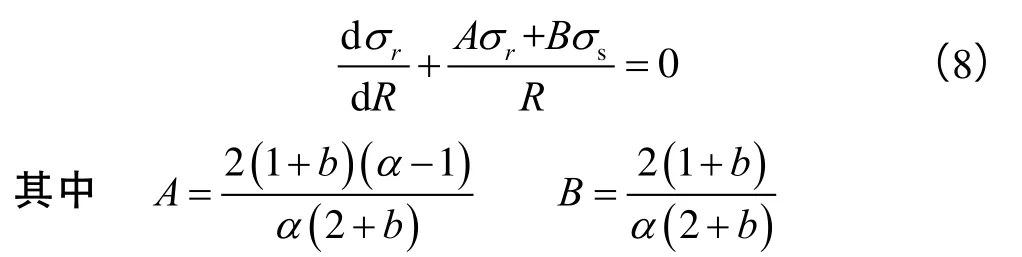
将边界条件（R=Ri，σr=0）代入（8）式求解可得：

将（9）式代入（7）式可得：

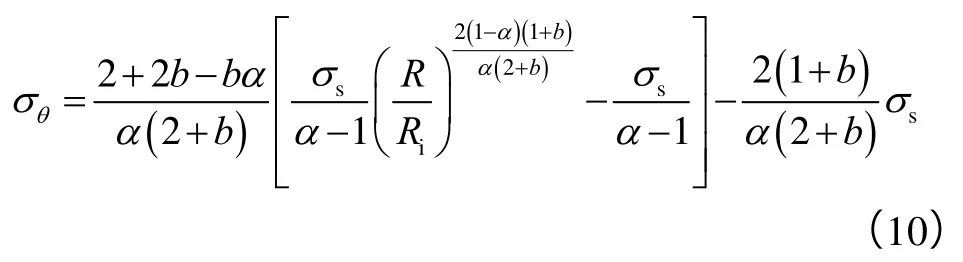
在弹性区，即Rc≤R≤Ro的外圆筒，根据拉梅公式可得其应力分量：

当R=Rc时，由（11）式可得外圆筒内壁的应力分量：

外圆筒内壁处于弹性极限状态，将m等于1代入（12）式，比较（12）式中的应力分量可得：

基于（13）式的等量关系，将（12）式代入（1）式求解可得界面压力：

根据应力分量的连续性，在弹性区与塑性区的分界面上（R=Rc），弹性区与塑性区的径向应力相等，由（9）式、（11）式、（14）式可得：

其中

随着压力的增加，塑性区不断扩大，当Rc=Ro时，套管整个截面进入塑性状态，根据（15）式可得套管全壁屈服挤毁压力：

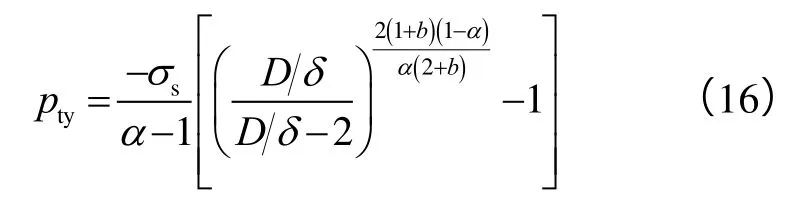
（16）式可以充分考虑材料的拉压比和中间主应力对套管全壁屈服挤毁压力的影响，因此，通过改变（16）式中α和b值可以计算不同套管（如API套管、高抗挤套管、非API套管）的全壁屈服挤毁压力，解决了ISO 10400挤毁模型中全壁屈服挤毁压力的计算问题及其未考虑SD效应和中间主应力效应对套管全壁屈服挤毁压力影响的问题，进一步改善了不同规格套管的强度设计，也为ISO 10400挤毁模型的进一步发展和完善提供了理论基础。

2 全壁屈服挤毁压力的分析与讨论

2.1 全壁屈服挤毁压力的分析

2.1.1 中间主应力效应对全壁屈服挤毁压力的影响

为了分析中间主应力效应对套管全壁屈服挤毁压力的影响规律，假设套管材料的抗拉屈服极限与抗压屈服极限相等，即α=1，对（16）式求极限可得：

基于（17）式可以分析中间主应力对套管全壁屈服挤毁压力的影响规律。分别取中间主应力对材料破坏的影响系数为0，0.25，0.50，0.75，以P110套管为例，分别计算该套管径厚比（D/δ=2Ro/(Ro-Ri)）为5～30时的全壁屈服挤毁压力与屈服强度之比，简称挤毁比（见图2）。

由图2可知，挤毁比随着中间主应力对材料破坏的影响系数的增加而增加，与文献得到的趋势基本相似[13]，且在所有的径厚比范围内，中间主应力对材料破坏的影响系数的大小对挤毁比的影响规律基本一致。由此可知，中间主应力对全壁屈服挤毁压力具有较大影响，故不容忽视。在套管强度设计时，合理考虑中间主应力的影响，可充分发挥套管材料的强度潜能。

2.1.2 SD效应对全壁屈服挤毁压力的影响

为了分析SD效应对套管全壁屈服挤毁压力的影响规律，假设b=1并带入（16）式可得：

图2　中间主应力对材料破坏的影响系数与挤毁比的关系

基于（18）式可分析SD效应对套管全壁屈服挤毁压力的影响规律，由于套管材料的抗拉强度与抗压强度之比一般在0.8左右[23]，故分别取拉压比为0.7，0.8，0.9，1.0。以P110套管为例，分别计算该套管在5≤D/δ≤30时的挤毁比（见图3）。

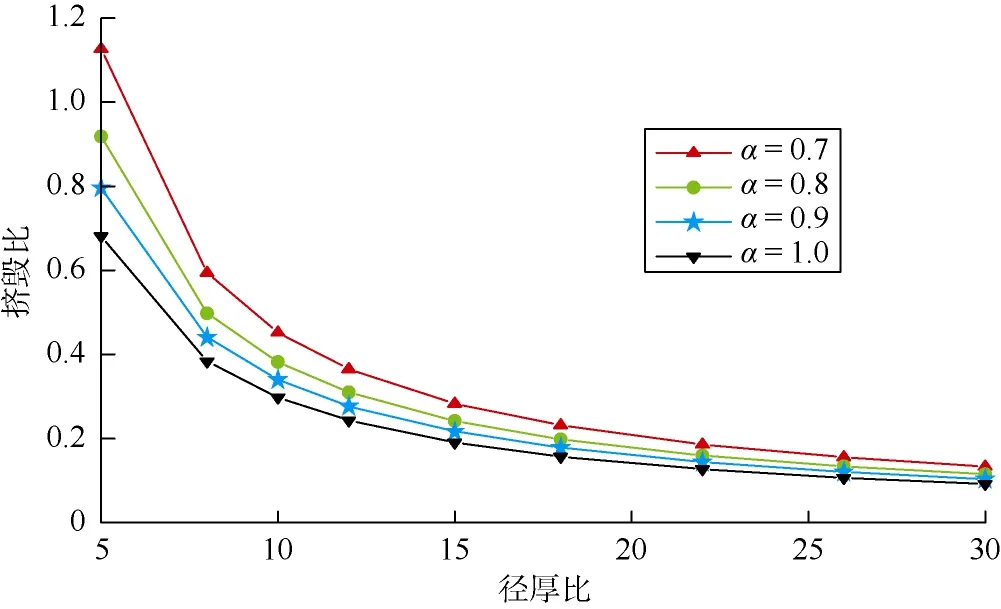
图3　SD效应与挤毁比的关系

由图3可知，挤毁比随着拉压比的增加而降低，即抗拉强度与抗压强度的差异越大，其挤毁比越大，且随着径厚比的增加，SD效应对挤毁比的影响程度逐渐降低，但总体上来看，SD效应对全壁屈服挤毁压力具有较大影响。因此，在套管强度设计时，合理考虑SD效应的影响，可以充分发挥套管材料的强度潜能，提高套管的挤毁性能。

2.1.3 不同屈服准则对全壁屈服挤毁压力的计算效果

在抗拉强度与抗压强度相等的极端情况下，统一强度理论可演变为多种重要的屈服准则，如VON MISES、TRESCA、GM[24-25]和双剪屈服等屈服准则，因此可通过改变（16）式中α和b的值获得多种计算套管全壁屈服挤毁压力的公式。

2.1.3.1 VON MISES屈服准则

2.1.3.2 TRESCA屈服准则

当α=1，b=0，统一强度理论退化为TRESCA屈服准则，由（16）式求极限可得该屈服准则对应的套管全壁屈服挤毁压力计算公式：

2.1.3.3 GM屈服准则

当α=1，b=2/5，统一强度理论退化为GM屈服准则，由（16）式求极限可得GM屈服准则对应的套管全壁屈服挤毁压力计算公式：

2.1.3.4 双剪屈服准则

当α=1，b=1，统一强度理论退化为双剪屈服准则，由（16）式求极限可得该屈服准则对应的套管全壁屈服挤毁压力计算公式：

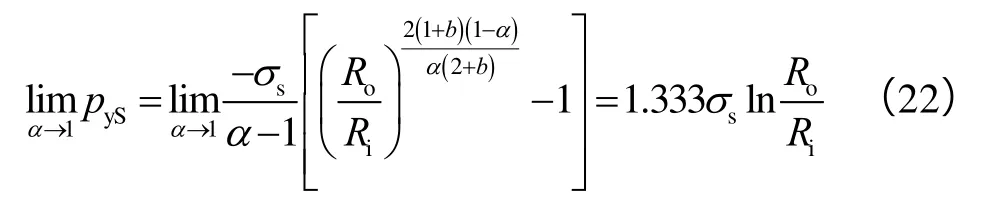
为了分析上述不同屈服准则对套管全壁屈服挤毁压力的计算效果，以N80和J55两种钢级的套管为例，分别采用不同屈服准则下的全壁屈服挤毁公式（即（19）式、（20）式、（21）式和（22）式）计算N80 和J55两种套管的全壁屈服挤毁压力，计算结果见图4、图5。

由图4、图5可知，套管全壁屈服挤毁压力随着径厚比的增加急剧降低。双剪屈服准则对应的全壁屈服挤毁公式计算值最大，TRESCA屈服准则对应的全壁屈服挤毁公式计算值最小，其余两种屈服准则对应的全壁屈服挤毁公式计算值基本相同。最大计算值（（22）式的计算值）与最小计算值（（20）式的计算值）的差异约30%，表明：屈服准则对套管全壁屈服挤毁压力具有显著的影响。因此，在抗拉强度与抗压强度相等的极端情况下，双剪屈服准则对应公式的计算值可作为全壁屈服挤毁压力设计的上限，TRESCA屈服准则对应公式的计算值可作为全壁屈服挤毁压力设计的下限，而VON MISES屈服准则和GM屈服准则对应公式的计算值可作为全壁屈服挤毁压力的平均值。

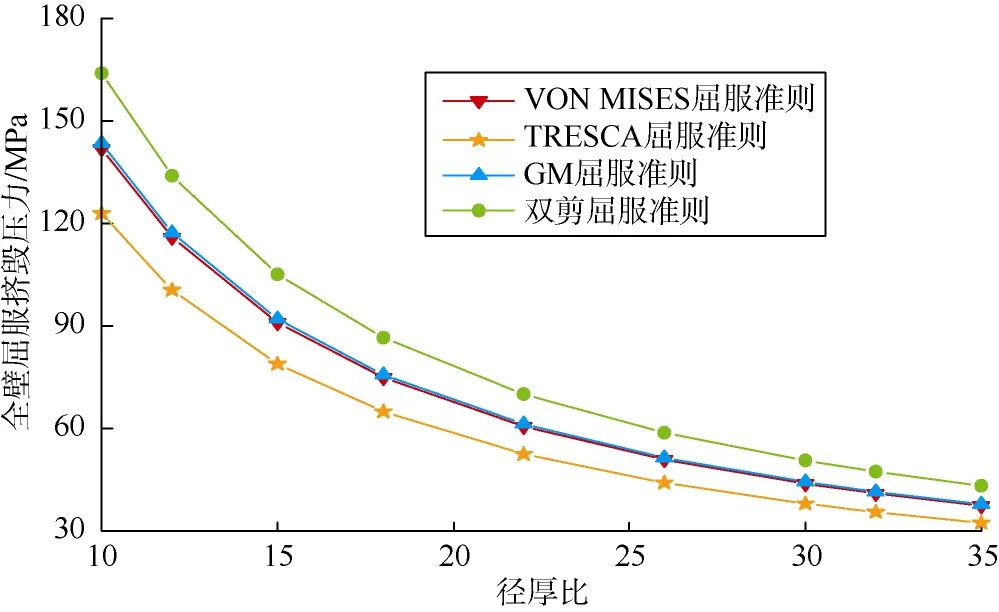
图4　N80套管全壁屈服挤毁压力

图5　J55套管全壁屈服挤毁压力

2.2 全壁屈服挤毁压力公式的讨论

由于套管从内壁屈服到外壁屈服要经历硬化和塑性流动两个阶段，采用屈服强度计算套管的全壁屈服挤毁压力不够完善，在塑性流动阶段需引入流动应力代替屈服强度来计算套管的全壁屈服挤毁压力。KLEVER[26]的研究结果表明：流动应力是介于屈服强度与抗拉强度之间的一个值，它考虑了材料硬化对套管全壁屈服挤毁压力的影响。大量学者针对不同金属管材给出了计算流动应力经验公式[27-29]：

为充分考虑应变硬化对套管挤毁强度的影响，本文根据材料的屈强比（对套管全壁屈服挤毁压力影响规律的研究[30]，给出了计算套管全壁屈服挤毁压力的公式：

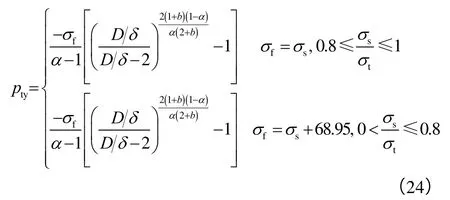
采用（24）式能准确合理地计算套管（尤其高抗挤套管）的全壁屈服挤毁压力，在保证材料安全的前提下，很大程度上改善了深井、超深井套管强度设计，为套管强度设计提供了重要参考和新思路。

对比内壁屈服与全壁屈服挤毁压力可知，当套管受到的外压等于内壁屈服挤毁压力时，只有套管内部开始屈服而发生局部塑性变形，但套管不会被挤毁，被称为内壁屈服挤毁设计，相反，套管还能承受更高的外压，直到套管受到的外压等于全壁屈服挤毁压力时，套管内壁到外壁均屈服而发生塑性变形，理论上套管会被该压力挤毁，被称为全壁屈服挤毁设计。套管内壁屈服和全壁屈服挤毁设计适用于只受到均匀内外压作用而不受到温度及温差影响的常规非酸性环境下的套管，尤其高抗挤套管。对于酸性环境，屈服失效准则已不适用，环境断裂是套管的主要失效模式，因此，对于酸性油气田，套管除满足屈服失效设计准则之外，还需满足断裂力学设计准则；对于温度较高且温差较大的井筒，需要考虑温度及温差产生的附加热应力对套管挤毁强度的影响。

最后，需要说明的是，本文推导的全壁屈服挤毁压力公式仅适用于均匀外压的情况，而针对非均匀外压的情况，需要先对套管受到的非均匀载荷进行简化并作相关假设，然后采用统一强度理论及弹塑性极限分析方法对非均匀外压下套管全壁屈服挤毁压力公式进行推导和求解。由于非均匀载荷对套管挤毁强度具有显著的影响，因此，有必要基于统一强度理论及相关分析方法开展非均匀载荷下套管全壁屈服挤毁压力的研究。

3 计算结果与实验值的对比

通过分析可知，双剪屈服准则对应公式的计算值可作为全壁屈服挤毁压力设计的上限，而API和ISO挤毁模型的预测结果较保守，尤其API挤毁模型，因此，本文采用双剪屈服准则所对应的全壁屈服挤毁公式代替ISO 10400挤毁模型中的全壁屈服挤毁公式，形成新的挤毁强度计算模型，并将新模型与API模型[12]、ISO 10400模型[14]的计算结果及实验值进行对比（见图6、表1）。9组典型测试数据源于文献[31]。

图6　3种模型套管挤毁强度计算值与实验值比较

表1　套管挤毁强度的实验值与模型计算值对比

由图6和表1可知，本文模型的计算结果与套管挤毁强度的实验值最接近，且计算值与实验值之间的误差均小于10%，而ISO和API模型计算结果均小于实验值，且其误差均大于10%，尤其API计算模型。由此验证了本文提出的全壁屈服挤毁公式的准确性和可靠性，可为套管挤毁强度的计算及设计提供重要参考。

4 结论

本文推导出的套管全壁屈服挤毁压力公式充分考虑了SD效应、中间主应力效应、材料硬化、屈强比对套管全壁屈服挤毁压力的影响，可用于计算存在拉压强度差和中间主应力效应的套管全壁屈服挤毁强度，从而解决了ISO 10400抗挤模型不能准确、合理计算套管全壁屈服挤毁压力的问题，弥补了ISO 10400挤毁模型不适合于所有径厚比套管挤毁强度计算的不足。

分析了SD效应和中间主应力效应对套管屈服挤毁压力的影响规律，给出了4种典型屈服准则下的套管全壁屈服挤毁压力计算公式，其中双剪屈服准则下的计算公式的计算值最大，可作为全壁屈服挤毁压力设计的上限，TRESCA屈服准则下的计算公式的计算值最小，可作为全壁屈服挤毁压力设计的下限，而VON MISES和GM屈服准则下的计算公式的计算值居中且十分接近，可作为全壁屈服挤毁压力设计的平均值。

本文模型计算的准确性得到了套管挤毁实验值的验证。

符号注释：

b——中间主应力对材料破坏的影响系数；D——套管外径，mm；f，f '——第二主应力取不同值时的主应力强度理论函数，MPa；m——塑性系数，无因次；pAPI——API模型的挤毁强度，MPa；pi——弹性区与塑性区之间的界面压力，MPa；pISO——ISO模型的挤毁强度，MPa；po——外界压力，MPa；ptest——实验的挤毁强度，MPa；pty——全壁屈服挤毁压力，MPa；py——内壁屈服挤毁压力，MPa；pyG——GM屈服准则对应的套管全壁屈服挤毁压力，MPa；pyL——VON MISES屈服准则对应的套管全壁屈服挤毁压力，MPa；pyS——双剪屈服准则对应的套管全壁屈服挤毁压力，MPa；pyT——TRESCA屈服准则对应的套管全壁屈服挤毁压力，MPa；R——套管任意位置处的半径，mm；Rc——弹塑性分界面的半径，mm；Ri，Ro——套管内、外径，mm；δ——套管壁厚，δ=Ro-Ri，mm；α——材料的拉压比；ν——泊松比；σ1，σ2，σ3——第1、第2、第3主应力，MPa；σc——材料的抗压强度，MPa；σf——流动应力，MPa；σs——材料的屈服应力，MPa；σt——材料的抗拉强度，MPa；σz，σθ，σr——轴向应力、环向应力、径向应力，MPa；τs——材料的剪切强度，MPa。

参考文献：

[1] 常德玉, 李根生, 沈忠厚, 等.深井超深井井底应力场[J].石油学报, 2011, 32(7): 697-703.CHANG Deyu, LI Gensheng, SHEN Zhonghou, et al.The stress field of bottom hole in deep and ultra-deep wells[J].Acta Petrolei Sinica, 2011, 32(7): 697-703.

[2] 温航, 陈勉, 金衍, 等.硬脆性泥页岩斜井段井壁稳定力化耦合研究[J].石油勘探与开发, 2014, 41(6): 748-754.WEN Hang, CHEN Mian, JIN Yan, et al.A chemo-mechanical coupling model of deviated borehole stability in hard brittle shale[J].Petroleum Exploration and Development, 2014, 41(6): 748-754.

[3] 张波, 管志川, 张琦, 等.高压气井环空压力预测与控制措施[J].石油勘探与开发, 2015, 42(4): 518-522.ZHANG Bo, GUAN Zhichuan, ZHANG Qi, et al.Prediction of sustained annular pressure and the pressure control measures for high pressure gas wells[J].Petroleum Exploration and Development, 2015, 42(4): 518-522.

[4] 王军, 毕宗岳, 韦奉, 等.国内SEW油套管开发现状[J].钢管, 2014, 43(4): 7-10.WANG Jun, BI Zongyue, WEI Feng, et al.Current situation of domestic R & D of SEW tubing/casing[J].Steel Pipe, 2014, 43(4): 7-10.

[5] 王少华, 王军, 张峰.BSG-80TT 高抗挤套管的研制[J].焊管, 2014, 37(5): 35-39.WANG Shaohua, WANG Jun, ZHANG Feng.R & D of BSG-80TT high collapse-resistance casing[J].Welded Pipe and Tube, 2014,37(5): 35-39.

[6] 严泽生, 高德利, 张传友, 等.一种新型高抗挤套管的研制[J].钢铁, 2004, 39(4): 35-38.YAN Zesheng, GAO Deli, ZHANG Chuanyou, et al.Research and development of new casing with high collapse strength[J].Iron and Steel, 2004, 39(4): 35-38.

[7] 王军, 田晓龙, 樊振兴, 等.SEW高抗挤套管抗外压挤毁性能研究[J].钢管, 2014, 43(2): 16-21.WANG Jun, TIAN Xiaolong, FAN Zhenxing, et al.Research on resistance properties against external collapse of SEW High collapse-resistant casing[J].Steel Pipe, 2014, 43(2): 16-21.

[8] LIN Y H, SUN Y X, SHI T H, et al.Equations to calculate collapse strength for high collapse casing[J].Journal of Pressure Vessel Technology, 2013, 135(4): 14-16.

[9] KLEVER F J, TAMANO T.A new OCTG strength equation for collapse under combined loads[J].SPE Drilling & Completion, 2006, 21(3): 164-179.

[10] SUN Y X, LIN Y H, WANG Z S, et al.A New OCTG strength equation for collapse under external load only[J].Journal of Pressure Vessel Technology, 2011, 133(1): 549-554.

[11] HAN J Z, SHI T H.Equations calculate collapse pressures for casing strings[J].Oil Gas Journal, 2001, 99(4): 44-47.

[12] America Petroleum Institute.Bulletin on formulars and calculations for casing, tubing, drill pipe and line properties[S].6th ed.Washington: America Petroleum Institute, 1994.

[13] 赵均海, 李艳, 张常光, 等.基于统一强度理论的石油套管柱抗挤强度[J].石油学报, 2013, 34(5): 969-976.ZHAO Junhai, LI Yan, ZHANG Changguang, et al.Collapsing strength for petroleum casing string based on unified strength theory[J].Acta Petrolei Sinica, 2013, 34(5): 969-976.

[14] International Organization for Standardization.Petroleum and natural gas industries-formulae and calculation for casing, tubing, drill pipe and line pipe properties[S].6th ed.Switzerland: International Organization for Standardization, 2007.

[15] 韩建增, 李中华, 张毅, 等.特厚壁套管抗挤强度计算及现场应用[J].天然气工业, 2003, 23(6): 77-79.HAN Jianzeng, LI Zhonghua, ZHANG Yi, et al.Collapsing strength calculation and on-site application of extra-heavy wall casing[J].Natural Gas Industry, 2003, 23(6): 77-79.

[16] 孙永兴, 林元华, 施太和, 等.套管全管壁屈服挤毁压力计算[J].石油钻探技术, 2011, 39(1): 48-51.SUN Yongxing, LIN Yuanhua, SHI Taihe, et al.Calculation of yield collapse pressures for casing through-wall[J].Petroleum Drilling Techniques, 2011, 39(1): 48-51.

[17] 徐芝纶.弹性力学[M].4版.北京: 高等教育出版社, 2006.XU Zhilun.Elasticity mechanics[M].4th ed.Beijing: Higher Education Press, 2006.

[18] YU M H.Unified strength theory and its applications[M].Berlin: Springer, 2004.

[19] YU M H.Advances in strength theories for materials under complex stress state in the 20th century[J].Applied Mechanics Reviews, 2002, 55(3): 169-218.

[20] 金乘武, 王立忠, 张永强.薄壁管道爆破压力的强度差异效应与强度准则影响[J].应用数学和力学, 2012, 33(11): 1266-1274.JIN Chengwu, WANG Lizhong, ZHANG Yongqiang.Strength differential effect and influence of strength criterion on burst pressure of thin-walled pipelines[J] Applied Mathematics and Mechanics, 2012, 33(11): 1266-1274.

[21] YU M H, YANG S Y, LIU C Y, et al.Unified plane-strain slip line field theory system[J].China Civil Engineering Journal, 1997, 30(2): 182-185.

[22] LEE Y K, GHOSH J.The significance of J3to the prediction of shear bands[J].International Journal of Plasticity, 1996, 12(9): 1179-1197.

[23] LAW M, BOWIE G.Prediction of failure strain and burst pressure in high yield-to-tensile strength ratio linepipe[J].International Journal of Pressure Vessels and Piping, 2007, 84(8): 487-492.

[24] 赵德文, 张雷, 章顺虎, 等.用GM屈服准则解析薄壁筒和球壳的极限载荷[J].东北大学学报(自然科学版), 2012, 33(4): 521-523, 532.ZHAO Dewen, ZHANG Lei, ZHANG Shunhu, et al.Limit load of thin-walled cylinder and spherical shell with GM yield criterion[J].Journal of Northeastern University (Natural Science), 2012, 33(4): 521-523, 532.

[25] 章顺虎, 高彩茹, 赵德文, 等.GM 准则解析受线性荷载简支圆板的极限载荷[J].计算力学学报, 2013, 30(2): 292-295.ZHANG Shunhu, GAO Cairu, ZHAO Dewen, et al.limit load analysis of simply supported circular plate under linearly distributed load with GM criterion[J].Chinese Journal of Computational Mechanics, 2013, 30(2): 292-295.

[26] KLEVER F J.Burst strength of corroded pipe: “Flow stress”revisited[R].SPE 7029-MS, 1992.

[27] ZHU X K, BRIAN N L.Influence of yield to tensile strength ratio on failure assessment of corroded pipeline[J].Journal of Pressure Vessel Technology, 2005, 127(4): 436-442.

[28] American National Standards Institute.Manual for determining the remaining strength of corroded pipelines: ASME Guide for gas transmission and distribution piping systems B31G[S].America: American Society of Mechanical Engineers, 1984.

[29] KIEFNER J F, VIETH P H.A modified criterion for evaluating the remaining strength of corroded pipe[R].Ohioan: Battelle Columbus Div., 1998.

[30] 孙永兴.油套管抗内压抗挤强度研究[D].成都: 西南石油大学, 2008.SUN Yongxing.Study on collapse strength and internal pressure strength of casing and tubing[D].Chengdu: Southwest Petroleum University, 2008.

[31] ASBILL W T, CRABTREE S, PAYNE M L.DEA-130 modernization of tubular collapse performance properties[R].San Antonio: Southwest Research Institute, 2002.

联系作者：邓宽海（1988-），男，四川内江人，现为西南石油大学博士研究生，主要从事油井管、油气钻井工艺方面的研究工作。地址：四川省成都市新都区，西南石油大学石油与天然气工程学院，邮政编码：610500。E-mail: dengkuanhai@163.com

（编辑 郭海莉）

Through-wall yield collapse pressure of casing based on unified strength theory

LIN Yuanhua1, DENG Kuanhai1, SUN Yongxing2, ZENG Dezhi2
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University), Chengdu 610500, China; 2.CNPC Key Lab for Tubular Goods Engineering (Southwest Petroleum University), Chengdu 610500, China)

Abstract：The unified algorithm of through-wall yield collapse pressure for casing with due consideration of strength differential (SD), yield-to-tensile strength ratio, material hardening and intermediate principal stress, which is suitable to calculate collapse strength of all casing has been obtained based on unified strength theory, and four classical through-wall yield collapse formulas of casing have been presented based on the L.Von Mises, TRESCA, GM and twin yield strength criterion.The calculated value is maximum based on the twin yield strength criterion, which can be used as upper limit of through-wall yield collapse pressure, and the calculated value is minimum based on the TRESCA strength criterion, which can be used as lower limit of through-wall yield collapse pressure in the design process.Numerical and experimental comparisons show that the equation proposed by this paper is much closer to the collapse testing values than that of other equations.

Key words：unified strength theory; casing collapse; through-wall yield; collapse pressure; strength differential; intermediate principal stress

中图分类号：TE256

文献标识码：A

文章编号：1000-0747(2016)03-0462-07

DOI:10.11698/PED.2016.03.18

基金项目：国家自然科学基金项目（51274170）

第一作者简介：林元华（1971-），男，四川宜宾人，西南石油大学教授，主要从事油井管、油气钻井工艺方面的科研和教学工作。地址：四川省成都市新都区，西南石油大学材料科学与工程学院，邮政编码：610500。E-mail: yhlin28@163.com

收稿日期：2015-04-08 修回日期：2016-03-09