洪泛区河道行洪能力数值模拟研究
2016-07-06辽宁省丹东水文局辽宁丹东118000
吕 敏(辽宁省丹东水文局,辽宁丹东118000)
洪泛区河道行洪能力数值模拟研究
吕 敏
(辽宁省丹东水文局,辽宁丹东118000)
由于我国的防洪措施不完善,人口密度相对较大,洪水发生时会造成严重的损失。如何合理的对河道进行设计,计算河道的洪水水位,预测洪水的演进路线和破坏力,对抗洪抢险有着重要意义。随着数值模拟在水利工程中的应用,对水力特性研究和洪水演进提供了较好的模拟数据。以公路桥到水利枢纽间的44km河道为研究对象,首先建立了浅水运动控制方程,并对该方程进行离散化。随后采用MIKE11HD和HEC-RAS两种差分格式对洪泛区河道行洪能力进行数值模拟,分析了两种软件计算水位情况。研究表明:由于两种软件的水力半径不同,HEC-RAS软件的计算水位较高。
洪泛区;河道;行洪能力;数值模拟
DOI:10.3969 /j.issn.1672-2469.2016.01.011
洪水是由于急剧降水、急骤冰雪融化、风暴引起的江河湖海水位迅速提升的水流现象。研究表明:洪水具有流量大、流速高、来势凶猛、破坏力强等特点。由于我国的防洪措施不完善,人口密度相对较大,洪水发生时会造成严重的损失。泄洪是水利建设中的重要技术问题,水利工程的修建势必引起河道水流特性的改变,如果不采取有效措施,将会冲刷下游河床,危及水利枢纽的安全。如何合理的对河道进行设计,计算河道的洪水水位,预测洪水的演进路线和破坏力,对抗洪抢险有着重要意义。
由于数值仿真较传统物理模型更为简单,修改模型十分方便。随着数值模拟在水利工程中的应用,对水力特性研究和洪水演进提供了较好的模拟数据。目前,国内外都会对洪泛区进行洪水风险分析,并对一定洪水位下的淹没面积进行数值计算。以公路桥到水利枢纽间的44km河道为研究对象,首先建立了浅水运动控制方程,并对该方程进行离散化。随后采用MIKE11HD和HEC-RAS两种差分格式对洪泛区河道行洪能力进行数值模拟,分析了两种格式计算水位情况。希望为今后的洪水水位计算提供参考。
1 浅水运动控制方程
在数值模拟普遍之前,计算河道行洪能力的方法主要有:水文学法、系统方法、水力学法。水文方法对初始条件的要求十分简单,仅需要洪水的测量数据,不需要河道的结构参数,应用最为广泛。系统学方法是将河道内的水流视为一个完整的系统,将进水量作为系统入口,出流量作为输出结构,河道则为系统的作用过程。水力学法主要依据圣维南定理得出,物理基础很强。上世纪50年代,计算水力学诞生,其将水力学和数值计算相结合,对流体力学的求解起到了很大的促进。
为了计算研究河道的行洪能力,首先建立了浅水运动控制方程,并对该方程进行离散化。浅水运动控制方程主要针对不可压、粘性流体,采用纳维斯-托克斯方程进行建模。由于浅水运动十分复杂,在进行建模时需满足以下假设:
(1)洪泛区河道的水体水平速度要比垂直速度大的多,因此忽略垂直方向的加速度,认为垂直方向的压强分布为静水压强分布。
(2)由于浅水运动中,水流的密度变化不大,较大的密度变化只在特殊情况出现,因此动量方程中认为密度恒定。
(3)在正常温度和压力下,流体的弹性模量基本恒定,忽略其压缩性,认为其为不可压流体。
由基本假设可知,流体速度沿垂向均匀分布,当水流在横向上分布均匀时,即可采用一维运动方程进行求解,将二维浅水运动控制方程沿着y轴积分,并按照河道宽度取平均值,即可得到一维浅水运动控制方程。
连续性方程:
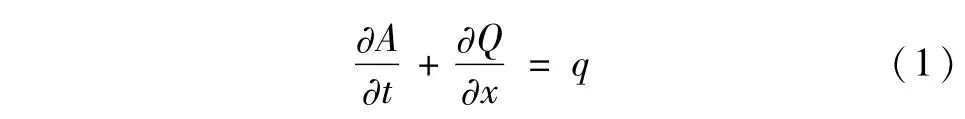
动量方程:
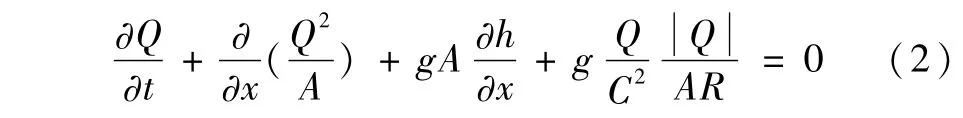
其中:Q为流量值;A为河道截面积;x为横坐标;t为时间坐标;h为洪水位;q为旁侧入流流量;C、n为系数;R为水力半径。
MIKE11HD差分格式采用Q和H交叉计算的方法对一维浅水运动控制方程进行离散,六点隐式方法进行离散,该方法将H和Q进行交替计算,计算示意图见图1。

图1 MIKE11HD差分格式离散方法
HEC-RAS差分格式采用四点隐式方法进行离散,这种方法主要针对变量f,在因变量一阶偏微分方程的基础上,采用相邻点间加权平均离散方法,对相同时间层t的偏微分取j和j+1两个插商值,对相邻点x的偏微分取t和t+1插商进行平均。HEC-RAS差分格式离散方法见图2。

图2 HEC-RAS差分格式离散方法
2 行洪能力数值模拟
2.1 模型建立
在模拟之前首先建立数学模型。在模型建立前,首先以河道参数为计算基础,结合圣维南定理,确定相应的边界条件和初始条件。网格划分在GAMBIT软件中完成,并设置好边界条件和入口参数,为了保证计算精度,对网格进行加密处理,横断面间距为0.1km。河道的地形数据可以反映出沿程断面的变化规律,据此得出计算区域水流量和水位的关系。计算采用分离式求解器,并进行压力场与速度场的耦合。
2.2 求解结果
采用两种差分格式对计算河道内的渡河大桥进行行洪计算,两种格式的计算方法都建立在能量方程的基础上。采用半经验公式计算渡河大桥桥墩处的水位壅水情况,并与两种差分格式的计算结果进行对比。HEC-RAS差分格式计算结果见图3,MIKE11HD差分格式计算结果见图4。

图3 HEC-RAS差分格式计算结果

图4 MIKE11HD差分格式计算结果
由数值计算结果可知,MIKE11HD格式计算的壅水高度为0.038m;HEC-RAS差分格式计算的壅水高度为0.041m;Henderson半经验公式计算的壅水高度为0.027m;无坎宽顶堰半经验公式计算的壅水高度为0.03m;规范公式计算的壅水高度为0.017m。两种计算值与半经验公式结果相近,分析产生误差的原因,半经验公式计
算时采用的比降为全局比降,而数值计算中采用的比降与每个断面的水位高程、河底深度均相关,因此计算出的壅水高度较大。
为了便于对比两种差分格式的计算误差,图5给出了44km河道的两种模型计算结果对比。

图5 两种模型计算结果对比
由图5可以看出,两种差分格式得出的计算结果基本一致,只是在中部有点偏差。但是当计算距离大于35km后,HEC-RAS差分格式的计算结果明显大于MIKE11HD差分格式,最大偏差值为0.55m。分析产生偏差的原因:两种格式的水力半径不同,HEC-RAS软件的计算水位较高。
3 结语
洪水具有流量大、流速高、来势凶猛、破坏力强等特点。水利工程的修建势必引起河道水流特性的改变,如果不采取有效措施,将会冲刷下游河床,危及水利枢纽的安全。通过建立浅水运动控制方程,并对该方程进行离散化,采用MIKE11HD和HEC-RAS两种差分格式对洪泛区河道行洪能力进行数值模拟。研究表明:
(1)两种计算值与半经验公式结果相近,但半经验公式计算时采用的比降为全局比降,而数值计算中采用的比降与每个断面的水位高程、河底深度均相关,因此计算出的壅水高度较大。
(2)两种差分格式得出的计算结果基本一致,但是当计算距离大于35km后,HEC-RAS格式结果明显大于MIKE11HD格式,这是由于两种格式的水力半径不同。
[1]张验科,王丽萍,刘方,等.模拟最大熵法及其在河道行洪风险计算中的应用[J].中国农村水利水电,2011(02):121-124.
[2]苏崇峰.沂河华沂至铁路桥段河道治理方案研究[J].水利技术监督,2011(04):51-53 +65.
[3]姜树海.基于随机微分方程的河道行洪风险分析[J].水利水运科学研究,1995(02):127-137.
[4]郭梦京,李婧,周孝德,等.水动力模拟在渣场河道行洪分析中的应用[J].水土保持通报,2013(02):156-159.
[5]杨婷.浅析城市水土流失与行洪排涝——以珠江三角洲城市为例[J].水利技术监督,2013(04):31-32 +44.
[6]李计龙.玛纳斯河河道采砂规划分析[J].水利规划与设计,2015(03):11-12.
[7]余彦群,杨晓梅.淮河干流王家坝至临淮岗段河道治理[J].水利规划与设计,2013(11):62-65.
[8]贺芳丁,冯毅,张涛.尚庄水库除险加固工程溢洪道设计方案分析[J].水利技术监督,2011(05):45-47.
TV135
A
1672-2469(2016)01-0033-02
2015-06-19
吕 敏(1963年—),女,工程师。
